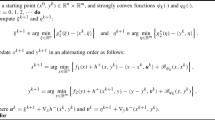Abstract
In this paper, we consider a partial sparse and partial group sparse optimization problem, where the loss function is a continuously differentiable function (possibly nonconvex), and the penalty term consists of two parts associated with sparsity and group sparsity. The first part is the \(\ell _0\) norm of \(\textbf{x}\), the second part is the \(\ell _{2,0}\) norm of \(\textbf{y}\), i.e., \(\lambda _1\Vert \textbf{x}\Vert _0+\lambda _2\Vert \textbf{y}\Vert _{2,0}\), where \((\textbf{x,y})\in \mathbb {R}^{n+m}\) is the decision variable. We give a continuous relaxation model of the above original problem, where the two parts of the penalty term are relaxed by Capped-\(\ell _1\) of \(\textbf{x}\) and group Capped-\(\ell _1\) of \(\textbf{y}\) respectively. Firstly, we define two kinds of first-order stationary points of the relaxation model. Based on the lower bound property of d-stationary points of the relaxation model, we establish the equivalence of solutions of the original problem and the relaxation model, which provides a theoretical basis for solving the original problem via solving the relaxation problem. Secondly, we propose an alternating proximal gradient (APG) algorithm to solve the relaxation model, and prove that the whole sequence of the APG algorithm converges to a critical point under some mild conditions. Finally, numerical experiments on simulated data and multichannel image as well as comparison with some state-of-art algorithms are presented to illustrate the effectiveness and robustness of the proposed algorithm for partial sparse and partial group sparse optimization problem.




Similar content being viewed by others
Data Availability
All data included in this manuscript are available upon reasonable request by contact with the corresponding author.
References
Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. 116(1–2), 5–16 (2009)
Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka-Łojasiewicz inequality. Math. Oper. Res. 35(2), 438–457 (2010)
Bian, W., Chen, X.: A smoothing proximal gradient algorithm for nonsmooth convex regression with cardinality penalty. SIAM J. Numer. Anal. 58(1), 858–883 (2020)
Bian, W., Chen, X.: Optimality and complexity for constrained optimization problems with nonconvex regularization. Math. Oper. Res. 42(4), 1063–1084 (2017)
Blumensath, T.: Compressed sensing with nonlinear observations and related nonlinear optimization problems. IEEE Trans. Inf. Theory 59(6), 3466–3474 (2013)
Bolte, J., Daniilidis, A., Lewis, A.: The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 17(4), 1205–1223 (2007)
Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146(1–2), 459–494 (2014)
Breheny, P., Huang, J.: Group descent algorithms for nonconvex penalized linear and logistic regression models with grouped predictors. Stat. Comput. 25(2), 173–187 (2015)
Chandran, M.: Analysis of Bayesian Group-Lasso in Regression Models. University of Florida, Gainesville (2011)
Chartrand, R.: Exact reconstruction of sparse signals via nonconvex minimization. IEEE Signal Process. Lett. 14(10), 707–710 (2007)
Chen, X., Pan, L., Xiu, N.: Solution sets of three sparse optimization problems for multivariate regression. J. Global Optim. 87(2–4), 347–371 (2023)
Chen, X., Xu, F., Ye, Y.: Lower bound theory of nonzero entries in solutions of \(\ell _2\)-\(\ell _p\) minimization. SIAM J. Sci. Comput. 32(5), 2832–2852 (2010)
Clarke, F.H.: Optimization and nonsmooth analysis. SIAM J. Control Optim. (1990)
Elad, M., Figueiredo, M.A.T., Ma, Y.: On the role of sparse and redundant representations in image processing. Proc. IEEE 98(6), 972–982 (2010)
Fan, J., Li, R.: Statistical challenges with high dimensionality: feature selection in knowledge discovery. Proc. Int. Congr. Math. 3, 595–622 (2006)
Fan, J., Li, R.: Variable selection via nonconvave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96(456), 1348–1360 (2001)
Feng, X., Yan, S., Wu, C.: The \(\ell _{2, q}\) regularized group sparse optimization: lower bound theory, recovery bound and algorithms. Appl. Comput. Harmon. Anal. 49(2), 381–414 (2020)
Gong, P., Zhang, C., Lu, Z., Huang, J., Ye, J.: A general iterative shrinkage and thresholding algorithm for non-convex regularized optimization problems. In: Proceedings of the 30th International Conference on International Conference on Machine Learning (ICML’13), vol. 28(2), pp. 37–45 (2013)
Huang, J., Ma, S., Xie, H., Zhang, C.H.: A group bridge approach for variable selection. Biometrika 96(2), 339–355 (2009)
Huang, J., Zhang, T.: The benefit of group sparsity. Ann. Stat. 38(4), 1978–2004 (2010)
Hu, Y., Li, C., Meng, K., Qin, J., Yang, X.: Group sparse optimization via \(\ell _{p, q}\) regularization. J. Mach. Learn. Res. 18(30), 1–52 (2017)
Jiang, D.: Concave Selection in Generalized Linear Models. University of Iowa, Iowa City (2012)
Jiao, Y., Jin, B., Lu, X.: Group sparse recovery via the \(\ell _{0}(\ell _2)\) penalty: theory and algorithm. IEEE Trans. Signal Process. 65(4), 998–1012 (2017)
Le Thi, H.A., Pham Dinh, T., Le, H.M., Vo, X.T.: DC approximation approaches for sparse optimization. Eur. J. Oper. Res. 244(1), 26–46 (2015)
Li, W., Bian, W., Toh, K.C.: DC algorithms for a class of sparse group \(\ell _0 \) regularized optimization problems. SIAM J. Optim. 32(3), 1614–1641 (2022)
Nikolova, M., Tan, P.: Alternating structure-adapted proximal gradient descent for nonconvex nonsmooth block-regularized problems. SIAM J. Optim. 29(3), 2053–2078 (2019)
Ong, C.S., An, L.T.H.: Learning sparse classifiers with difference of convex functions algorithms. Optim. Methods Softw. 28(4), 830–854 (2013)
Pang, J.S., Razaviyayn, M., Alvarado, A.: Computing B-stationary points of nonsmooth DC programs. Math. Oper. Res. 42(1), 95–118 (2017)
Pan, L., Chen, X.: Group sparse optimization for images recovery using capped folded concave functions. SIAM J. Imag. Sci. 14(1), 1–25 (2021)
Peng, D., Chen, X.: Computation of second-order directional stationary points for group sparse optimization. Optim. Methods Softw. 35(2), 348–376 (2020)
Phan, D.N., Le Thi, H.A.: Group variable selection via \(\ell _{p,0}\) regularization and application to optimal scoring. Neural Netw. 118, 220–234 (2019)
Raman, S., Fuchs, T.J., Wild, P.J.: The Bayesian group-Lasso for analyzing contingency tables. In: Proceedings of the 26th Annual International Conference on Machine Learning, pp. 881–888 (2009)
Rockafellar, R.T., Wets, R.J.B.: Variational Analysis. Springer, Berlin (2009)
Shen, H., Peng, D., Zhang, X.: Smoothing composite proximal gradient algorithm for sparse group Lasso problems with nonsmooth loss functions. J. Appl. Math. Comput. (2024). https://doi.org/10.1007/s12190-024-02034-2
Simon, N., Friedman, J., Hastie, T., Tibshirani, R.: A sparse-group Lasso. J. Comput. Graph. Stat. 22(2), 231–245 (2013)
Soubies, E., Blanc-Féraud, L., Aubert, G.: A continuous exact \(\ell _0\) penalty (Capped-\(\ell _0\)) for least squares regularized problem. SIAM J. Imaging Sci. 8(3), 1574–1606 (2015)
Soubies, E., Blanc-Féraud, L., Aubert, G.: A unified view of exact continuous penalties for \(\ell _2-\ell _0\) minimization. SIAM J. Optim. 27(3), 2034–2060 (2017)
Van den Berg, E., Friedlander, M.P.: Probing the pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 31(2), 890–912 (2009)
Wang, L., Chen, G., Li, H.: Group SCAD regression analysis for microarray time course gene expression data. Bioinformatics 23(12), 1486–1494 (2007)
Yuan, M., Lin, Y.: Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 68(1), 49–67 (2006)
Zhang, C.H.: Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 38(2), 894–942 (2010)
Zhang, T.: Analysis of multi-stage convex relaxation for sparse regularization. J. Mach. Learn. Res. 11(35), 1081–1107 (2010)
Zhang, X., Peng, D.: Solving constrained nonsmooth group sparse optimization via group Capped-\(\ell _1\) relaxation and group smoothing proximal gradient algorithm. Comput. Optim. Appl. 83(3), 801–844 (2022)
Zhang, X., Peng, D., Su, Y.: A singular value shrinkage thresholding algorithm for folded concave penalized low-rank matrix optimization problems. J. Global Optim. 88(2), 485–508 (2024)
Zhang, Y., Zhang, N., Sun, D.: An efficient Hessian based algorithm for solving large-scale sparse group Lasso problems. Math. Program. 179(1), 223–263 (2020)
Zhao, P., Rocha, G., Yu, B.: The composite absolute penalties family for grouped and hierarchical variable selection. Ann. Stat. 37(6A), 3468–3497 (2009)
Zhou, Y., Han, J., Yuan, X.: Inverse sparse group Lasso model for robust object tracking. IEEE Trans. Multimed. 19(8), 1798–1810 (2017)
Acknowledgements
This work is supported by the National Natural Science Foundation of China (12261020), the Guizhou Provincial Science and Technology Program (ZK[2021]009), the Foundation for Selected Excellent Project of Guizhou Province for High-level Talents Back from Overseas ([2018]03), and the Research Foundation for Postgraduates of Guizhou Province (YJSCXJH[2020]085).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wu, Q., Peng, D. & Zhang, X. Continuous Exact Relaxation and Alternating Proximal Gradient Algorithm for Partial Sparse and Partial Group Sparse Optimization Problems. J Sci Comput 100, 20 (2024). https://doi.org/10.1007/s10915-024-02584-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-024-02584-4
Keywords
- Partial sparse and partial group sparse optimization problem
- Continuous exact relaxation
- Stationary point
- Alternating proximal gradient algorithm
- The whole sequence convergence