Skip to main content
Springer Nature Link
Log in

Analysis of the Local Discontinuous Galerkin Method with Generalized Numerical Fluxes for One-Dimensional Nonlinear Fourth-Order Time-Dependent Problems

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

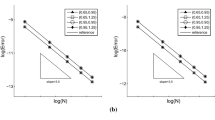
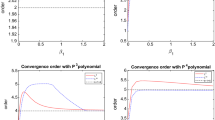
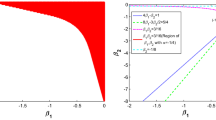
In this paper, we study the local discontinuous Galerkin method with generalized numerical fluxes for one-dimensional nonlinear time-dependent fourth-order equations. The \(L^2\) stability and optimal error estimates of order \(k+1\) are obtained with piecewise polynomials of degree \(k \ge 1\). The numerical flux of the nonlinear convection term is the generalized local Lax–Friedrichs flux, and the generalized alternating fluxes are adopted for the fourth- and second-order terms. The adjustable numerical viscosity of these fluxes is beneficial for long time simulations with a slower error growth. A proper numerical initial condition is designed based on a modified projection of the third-order derivative. By using the generalized Gauss–Radau projections, together with sharp bounds of nonlinear and jump terms, optimal error estimates are derived. The results are extended to equations with an additional dispersion term and mixed boundary conditions. Examples including Dirichlet as well as generalized Dirichlet boundary conditions, singularly perturbed problems and two-dimensional problems are also numerically investigated, indicating that the theoretical results hold for more general cases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Data Availability

No datasets were generated or analyzed during the current study. The codes required during the algorithm implementation are available from the corresponding author on reasonable request.

References

  1. Ai, J., Xu, Y., Shu, C.W., Zhang, Q.: \(L^2\) error estimate to smooth solutions of high order Runge–Kutta discontinuous Galerkin method for scalar nonlinear conservation laws with and without sonic points. SIAM J. Numer. Anal. 60(4), 1741–1773 (2022). https://doi.org/10.1137/21M1435495

    Article  MathSciNet  MATH  Google Scholar 

  2. Brenner, S.C.: Poincaré-Friedrichs inequalities for piecewise \(H^1\) functions. SIAM J. Numer. Anal. 41(1), 306–324 (2003). https://doi.org/10.1137/S0036142902401311

    Article  MathSciNet  MATH  Google Scholar 

  3. Brenner, S.C.: Discrete Sobolev and Poincaré inequalities for piecewise polynomial functions. Electron. Trans. Numer. Anal. 18, 42–48 (2004)

    MathSciNet  MATH  Google Scholar 

  4. Cheng, Y., Meng, X., Zhang, Q.: Application of generalized Gauss–Radau projections for the local discontinuous Galerkin method for linear convection-diffusion equations. Math. Comp. 86(305), 1233–1267 (2017). https://doi.org/10.1090/mcom/3141

    Article  MathSciNet  MATH  Google Scholar 

  5. Cheng, Y., Zhang, F., Zhang, Q.: Local analysis of local discontinuous Galerkin method for the time-dependent singularly perturbed problem. J. Sci. Comput. 63(2), 452–477 (2015). https://doi.org/10.1007/s10915-014-9901-6

    Article  MathSciNet  MATH  Google Scholar 

  6. Cockburn, B., Hou, S., Shu, C.W.: The Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV. The multidimensional case. Math. Comp. 54(190), 545–581 (1990). https://doi.org/10.2307/2008501

    Article  MathSciNet  MATH  Google Scholar 

  7. Cockburn, B., Shu, C.W.: TVB Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws. II. General framework. Math. Comp. 52(186), 411–435 (1989). https://doi.org/10.2307/2008474

    Article  MathSciNet  MATH  Google Scholar 

  8. Cockburn, B., Shu, C.W.: The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM J. Numer. Anal. 35(6), 2440–2463 (1998). https://doi.org/10.1137/S0036142997316712

    Article  MathSciNet  MATH  Google Scholar 

  9. Cockburn, B., Shu, C.W.: The Runge–Kutta discontinuous Galerkin method for conservation laws. V. Multidimensional systems. J. Comput. Phys. 141(2), 199–224 (1998) https://doi.org/10.1006/jcph.1998.5892

  10. Cueto-Felgueroso, L., Peraire, J.: A time-adaptive finite volume method for the Cahn–Hilliard and Kuramoto–Sivashinsky equations. J. Comput. Phys. 227(24), 9985–10017 (2008). https://doi.org/10.1016/j.jcp.2008.07.024

    Article  MathSciNet  MATH  Google Scholar 

  11. Dee, G.T., van Saarloos, W.: Bistable systems with propagating fronts leading to pattern formation. Phys. Rev. Lett. 60(25), 2641–2644 (1988)

    Article  MATH  Google Scholar 

  12. Dong, B., Shu, C.W.: Analysis of a local discontinuous Galerkin method for linear time-dependent fourth-order problems. SIAM J. Numer. Anal. 47(5), 3240–3268 (2009). https://doi.org/10.1137/080737472

    Article  MathSciNet  MATH  Google Scholar 

  13. Emmerich, H., Löwen, H., Wittkowski, R., Gruhn, T., Tóth, G.I., Tegze, G., Gránásy, L.: Phase-field-crystal models for condensed matter dynamics on atomic length and diffusive time scales: An overview. Adv. Phys. 61(6), 665–743 (2012)

    Article  MATH  Google Scholar 

  14. Fu, F., Shu, C.W., Tao, Q., Wu, B.: Analysis of the boundary conditions for the ultraweak-local discontinuous Galerkin method of time-dependent linear fourth-order problems. Math. Comp. 94(351), 123–158 (2025). https://doi.org/10.1090/mcom/3955

    Article  MathSciNet  MATH  Google Scholar 

  15. Gajardo, D., Mercado, A., Muñoz, J.C.: Identification of the anti-diffusion coefficient for the linear Kuramoto–Sivashinsky equation. J. Math. Anal. Appl. (2021). https://doi.org/10.1016/j.jmaa.2020.124747

    Article  MathSciNet  MATH  Google Scholar 

  16. Ilati, M., Dehghan, M.: Direct local boundary integral equation method for numerical solution of extended Fisher–Kolmogorov equation. Eng. Comput. 34, 203–213 (2018)

    Article  MATH  Google Scholar 

  17. Ji, L., Xu, Y.: Optimal error estimates of the local discontinuous Galerkin method for Willmore flow of graphs on Cartesian meshes. Int. J. Numer. Anal. Model. 8(2), 252–283 (2011)

    MathSciNet  MATH  Google Scholar 

  18. Kassam, A.K., Trefethen, L.N.: Fourth-order time-stepping for stiff PDEs. SIAM J. Sci. Comput. 26(4), 1214–1233 (2005). https://doi.org/10.1137/S1064827502410633

    Article  MathSciNet  MATH  Google Scholar 

  19. Kollem, S., Reddy, K.R.L., Rao, D.S.: Denoising and segmentation of MR images using fourth order nonlinear adaptive PDE and new convergent clustering. Int. J. Imaging Syst. Technol. 29(3), 195–209 (2019)

    Article  MATH  Google Scholar 

  20. Kuramoto, Y.: Diffusion-induced chaos in reaction systems. Prog. Theor. Phys. Supp. 64, 346–367 (1978)

    Article  MATH  Google Scholar 

  21. Li, J., Zhang, D., Meng, X., Wu, B.: Analysis of local discontinuous Galerkin methods with generalized numerical fluxes for linearized KdV equations. Math. Comp. 89(325), 2085–2111 (2020). https://doi.org/10.1090/mcom/3550

    Article  MathSciNet  MATH  Google Scholar 

  22. Li, J., Zhang, D., Meng, X., Wu, B., Zhang, Q.: Discontinuous Galerkin methods for nonlinear scalar conservation laws: Generalized local Lax–Friedrichs numerical fluxes. SIAM J. Numer. Anal. 58(1), 1–20 (2020). https://doi.org/10.1137/19M1243798

    Article  MathSciNet  MATH  Google Scholar 

  23. Liu, Y., Tao, Q., Shu, C.W.: Analysis of optimal superconvergence of an ultraweak-local discontinuous Galerkin method for a time dependent fourth-order equation. ESAIM Math. Model. Numer. Anal. 54(6), 1797–1820 (2020). https://doi.org/10.1051/m2an/2020023

    Article  MathSciNet  MATH  Google Scholar 

  24. Meng, X., Shu, C.W., Wu, B.: Optimal error estimates for discontinuous Galerkin methods based on upwind-biased fluxes for linear hyperbolic equations. Math. Comp. 85(299), 1225–1261 (2016). https://doi.org/10.1090/mcom/3022

    Article  MathSciNet  MATH  Google Scholar 

  25. Narendranath, A.D.: Recurrence quantification analysis: Nonlinear wave dynamics in the Kuramoto–Sivashinsky equation, Response of the Tri-pendulum and FlanSea WEC and Extreme Events. In: OCEANS 2018 MTS/IEEE Charleston, pp. 1–10. IEEE (2018)

  26. Reed, W.H., Hill, T.R.: Triangular mesh methods for the neutron transport equation. Technical Report LA-UR-73-479, Los Alamos Scientific Laboratory, Los Alamos, NM (1973)

  27. Shu, C.W.: Discontinuous Galerkin methods for time-dependent convection dominated problems: basics, recent developments and comparison with other methods. In: Building bridges: connections and challenges in modern approaches to numerical partial differential equations, Lect. Notes Comput. Sci. Eng., vol. 114, pp. 369–397. Springer, [Cham] (2016)

  28. Sivashinsky, G.I.: Nonlinear analysis of hydrodynamic instability in laminar flames. I. Derivation of basic equations. Acta Astronaut. 4(11), 1177–1206 (1977). https://doi.org/10.1016/0094-5765(77)90096-0

    Article  MathSciNet  MATH  Google Scholar 

  29. Tan, M., Cheng, J., Shu, C.W.: Stability of high order finite difference and local discontinuous Galerkin schemes with explicit-implicit-null time-marching for high order dissipative and dispersive equations. J. Comput. Phys. 464, 25 (2022). https://doi.org/10.1016/j.jcp.2022.111314

    Article  MathSciNet  MATH  Google Scholar 

  30. Toro, E.F.: Riemann Solvers and Numerical Methods for Fluid Dynamics. A Practical Introduction, 3rd edn. Springer, Berlin (2009). https://doi.org/10.1007/b79761

    Book  MATH  Google Scholar 

  31. Wang, H., Zhang, Q., Shu, C.W.: Stability analysis and error estimates of local discontinuous Galerkin methods with implicit-explicit time-marching for the time-dependent fourth order PDEs. ESAIM Math. Model. Numer. Anal. 51(5), 1931–1955 (2017). https://doi.org/10.1051/m2an/2017017

    Article  MathSciNet  MATH  Google Scholar 

  32. Wang, H., Zhang, Q., Shu, C.W.: Correction to: Implicit-explicit local discontinuous Galerkin methods with generalized alternating numerical fluxes for convection-diffusion problems. J. Sci. Comput. (2024). https://doi.org/10.1007/s10915-024-02697-w

    Article  MathSciNet  MATH  Google Scholar 

  33. Xu, Y., Shu, C.W.: Local discontinuous Galerkin methods for the Kuramoto–Sivashinsky equations and the Ito-type coupled KdV equations. Comput. Methods Appl. Mech. Engrg. 195(25–28), 3430–3447 (2006). https://doi.org/10.1016/j.cma.2005.06.021

    Article  MathSciNet  MATH  Google Scholar 

  34. Yan, J., Shu, C.W.: A local discontinuous Galerkin method for KdV type equations. SIAM J. Numer. Anal. 40(2), 769–791 (2002). https://doi.org/10.1137/S0036142901390378

    Article  MathSciNet  MATH  Google Scholar 

  35. Yang, Y., Shu, C.W.: Analysis of optimal superconvergence of discontinuous Galerkin method for linear hyperbolic equations. SIAM J. Numer. Anal. 50(6), 3110–3133 (2012). https://doi.org/10.1137/110857647

    Article  MathSciNet  MATH  Google Scholar 

  36. Zhang, H., Meng, X., Zhang, D., Wu, B.: Optimal error estimates of the local discontinuous Galerkin method with generalized numerical fluxes for one-dimensional KdV type equations. J. Comput. Math. 43(1), 63–88 (2025). https://doi.org/10.4208/jcm.2307-m2022-0278

    Article  MathSciNet  MATH  Google Scholar 

  37. Zhang, L.: A local energy-based discontinuous Galerkin method for fourth-order semilinear wave equations. IMA J. Numer. Anal. 44(5), 2793–2820 (2024). https://doi.org/10.1093/imanum/drad076

    Article  MathSciNet  MATH  Google Scholar 

  38. Zhang, Q., Shu, C.W.: Stability analysis and a priori error estimates of the third order explicit Runge–Kutta discontinuous Galerkin method for scalar conservation laws. SIAM J. Numer. Anal. 48(3), 1038–1063 (2010). https://doi.org/10.1137/090771363

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to anonymous reviewers for their valuable suggestions, which greatly improved the quality of the paper.

Funding

Xiong Meng was supported by NSFC Grants 12371365, 11971132, Natural Science Foundation of Heilongjiang Province Grant YQ2021A002, and the Fundamental Research Funds for the Central Universities Grant HIT.OCEF.2022031. Jia Li was supported by NSFC Grant 12101158 and the Fellowship of China Postdoctoral Science Foundation Grant 2021M701010.

Author information

Authors and Affiliations

  1. School of Mathematics, Harbin Institute of Technology, Harbin, 150001, Heilongjiang, China

    Linhui Li, Xiong Meng & Jia Li

Authors
  1. Linhui Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiong Meng
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jia Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xiong Meng.

Ethics declarations

Conflict of interest

The authors declare that they have no Conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, L., Meng, X. & Li, J. Analysis of the Local Discontinuous Galerkin Method with Generalized Numerical Fluxes for One-Dimensional Nonlinear Fourth-Order Time-Dependent Problems. J Sci Comput 102, 72 (2025). https://doi.org/10.1007/s10915-025-02800-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-025-02800-9

Keywords

Mathematics Subject Classification