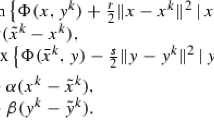Skip to main content
Springer Nature Link
Log in

Generalized Asymmetric Forward–Backward–Adjoint Algorithms for Convex–Concave Saddle-Point Problem

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

The convex–concave minimax problem, also known as the saddle-point problem, has been extensively studied from various aspects including the algorithm design, convergence condition and complexity. In this paper, we propose a generalized asymmetric forward–backward–adjoint algorithm (G-AFBA) to solve such a problem by utilizing both the proximal techniques and the extrapolation of primal-dual updates. Besides applying proximal primal-dual updates, G-AFBA enjoys a more relaxed convergence condition, namely, more flexible and possibly larger proximal stepsizes, which could result in significant improvements in numerical performance. We study the global convergence of G-AFBA as well as its sublinear convergence rate on both ergodic iterates and non-ergodic optimality error. The linear convergence rate of G-AFBA is also established under a calmness condition. By different ways of parameter and problem setting, we show that G-AFBA has close relationships with several well-established or new algorithms. We further propose an adaptive and a stochastic (inexact) versions of G-AFBA. Our numerical experiments on solving the robust principal component analysis problem and the 3D CT reconstruction problem indicate the efficiency of both the deterministic and stochastic versions of G-AFBA.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Notes

  1. Recently, its weak convergence was established in [2] when \(\alpha >1/2\) and \(\tau \sigma L<4/(1+2\alpha ).\)

  2. Note that (3.3) is equivalent to \( \theta (u)-\theta (\tilde{u}^{k})+\big \langle u-\tilde{u}^{k}, {\mathcal {J}}(\tilde{u}^{k})\big \rangle \ge (u-\tilde{u}^{k})^{\top }Q(u^{k}-\tilde{u}^{k})\).

References

  1. Arrow, K., Hurwicz, L., Uzawa, H.: Studies in Linear and Non-linear Programming, Stanford Mathematical Studies in the Social Sciences, vol. II. Stanford University Press, Stanford (1958)

    MATH  Google Scholar 

  2. Banert, S., Upadhyaya,M., Giselsson, P.: The Chambolle–Pock method converges weakly with \(\theta >1/2\) and \(\tau \sigma \Vert L\Vert ^2<4/(1+2\theta )\) (2023). arXiv:2309.03998v1

  3. Bai, J., Chang, X., Li, J., Xu, F.: Convergence revisit on generalized symmetric ADMM. Optimization 70, 149–168 (2021)

    MathSciNet  MATH  Google Scholar 

  4. Bai, J., Hager, W., Zhang, H.: An inexact accelerated stochastic ADMM for separable convex optimization. Comput. Optim. Appl. 81, 479–518 (2022)

    MathSciNet  MATH  Google Scholar 

  5. Bai, J., Jia, L., Peng, Z.: A new insight on augmented Lagrangian method with applications in machine learning. J. Sci. Comput. 99, 53 (2024)

    MathSciNet  MATH  Google Scholar 

  6. Bai, J., Bian, F., Chang, X., Du, L.: Accelerated stochastic Peaceman–Rachford method for empirical risk minimization. J. Oper. Res. Soc. China 11, 783–807 (2023)

    MathSciNet  MATH  Google Scholar 

  7. Bian, F., Liang, J., Zhang, X.: A stochastic alternating direction method of multipliers for non-smooth and non-convex optimization. Inverse Prob. 37, 075009 (2021)

    MathSciNet  MATH  Google Scholar 

  8. Candes, E., Li, X., Ma, Y., Wright, J.: Robust principal component analysis? J. ACM 58, 1–37 (2011)

    MathSciNet  MATH  Google Scholar 

  9. Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vision 40, 120–145 (2011)

    MathSciNet  MATH  Google Scholar 

  10. Chambolle, A., Pock, T.: On the ergodic convergence rates of a first-order primal-dual algorithm. Math. Program. 159, 253–287 (2016)

    MathSciNet  MATH  Google Scholar 

  11. Chambolle, A., Ehrhardt, M., Richtarik, P., Schonlieb, C.: Stochastic primal-dual hybrid gradient algorithm with arbitrary sampling and imaging applications. SIAM J. Optim. 28, 2783–2808 (2018)

    MathSciNet  MATH  Google Scholar 

  12. Chang, X., Yang, J., Zhang, H.: Golden ratio primal-dual algorithm with line search. SIAM J. Optim. 32, 1584–1613 (2022)

    MathSciNet  MATH  Google Scholar 

  13. Chandrasekaran, V., Sanghavi, S., Parrilo, P., Willsky, A.: Rank-sparsity incoherence for matrix decomposition. SIAM J. Optim. 21, 572–596 (2011)

    MathSciNet  MATH  Google Scholar 

  14. Condat, L.: A primal-dual splitting method for convex optimization involving Lipschitzian, proximable and linear composite terms. J. Optim. Theory Appl. 158, 460–479 (2013)

    MathSciNet  MATH  Google Scholar 

  15. Condat, L., Kitahara, D., Contreras, A., Hirabayashi, A.: Proximal splitting algorithms for convex optimization: a tour of recent advances, with new twists. SIAM Rev. 65, 375–435 (2023)

    MathSciNet  MATH  Google Scholar 

  16. Deng, W., Yin, W.: On the global and linear convergence of the generalized alternating direction method of multipliers. J. Sci. Comput. 66, 889–916 (2016)

    MathSciNet  MATH  Google Scholar 

  17. Eckstein, J., Bertsekas, D.: On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 55, 293–318 (1992)

    MathSciNet  MATH  Google Scholar 

  18. Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite-element approximations. Comput. Math. Appl. 2, 17–40 (1976)

    MATH  Google Scholar 

  19. Gao, H.: Fast parallel algorithms for the X-ray transform and its adjoint. Med. Phys. 39, 7110–7120 (2012)

    MATH  Google Scholar 

  20. Goldstein, T., Li, M., Yuan, X.: Adaptive primal-dual splitting methods for statistical learning and image processing. NeurIPS, pp. 2089–2097 (2015)

  21. Hayden, S., Stanley, O.: A low patch-rank interpretation of texture. SIAM J. Imaging Sci. 6, 226–262 (2013)

    MathSciNet  MATH  Google Scholar 

  22. He, B., Yuan, X.: On the \(o(1/n)\) convergence rate of the Douglas–Rachford alternating direction method. SIAM J. Numer. Anal. 50, 700–709 (2012)

    MathSciNet  MATH  Google Scholar 

  23. He, B., You, Y., Yuan, X.: On the convergence of primal-dual hybrid gradient algorithm. SIAM J. Imaging Sci. 7, 2526–2537 (2014)

    MathSciNet  MATH  Google Scholar 

  24. He, B., Ma, F., Xu, S., Yuan, X.: A generalized primal-dual algorithm with improved convergence condition for saddle point problems. SIAM J. Imaging Sci. 15, 1157–1183 (2022)

    MathSciNet  MATH  Google Scholar 

  25. He, B., Xu, S., Yuan, X.: On convergence of the Arrow–Hurwicz method for saddle point problems. J. Math. Imaging Vision 64, 662–671 (2022)

    MathSciNet  MATH  Google Scholar 

  26. He, X., Huang, N., Fang, Y.: Non-ergodic convergence rate of an inertial accelerated primal-dual algorithm for saddle point problems. Commun. Nonlinear Sci. Numer. Simulat. 140, 108289 (2024)

    MathSciNet  MATH  Google Scholar 

  27. Huang, F., Chen, S.: Mini-batch stochastic ADMMs for nonconvex nonsmooth optimization (2019). arXiv: 1802.03284

  28. Jiang, F., Cai, X., Wu, Z., Han, D.: Approximate first-order primal-dual algorithms for saddle point problems. Math. Comput. 90, 1227–1262 (2021)

    MathSciNet  MATH  Google Scholar 

  29. Jiang, F., Wu, Z., Cai, X., Zhang, H.: A first-order inexact primal-dual algorithm for a class of convex-concave saddle point problems. Numer. Algor. 88, 1109–1136 (2021)

    MathSciNet  MATH  Google Scholar 

  30. Jiang, F., Cai, X., Han, D.: Inexact asymmetric forward–backward–adjoint splitting algorithms for saddle point problems. Numer. Algor. 94, 479–509 (2023)

    MathSciNet  MATH  Google Scholar 

  31. Jiang, F., Zhang, Z., He, H.: Solving saddle point problems: a landscape of primal-dual algorithm with larger stepsizes. J. Glob. Optim. 85, 821–846 (2023)

    MathSciNet  MATH  Google Scholar 

  32. Korpelevič, G.: An extragradient method for finding saddle points and for other problems. Èkon. Mat. Metody 12, 747–756 (1976)

    MathSciNet  MATH  Google Scholar 

  33. Latafat, P., Patrinos, P.: Asymmetric forward–backward–adjoint splitting for solving monotone inclusions involving three operators. Comput. Optim. Appl. 68, 57–93 (2017)

    MathSciNet  MATH  Google Scholar 

  34. Li, Z., Yan, M.: New convergence analysis of a primal-dual algorithm with large stepsizes. Adv. Comput. Math. 47, 1–20 (2021)

    MathSciNet  MATH  Google Scholar 

  35. Lions, P., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)

    MathSciNet  MATH  Google Scholar 

  36. O’Connor, D., Vandenberghe, L.: On the equivalence of the primal-dual hybrid gradient method and Douglas–Rachford splitting. Math. Program. 179, 85–108 (2020)

    MathSciNet  MATH  Google Scholar 

  37. Polyak, B.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phy. 4, 1–17 (1964)

    MATH  Google Scholar 

  38. Rockafellar, R.: Convex Analysis. Princeton University Press, Princeton (2015)

    MATH  Google Scholar 

  39. Robinson, S.: Some Continuity Properties of Polyhedral Multifunctions. Mathematical Programming at Oberwolfach, pp. 206–214. Springer, Berlin (1981)

    MATH  Google Scholar 

  40. Sun, H., Tai, X., Yuan, J.: Efficient and convergent preconditioned ADMM for the Potts models. SIAM J. Sci. Comput. 43, B455–B478 (2021)

    MathSciNet  MATH  Google Scholar 

  41. Tao, M., Yuan, X.: Recovering low-rank and sparse components of matrices from incomplete and noisy observations. SIAM J. Optim. 21, 57–81 (2011)

    MathSciNet  MATH  Google Scholar 

  42. Vũ, B.: A splitting algorithm for dual monotone inclusions involving cocoercive operators. Adv. Comput. Math. 38, 667–681 (2013)

    MathSciNet  MATH  Google Scholar 

  43. Wang, N., Li, J.: A class of preconditioners based on symmetric-triangular decomposition and matrix splitting for generalized saddle point problems. IMA J. Numer. Anal. 43, 2998–3025 (2023)

    MathSciNet  MATH  Google Scholar 

  44. Xian, W., Huang, F., Zhang, Y., Huang, H.: A faster decentralized algorithm for nonconvex minimax problems. NeurIPS (2021). https://openreview.net/forum?id=rjIjkiyAJao

  45. Xu, S.: A dual-primal balanced augmented Lagrangian method for linearly constrained convex programming. J. Appl. Math. Comput. 69, 1015–1035 (2023)

    MathSciNet  MATH  Google Scholar 

  46. Xu, S.: A search direction inspired primal-dual method for saddle point problems. Optimization Online (2020). https://optimization-online.org/2019/11/7491/

  47. Xu, Z., Zhang, H., Xu, Y., Lan, G.: A unified single-loop alternating gradient projection algorithm for nonconvex-concave and convex-nonconcave minimax problems. Math. Program. 201, 635–706 (2023)

    MathSciNet  MATH  Google Scholar 

  48. Yang, J., Zhang, Y.: Alternating direction algorithms for \(\ell _1\)-problems in compressive sensing. SIAM J. Sci. Comput. 33, 250–278 (2011)

    MathSciNet  MATH  Google Scholar 

  49. Yang, L., Pong, T., Chen, X.: Alternating direction method of multipliers for a class of nonconvex and nonsmooth problems with applications to background/foreground extraction. SIAM J. Imaging Sci. 10, 74–110 (2017)

    MathSciNet  MATH  Google Scholar 

  50. Zhang, X., Burger, M., Osher, S.: A unified primal-dual algorithm framework based on Bregman iteration. J. Sci. Comput. 46, 20–46 (2011)

    MathSciNet  MATH  Google Scholar 

  51. Zhu, M., Chan, T.: An Efficient Primal-Dual Hybrid Gradient Algorithm for Total Variation Image Restoration, CAM Report 08-34. UCLA, Los Angeles, CA (2008)

    MATH  Google Scholar 

  52. Zhu, Y., Liu, D., Dinh, Q.: New primal-dual algorithms for a class of nonsmooth and nonlinear convex–concave minimax problems. SIAM J. Optim. 32, 2580–2611 (2022)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous referees for providing very constructive comments, which have significantly improved the quality of the paper.

Funding

This research was supported by the National Natural Science Foundation of China (12471298, 12171479), the Shaanxi Fundamental Science Research Project for Mathematics and Physics (23JSQ031), the National Social Science Fund of China (22BGL118), and the MOE Project of Key Research Institute of Humanities and Social Sciences (22JJD110001).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics & MOE Key Laboratory for Complexity Science in Aerospace, Northwestern Polytechnical University, Xi’an, 710129, China

    Jianchao Bai

  2. School of Mathematics and Statistics, Northwestern Polytechnical University & MIIT Key Laboratory of Dynamics and Control of Complex Systems, Xi’an, 710129, China

    Yang Chen

  3. Center for Applied Statistics, School of Statistics, Renmin University of China, Beijing, 100872, China

    Xue Yu

  4. Beijing Advanced Innovation Center for Future Blockchain and Privacy Computing, Beijing, 100191, China

    Xue Yu

  5. Department of Mathematics, Louisiana State University, Baton Rouge, LA, 70803-4918, USA

    Hongchao Zhang

Authors
  1. Jianchao Bai
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yang Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xue Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Hongchao Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Jianchao Bai or Yang Chen.

Ethics declarations

Conflict of interest

The authors have not disclosed any Conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bai, J., Chen, Y., Yu, X. et al. Generalized Asymmetric Forward–Backward–Adjoint Algorithms for Convex–Concave Saddle-Point Problem. J Sci Comput 102, 80 (2025). https://doi.org/10.1007/s10915-025-02802-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-025-02802-7

Keywords

Mathematics Subject Classification