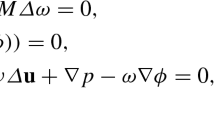1 Introduction

In this paper, we study the two-phase incompressible flow [1,2,3,4,5]:

$$\begin{aligned}&\partial _t\phi +\nabla \cdot ({{\textbf{u}}}\phi )=-{{\mathcal {M}}}\mu ,&\;\text {in}\; \Omega \times (0,T), \end{aligned}$$
(1.1a)
$$\begin{aligned}&\mu =\lambda \left( -\epsilon ^2\Delta \phi -f(\phi )+L(\phi (t))\right) ,&\;\text {in}\; \Omega \times (0,T), \end{aligned}$$
(1.1b)
$$\begin{aligned}&{{\textbf{u}}}_t+({{\textbf{u}}}\cdot \nabla ){{\textbf{u}}}-\nu \Delta {{\textbf{u}}}+\nabla p=\mu \nabla \phi ,&\;\text {in}\; \Omega \times (0,T), \end{aligned}$$
(1.1c)
$$\begin{aligned}&\nabla \cdot {{\textbf{u}}}=0,&\;\text {in}\; \Omega \times (0,T), \end{aligned}$$
(1.1d)

subject to the boundary condition

$$\begin{aligned} \frac{\partial \phi }{\partial {{\textbf{n}}}}|_{\partial \Omega }=0,\quad {{\textbf{u}}}|_{\partial \Omega }=0. \end{aligned}$$
(1.2)

Here, \(\Omega \subset {{\mathbb {R}}}^d\) is a smooth bounded domain, with the boundary \(\partial \Omega \). The unknowns in equations (1.1a)-(1.1d) are the phase function \(\phi \), the chemical potential \(\mu \), the velocity \({{\textbf{u}}}\), and the pressure p. The parameter \({{\mathcal {M}}}>0\) represents the mobility, while \(\epsilon >0\) is a small constant that controls the thickness of the diffuse interface. Additionally, \(\lambda >0\) is a constant related to the surface tension, and \(\nu \) denotes the fluid viscosity. The function f is the derivative of the configuration potential function F, i.e., \(f=-F'\), and the nonlocal term \(L(\phi (t))\) is the Lagrange multiplier, playing a crucial role in the elimination of the total mass variance \(|\Omega |\) (cf. [6]). A widely adopted choice for \(L(\phi (t))\) in (1.1b) is proposed in the following form:

$$\begin{aligned} L(\phi (t))=\frac{1}{|\Omega |}\int _\Omega f(\phi ({{\textbf{y}}},t))d{{\textbf{y}}},\; {{\textbf{x}}}\in \Omega . \end{aligned}$$
(1.3)

A variety of Allen-Cahn phase-field models have been widely utilized to simulate multi-component systems, including the multi-phase fluid flow, crystal growth, membranes for vesicles, and many others. In the conserved Allen-Cahn equation, a nonlocal term is proposed to eliminate the variance in mass caused by the nonlinear term, hence ensuring the preservation of total mass. Nevertheless, the conserved Allen-Cahn model becomes a highly complex system when coupled with the Navier–Stokes equations, thereby a significant challenge lies in designing the fully decoupled, linear, and maximum bound principle (MBP) preserving scheme that also satisfies the the unconditional energy dissipation law.

There are several effective methods for solving the incompressible Navier-Stokes equation and the conserved Allen-Cahn equation respectively. For the incompressible Navier–Stokes equation, Shen [7] proposed a first-order decoupled pressure-correction method and established rigorous error estimates. A unified approach on designing simple, efficient, and energy-stable time discretization schemes for the two-phase incompressible flow with matching or non-matching density has been presented in [8]. As for solving the phase-field model, various methods that preserve the energy dissipation law are used, such as linear stabilization [9], convex splitting method [10, 11], invariant energy quadratization [12, 13], and scalar auxiliary variable approach [14, 15].

We would like to point out that, in addition to energy stability, MBP is another crucial property of the conserved Allen-Cahn equation. A popular method preserving the MBP for the convective Allen-Cahn equation has been studied by using the upwind strategy for spatial discretization. In a previous study [16], a first-order numerical scheme was developed for the conserved Allen-Cahn equation, demonstrating the unconditional preservation of MBP by employing the upwind finite difference method. Recently, Cai et al. [17] extended this approach and constructed the first- and second-order in time unconditionally MBP-preserving upwind exponential time differencing (ETD) schemes. However, the upwind strategy only achieves first-order accuracy in space and requires strict CFL stability conditions, making it difficult to capture the dynamical interface behavior of the phase evolution in practice. Furthermore, in [18], the convective Allen-Cahn equation is split into a mass-conserving Allen-Cahn equation and a transport equation using the operator splitting approach. For the coupled conserved Allen-Cahn-Navier–Stokes equation, Huang, Lin, and Ardekani [19] developed a consistent and conservative scheme that ensures the mass and the momentum conservation while satisfying the energy law of the two-phase system. Moreover, Yang [5] constructed a fully decoupled scheme that is linear, unconditional energy stable, and second-order-in time accurate.

As far as we know, despite that a significant amount of work has been dedicated to the construction and analysis of the computational schemes to the conserved Allen-Cahn-Navier–Stokes (ACNS) system, there is still no fully decoupled, linear, high-order-in-time, unconditionally energy decay, and MBP preserving scheme. The objective of this study is to develop high-order and efficient numerical schemes for solving the hydrodynamically coupled mass-conserved Allen-Cahn phase-field model in a two-phase fluid flow system. The work presented in this paper is unique in the following aspects:

  • We construct first- and second-order in time, second-order in space, linear and fully decoupled schemes for the conserved ACNS model, ensuring unconditional energy stable through on the generalized stabilized exponential scalar auxiliary variable approach [20, 21].

  • The MBP properties of the Allen-Cahn equation with multipliers (1.3) under different potential function \(F(\phi )\) are rigorously proved. The main innovation of the proof is treating the nonlocal equation as a semi-linear parabolic equation with given coefficients, allowing us to utilize the strong maximum (comparison) principle and Hopf’s boundary point lemma for the parabolic equations and the special properties of the energy. This proof is quite concise, robust, and can be easily extended to a broader range of multipliers.

  • We derive the corresponding MBP for the developed first- and second-order numerical schemes in time based on the second-order MAC scheme in space rigorously. By establishing a unified framework under some reasonable assumptions [22, 23], we prove that the second-order spatial central difference method can still preserves the MBP.

To the best of the authors’ knowledge, this is the first linear, second-order accuracy in space and time, energy decay, and MBP-preserving numerical scheme for a two-phase fluid flow system.

The rest of this paper is organized as follows. In Sect. 2, we present some preliminaries and show the maximum bound principle for the nonlocal ACNS model and introduce some notations for the discretized problem. In Sect. 3, we propose the first- and second-order stabilized generalized exponential scalar auxiliary variable schemes, demonstrating their adherence to the unconditional energy dissipation law and the MBP. Numerical experiments are carried out to validate the theoretical results and demonstrate the performance of the proposed schemes in Sect. 4. Finally, some concluding remarks are given in Sect. 5.

2 The Problem Description and Notations

In this section, we first derive the energy dissipation law and the maximum bound principle (MBP) [24, 25] for the ACNS model (1.1). Following that, some preliminaries and notations will be presented below, which will be utilized throughout the paper.

The ACNS Eq. (1.1) with a nonlocal constraint satisfies an energy dissipation law. Indeed, taking the inner products of (1.1a) with \(\mu \), (1.1b) with \(\partial _t \phi \), and (1.1c) with \({{\textbf{u}}}\) respectively, summing them up yields the following energy dissipation law

$$\begin{aligned} \frac{d}{dt}{{\mathcal {E}}}(\phi ,{{\textbf{u}}})=-\int _\Omega {{\mathcal {M}}}|\mu |^2+\nu |\nabla {{\textbf{u}}}|^2d{{\textbf{x}}}, \end{aligned}$$

where

$$\begin{aligned} {{\mathcal {E}}}(\phi ,{{\textbf{u}}})=\int _\Omega \left( \lambda \left( \frac{\epsilon ^2}{2}|\nabla \phi |^2+F(\phi )\right) +\frac{1}{2}|{{\textbf{u}}}|^2\right) d{{\textbf{x}}}. \end{aligned}$$

We impose the following assumption on f, which will be used in establishing the MBP for (1.1) with \(L(\phi )\) given in (1.3); see Proposition 2.1.

Assumption 1

The function \(f: {{\mathbb {R}}} \rightarrow {{\mathbb {R}}}\) is continuously differentiable and there exists some \(\beta >0\) such that

$$\begin{aligned} f(\beta )\le f(x)\le f(-\beta ),\quad -\beta \le x\le \beta . \end{aligned}$$
(2.4)

We consider two common forms of the function \(F(\phi )\) used in phase-field modelling. The first one is the double-well structure, which can be expressed as

$$\begin{aligned} F(\phi )=\frac{1}{4}(\phi ^2-1)^2. \end{aligned}$$
(2.5)

The second form is the Flory-Huggins potential function, given by

$$\begin{aligned} F(\phi )=\frac{\theta }{2}[(1+\phi )\ln (1+\phi )+(1-\phi )\ln (1-\phi )] - \frac{\theta _c}{2}\phi ^2, \end{aligned}$$
(2.6)

where \(0<\theta <\theta _c\).

Given a terminal time \(T > 0\), we can deduce that the ACNS Eq. (1.1) satisfies the MBP under Assumption 1. We note that the MBP holds with different values of the maximum bounds depending on the choice of the function F in \(L(\phi (t))\) in (1.3).

Proposition 2.1

Let \({{\textbf{u}}}\in C([0,T]; [C^1(\Omega )]^d)\) and \(\phi \in C^1([0,T];C^2({\Omega }))\) be the solution to model (1.1) with \(L(\phi (t))\) given by (1.3). Suppose that f satisfies Assumption 1. Then the MBP holds, precisely, if the initial data satisfies \(\Vert \phi _0\Vert _\infty < \beta \), where \(\beta \) is determined by (2.4), then for any \(t\in [0,T]\), we have

$$\begin{aligned} \Vert \phi (\cdot , t)\Vert _\infty \le \beta . \end{aligned}$$

Proof

Let \(L(t)=\frac{1}{|\Omega |}\int _\Omega f(\phi ({{\textbf{y}}},t))d{{\textbf{y}}}.\) We then consider the following operator

$$\begin{aligned} {{\mathcal {S}}}(h):=\partial _th+\nabla \cdot ({{\textbf{u}}}h)+\lambda {{\mathcal {M}}}(-\epsilon ^2\Delta h-f(h) ). \end{aligned}$$

Obviously, \({{\mathcal {S}}}(\phi )(x,t)=-\lambda {{\mathcal {M}}} L(t)\). Moreover, we define

$$\begin{aligned} t^*=\sup \{0\le t\le T; \sup \limits _{0\le s\le t}||\phi (\cdot ,s)||_{L^{\infty }({\bar{\Omega }})}\le \beta \}. \end{aligned}$$

Then direct calculations together with (1.1d), i.e., \(\nabla \cdot {{\textbf{u}}}=0\) and (2.4) the assumption on f show that on \([0,t^*]\times {\bar{\Omega }}\), we have

$$\begin{aligned} \begin{aligned} {{\mathcal {S}}}(\beta ) = -\lambda {{\mathcal {M}}} f(\beta )\ge -\lambda {{\mathcal {M}}} L(t) = {{\mathcal {S}}}(\phi ),~ {{\mathcal {S}}}(-\beta ) = - \lambda {{\mathcal {M}}} f(-\beta )\le -\lambda {{\mathcal {M}}} L(t) = {{\mathcal {S}}}(\phi ). \end{aligned} \end{aligned}$$

The comparison principle [26] indicates that we only have three cases

$$\begin{aligned} -\beta<\phi (\cdot ,t^*)<\beta ~\text {on}\ {\Omega } \text { or } \phi (\cdot ,t^*)\equiv \beta ~\text {on}\ \Omega , \text { or } \phi (\cdot ,t^*)\equiv -\beta ~\text {on}\ \Omega . \end{aligned}$$
(2.7)

In the last two cases, by the uniqueness of the solution, we would have \(\phi ({{\textbf{x}}},t)\equiv \beta \), or \(\phi ({{\textbf{x}}},t)\equiv - \beta \) for \(t\in [t^*,T]\), since \(\phi ({{\textbf{x}}},t)\equiv \pm \beta \) for \(t\in [t^*,T]\) is another solution to (1.1) with \(\phi (x,t^*)=\pm \beta \). This contradicts the definition of \(t^*\) unless \(t^*=T\). Hence, we may assume \(-\beta<\phi (\cdot ,t^*)<\beta \) on \({\Omega }\). We further claim that

$$\begin{aligned} -\beta<\phi (\cdot ,t^*)<\beta ~\text {on}\ {\bar{\Omega }}. \end{aligned}$$
(2.8)

Otherwise, we have for some \(x\in \partial \Omega \) such that \(\phi (x,t^*)= \beta \text { or } \phi (x,t^*)= -\beta \). Now by Hopf’s boundary point lemma, we have

$$\begin{aligned} \frac{\partial \phi (x,t^*)}{\partial {{\textbf{n}}}} >0 \ \text { or } \ \frac{\partial \phi (x,t^*)}{\partial {{\textbf{n}}}} <0 \ \text { respectively.} \end{aligned}$$

This contradicts with the boundary condition (1.2). Hence, (2.8) holds. Then we can extend \(t^*\) to a larger value if \(t^*<T\), which is a contraction. This finishes the proof. \(\square \)

Remark 2.1

The values of \(\beta \) rely on the specific form of the function \(f=-F'\) and may not be unique. In the case F being the double well potential, \(\beta \) can be taken as any value in \([\frac{2\sqrt{3}}{3}, +\infty )\). On the other hand, when F is the Flory-Huggins potential,we can choose \(\beta \in (\rho ,1)\) (cf. [27]), where \(\rho \) is the positive root of \(f(\rho ) =- {F}'(\rho )\).

Remark 2.2

An alternative modification for the ACNS model (1.1) is to adopt the Lagrange multiplier introduced by Brassel and Bretin (cf. [28,29,30,31]), which can be formulated as follows:

$$\begin{aligned} \begin{aligned} L(\phi (t))&=\frac{\int _\Omega f(\phi ({{\textbf{y}}},t))d{{\textbf{y}}}}{\int _\Omega \sqrt{4F(\phi ({{\textbf{y}}},t))}d{{\textbf{y}}}}\sqrt{4F(\phi ({{\textbf{x}}},t))},&\; {{\textbf{x}}}\in \Omega . \end{aligned} \end{aligned}$$
(2.9)

In this case, we modify the Flory-Huggins potential by a constant as \({{\tilde{F}}}(\phi ):=F(\phi )+ C\), where \(0<\theta <\theta _c\) and \(C=C(\theta ,\theta _c)\) is chosen such that \(\min _{-1<\phi <1}{{{\tilde{F}}}(\phi )}=0\). It is easy to see that \(C=-\theta [(1+\rho )\ln (1+\rho )+(1-\rho )\ln (1-\rho )]/2 +\theta _c\rho ^2/2 \), where \(\rho \) is the positive root of \(f(\rho ) =- {{\tilde{F}}}'(\rho )\). Furthermore, we can show that \(\rho \in \left( \sqrt{1-\theta /\theta _c},1\right) \). It follows that \(\min _{-1<\phi <1}{ {{\tilde{F}}}(\phi )}={{\tilde{F}}}(\rho )={{\tilde{F}}}(-\rho )=0\). The same proof technique used in Proposition 2.1 applies equally well here to demonstrate that the solutions to this new model also satisfy the MBP but with a different maximum bound. In this case, we do not rely on the Assumption  1. Indeed, treating \(\int _\Omega f(\phi ({{\textbf{y}}},t))d{{\textbf{y}}}/\int _\Omega \sqrt{4F(\phi ({{\textbf{y}}},t))}d{{\textbf{y}}} \) as a given coefficient, the nonlocal Eq. (1.1a) can be viewd as a semi-linear equation. Now the key is to note the fact that \(F(1)=0\) for the double well potential (2.5) and \({{\tilde{F}}}(\rho )=0\) for the modified Flory-Huggins potential, then we can apply the comparison principle and Hopf’s boundary point lemma to show that the MBP holds with the corresponding bounds 1 and \(\rho \) respectively in this case.

In order to preserve the MBP of the numerical solution, we rewrite the Eq. (1.1) into an equivalent form with a stabilizing constant \(\kappa >0\),

$$\begin{aligned}&\partial _t\phi +{{\textbf{u}}}\cdot \nabla \phi =-{{\mathcal {M}}}\mu ,&\;\text {in}\;\Omega \times (0,T), \end{aligned}$$
(2.10a)
$$\begin{aligned}&\mu =-\lambda \left( \epsilon ^2\Delta -\kappa \right) \phi -\lambda \left( {{\bar{f}}}(\phi )+\kappa \phi \right) ,&\;\text {in}\;\Omega \times (0,T), \end{aligned}$$
(2.10b)
$$\begin{aligned}&{{\textbf{u}}}_t+\gamma ({{\textbf{u}}}\cdot \nabla ){{\textbf{u}}}-\nu \Delta {{\textbf{u}}}+\nabla p=\mu \nabla \phi ,&\;\text {in}\;\Omega \times (0,T), \end{aligned}$$
(2.10c)
$$\begin{aligned}&\nabla \cdot {{\textbf{u}}}=0,&\;\text {in}\; \Omega \times (0,T), \end{aligned}$$
(2.10d)

where \({{\bar{f}}}(\phi )=f(\phi )-L(\phi (t))\) and \(L(\phi (t))\) is defined in (1.3). Moreover, the stabilizing constant \(\kappa \) is assumed to satisfy

$$\begin{aligned} \kappa \ge \left\| {{\bar{f}}}'(\xi )\right\| _{C[-\beta ,\beta ]}. \end{aligned}$$
(2.11)

Lemma 2.1

( [16]) Let \(B\in {{\mathcal {R}}}^{N,N}\) and \(A=aI-B\), where \(a>0\) is a constant. If \(B=(b_{ij})\) is a negative diagonally dominant matrix, i.e., \(b_{ii}<0\), \(b_{ii}+\sum _{j\ne i}|b_{ij}|\le 0,\) for all i, then A is invertible and its inverse satisfies \(\Vert A^{-1}\Vert _{L^\infty (\Omega )}\le \frac{1}{a}.\)

Lemma 2.2

( [18]) Under Assumption 1 and the condition \(\kappa \ge \left\| {{\bar{f}}}'(\xi )\right\| _{C[-\beta ,\beta ]}\), we obtain that \(\left| {{\bar{f}}}(\xi )+\kappa \xi \right| \le \kappa \beta \) for any \(\xi \in [-\beta , \beta ]\).

Recalling Proposition 2.1 and noting the fact that \(F(\phi )\) is bounded from below on \([-\beta , \beta ]\), it holds that

$$\begin{aligned} -C_*\le E_1(\phi (t))=\int _\Omega \lambda F(\phi (t))d{{\textbf{x}}}\le C^*. \end{aligned}$$

for some constants \(C_*, C^*\ge 0\).

If we introduce an SAV \( s(t)=E_1(\phi (t)), \) and recast the governing system (1.1) as the following

$$\begin{aligned}&\partial _t\phi +\xi {{\textbf{u}}}\cdot \nabla \phi =-{{\mathcal {M}}}\mu ,\\&\mu =-\lambda (\epsilon ^2\Delta \phi +\xi {{\bar{f}}}(\phi ))+\kappa \lambda \xi (\phi -\phi ),\\&{{\textbf{u}}}_t+\xi ({{\textbf{u}}}\cdot \nabla ){{\textbf{u}}}-\nu \Delta {{\textbf{u}}}+\nabla p=\mu \nabla \phi ,\\&\nabla \cdot {{\textbf{u}}}=0,\\&s_t=\int _\Omega -\mu \nabla \phi \cdot {{\textbf{u}}}- \xi \left( \lambda {{\bar{f}}}(\phi )\phi _t-\gamma {{\textbf{u}}}\cdot \nabla {{\textbf{u}}}\cdot {{\textbf{u}}} -\nabla \cdot ({{\textbf{u}}}\phi )\mu \right) d{{\textbf{x}}}, \end{aligned}$$

where

$$\begin{aligned} \xi =\frac{\sigma (s)}{\sigma (E_1(\phi , {{\textbf{u}}}))}, \end{aligned}$$
(2.12)

then we have the following energy form which is equivalent to \({{\mathcal {E}}}(\phi )\)

$$\begin{aligned} E(\phi ,{{\textbf{u}}}, s)=\int _\Omega \left( \frac{\lambda \epsilon ^2}{2}|\nabla \phi |^2+\frac{1}{2}|{{\textbf{u}}}|^2\right) d{{\textbf{x}}}+s\ge -C_*. \end{aligned}$$

Here, \(\sigma : \mathbb {R} \rightarrow \mathbb {R}\) is a function that satisfies the following two conditions:

  1. (a)

    \(\sigma >0\) for all \(x\in \mathbb {R} \);

  2. (b)

    \(\sigma \) is continuously differentiable and \( \sigma ' \ge 0 \) for all \(x\in \mathbb {R}\).

These conditions play a crucial role in preserving the MBP of the numerical schemes proposed in this paper.

Remark 2.3

Some nontrivial choices for the function \(\sigma \) can be found in [32].

We now introduce some standard notations. The two-dimensional domain \(\Omega \) is partitioned as \(\Omega _x \times \Omega _y\), where

$$\begin{aligned} \begin{aligned}&\Omega _x: 0=x_0< x_1<\cdots<x_{N_x-1}<x_{N_x}=L_{x}, \\&\Omega _y: 0=y_0<y_1<\cdots<y_{N_y-1}<y_{N_y}=L_{y}. \end{aligned} \end{aligned}$$

Additionally, we use the following notations:

$$\begin{aligned} \left\{ \begin{array}{l} x_{-1 / 2}=x_0=0, \ x_{N_x+1 / 2}=x_{N_x}=L_{x}, \\ y_{-1 / 2}=y_0=0,\ y_{N_y+1 / 2}=y_{N_y}=L_{y}. \end{array}\right. \end{aligned}$$

For possible integers \(i, j, \ 0 \le i \le N_x, \ 0 \le j \le N_y\), we define

$$\begin{aligned} \begin{aligned}&x_{i+1 / 2}=\frac{x_i+x_{i+1}}{2}, \quad h_x=x_{i+1}-x_i=x_{i+1 / 2}-x_{i-1 / 2}, \\&y_{j+1 / 2}=\frac{y_j+y_{j+1}}{2}, \quad h_y=y_{j+1}-y_j=y_{j+1 / 2}-y_{j-1 / 2}, \\&\Omega _{i+1 / 2, j+1 / 2}=\left( x_i, x_{i+1}\right) \times \left( y_j, y_{j+1}\right) . \end{aligned} \end{aligned}$$

For a function f(x, y), let \(f_{l, m}\) denote \(f\left( x_l, y_m\right) \) where l may take values \(i, i+1 / 2\) and m may take values \(j, j+1 / 2\) for integers \(i, j, \ 0 \le i \le N_x, \ 0 \le j \le N_y\). For discrete functions \(f_{l, m}\) with values at proper nodal points, define

$$\begin{aligned} {\left\{ \begin{array}{ll} \left[ d_x f\right] _{i+1 / 2, m}=\frac{f_{i+1, m}-f_{i, m}}{h_x}, & \left[ D_y f\right] _{l, j+1}=\frac{f_{l, j+3 / 2}-f_{l, j+1 / 2}}{h_y}, \\ \left[ D_x f\right] _{i+1, m}=\frac{f_{i+3 / 2, m}-f_{i+1 / 2, m}}{h_x},& \left[ d_y f\right] _{l, j+1 / 2}=\frac{f_{l, j+1}-f_{l, j}}{h_y},\\ \left[ \nabla _x f\right] _{i+1/2, m}=\frac{f_{i+3 / 2, m}-f_{i-1 / 2, m}}{2h_x},& \left[ \nabla _y f\right] _{l, j+1/2}=\frac{f_{l, j+3 / 2}-f_{l, j-1 / 2}}{2h_y}, \end{array}\right. } \end{aligned}$$

and \({{\textbf{D}}}H=(D_xH, D_yH)\) for any discrete scalar or vector function H. We define the discrete \(l^2\) inner products and norms as follows:

$$\begin{aligned}&(f, g)_{l^2, M} \equiv \sum _{i=0}^{N_x-1} \sum _{j=0}^{N_y-1} h_xh_y f_{i+1 / 2, j+1 / 2} g_{i+1 / 2, j+1 / 2}, \quad \Vert f\Vert _{l^2, \xi }^2 \equiv (f, f)_{l^2, \xi }, \\&(f, g)_{l^2, T_x} \equiv \sum _{i=0}^{N_x} \sum _{j=1}^{N_y-1} h_xh_y f_{i, j} g_{i, j}, \quad (f, g)_{l^2, T_y} \equiv \sum _{i=1}^{N_x-1} \sum _{j=0}^{N_y} h_xh_y f_{i, j} g_{i, j}. \end{aligned}$$

We further define discrete \(l^2\) inner products and norms as follows:

$$\begin{aligned} \begin{aligned} (f, g)_{l^2, T, M}&\equiv \sum _{i=1}^{N_x-1} \sum _{j=0}^{N_y-1} h_xh_y f_{i, j+1 / 2} g_{i, j+1 / 2}, \quad \Vert f\Vert _{l^2, T, M}^2\hspace{-0.2cm}&\equiv (f, f)_{l^2, T, M},\\ (f, g)_{l^2, M, T}&\equiv \sum _{i=0}^{N_x-1} \sum _{j=1}^{N_y-1} h_xh_y f_{i+1 / 2, j} g_{i+1 / 2, j}, \quad \Vert f\Vert _{l^2, M, T}^2\hspace{-0.2cm}&\equiv (f, f)_{l^2, M, T}. \end{aligned} \end{aligned}$$

For vector-valued functions \({{\textbf{u}}}=\left( u_1, u_2\right) \), we define

$$\begin{aligned} \begin{aligned} \left\| d_x u_1\right\| _{l^2, M}^2 \hspace{-0.15cm}\equiv \hspace{-0.2cm} \sum _{i=0}^{N_x-1} \sum _{j=0}^{N_y-1} h_xh_y\left| d_x u_{1, i+1 / 2, j+1 / 2}\right| ^2\hspace{-0.2cm}, \ \ \left\| D_y u_1\right\| _{l^2, T_y}^2 \hspace{-0.15cm}\equiv \hspace{-0.2cm}\sum _{i=1}^{N_x-1} \sum _{j=0}^{N_y}h_xh_y\left| D_y u_{1, i, j}\right| ^2\hspace{-0.2cm}, \end{aligned} \end{aligned}$$

and \(\left\| d_y u_2\right\| _{l^2, M},\left\| D_x u_2\right\| _{l^2, T_x}\) can be defined similarly. Finally, we define the discrete \(H^1\)-norm and the discrete \(l^2\)-norm of a vectored-valued function \({{\textbf{u}}}\),

$$\begin{aligned} \begin{aligned} \Vert D {{\textbf{u}}}\Vert ^2&\equiv \left\| d_x u_1\right\| _{l^2, M}^2+\left\| D_y u_1\right\| _{l^2, T_y}^2+\left\| D_x u_2\right\| _{l^2, T_x}^2+\left\| d_y u_2\right\| _{l^2, M}^2. \\ \Vert {{\textbf{u}}}\Vert _{l^2}^2&\equiv \left\| u_1\right\| _{l^2, T, M}^2+\left\| u_2\right\| _{l^2, M, T}^2. \end{aligned} \end{aligned}$$

Denote \(\left\{ \Phi ^n, W^n, S^n, {{\textbf{U}}}^n, P^n \right\} _{n=1}^N\) to be the approximations to \(\left\{ \phi ^n, \mu ^n, s^n, {{\textbf{u}}}^n, p^n \right\} _{n=1}^N\), respectively, with the boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} { \left[ D_x \Phi \right] _{0, j+1 / 2}^n=\left[ D_x \Phi \right] _{N_x, j+1 / 2}^n=0,} & 0 \le j \le N_y-1, \\ {\left[ D_y \Phi \right] _{i+1 / 2,0}^n=\left[ D_y \Phi \right] _{i+1 / 2, N_y}^n=0,} & 0 \le i \le N_x-1, \\ {{\tilde{U}}}_{1,0, j+1 / 2}^n={{\tilde{U}}}_{1, N_x, j+1 / 2}^n=0,& 0 \le j \le N_y-1, \\ {{\tilde{U}}}_{1, i, 0}^n={{\tilde{U}}}_{1, i, N_y}^n=0, & 0 \le i \le N_x, \\ {{\tilde{U}}}_{2,0, j}^n={{\tilde{U}}}_{2, N_x, j}^n=0, & 0 \le j \le N_y, \\ {{\tilde{U}}}_{2, i+1 / 2,0}^n={{\tilde{U}}}_{2, i+1 / 2, N_y}^n=0, & 0 \le i \le N_x-1, \end{array}\right. } \end{aligned}$$

and initial conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} \Phi _{i+1 / 2, j+1 / 2}^0=\phi _{i+1 / 2, j+1 / 2}^0, & 0 \le i \le N_x-1, \quad 0 \le j \le N_y-1, \\ {{\tilde{U}}}_{1, i, j+1 / 2}^0=u_{1, i, j+1 / 2}^0, & 0 \le i \le N_x, \quad 0 \le j \le N_y, \\ {{\tilde{U}}}_{2, i+1 / 2, j}^0=u_{2, i+1 / 2, j}^0, & 0 \le i \le N_x, \quad 0 \le j \le N_y, \end{array}\right. } \end{aligned}$$

where \(\phi ^0, {{\textbf{u}}}^0\) are given initial conditions.

3 Fully Discrete Generalized sESAV-MBP-Preserving Schemes

In this section, we construct first- and second-order (in time) linear numerical schemes for the nonlocal ACNS model that preserves the energy dissipation law unconditionally and the MBP. For simplicity, we only consider the case that \(h=h_x =h_y\), i.e., equal uniform grids are used both in the x and y-directions.

3.1 Semi-Discretized Pressure-Correction Generalized sESAV Scheme

The first-order semi-discretized pressure-correction [8] generalized sESAV scheme is as follows:

Step 1: given \((\phi ^n, {{\textbf{u}}}^n)\), compute \((\phi ^{n+1}, \mu ^{n+1})\) such that

$$\begin{aligned}&\frac{\phi ^{n+1}-\phi ^{n}}{\Delta t}+\xi ^n{{\textbf{u}}}^n\cdot \nabla \phi ^{n+1}=-{{\mathcal {M}}}\mu ^{n+1}; \end{aligned}$$
(3.13a)
$$\begin{aligned}&\mu ^{n+1}=-\lambda (\epsilon ^2\Delta \phi ^{n+1}+\xi ^n{{\bar{f}}}(\phi ^n))+\kappa \lambda \xi ^n(\phi ^{n+1}-\phi ^n); \end{aligned}$$
(3.13b)

Step 2: compute \({\varvec{\tilde{u}}}^{n+1}\) from

$$\begin{aligned} \begin{aligned} \frac{{\varvec{\tilde{u}}}^{n+1}-{{\textbf{u}}}^{n}}{\Delta t} +\xi ^n ({{\textbf{u}}}^{n}\cdot \nabla ){{\textbf{u}}}^{n}-\nu \Delta {\varvec{\tilde{u}}}^{n+1} +\nabla p^n=\mu ^{n+1} \nabla \phi ^{n+1}, \quad {\varvec{\tilde{u}}}^{n+1}|_{\partial \Omega }=0; \end{aligned} \end{aligned}$$
(3.13c)

Step 3: update \({{\textbf{u}}}^{n+1}\) using

$$\begin{aligned} \begin{aligned} \frac{{{\textbf{u}}}^{n+1}-{\varvec{\tilde{u}}}^{n+1}}{\Delta t}+\nabla (p^{n+1}-p^n)=0;~ \nabla \cdot {{\textbf{u}}}^{n+1}=0,~ {{\textbf{u}}}^{n+1} \cdot {{\textbf{n}}} |_{\partial \Omega }=0; \end{aligned} \end{aligned}$$
(3.13d)

Step 4: solve \(s^{n+1}\) from

$$\begin{aligned}&\frac{{{\tilde{s}}}^{n+1}-s^{n}}{\Delta t}=\int _\Omega -\mu ^{n+1} \nabla \phi ^{n+1}\cdot {\varvec{\tilde{u}}}^{n+1} \nonumber \\&\qquad -\xi ^n \left( \lambda {{\bar{f}}}(\phi ^n)\frac{\phi ^{n+1}-\phi ^{n}}{\Delta t} -\gamma {{\textbf{u}}}^n\cdot \nabla {{\textbf{u}}}^n\cdot {\varvec{\tilde{u}}}^{n+1} -\nabla \cdot ({{\textbf{u}}}^{n}\phi ^{n+1})\mu ^{n+1} \right) d{{\textbf{x}}};\nonumber \\&s^{n+1}=\max \left\{ {{\tilde{s}}}^{n+1},-C_*-E_{el}[\phi ^{n+1},{{\textbf{u}}}^{n+1},p^{n+1}]\right\} , \end{aligned}$$
(3.13e)

where

$$\begin{aligned} \xi ^n=\frac{\sigma (s^n)}{\sigma (E_1(\phi ^n))}, \end{aligned}$$

and

$$\begin{aligned} E_{el}[\phi ^{n+1},{{\textbf{u}}}^{n+1},p^{n+1}]=\frac{\lambda \epsilon ^2}{2}\Vert \nabla \phi ^{n+1} \Vert ^2 +\frac{1}{2}\Vert {{\textbf{u}}}^{n+1}\Vert ^2 +\frac{\Delta t^2}{2}\Vert \nabla p^{n+1} \Vert ^2. \end{aligned}$$

The second-order semi-discretized pressure-correction generalized sESAV scheme is as follows:

Step 1: given \((\phi ^n, \phi ^{n-1}, {{\textbf{u}}}^n, {{\textbf{u}}}^{n-1})\), compute \((\phi ^{n+1}, \mu ^{n+1})\) such that

$$\begin{aligned} & \begin{aligned} \frac{\phi ^{n+1}-\phi ^{n}}{\Delta t}+\xi ^{\star ,n+1/2}{{\textbf{u}}}^{\star ,n+1/2}\cdot \nabla \phi ^{n+1/2}=-{{\mathcal {M}}}\mu ^{n+1/2}, \end{aligned} \end{aligned}$$
(3.14a)
$$\begin{aligned} & \begin{aligned} \mu ^{n+1/2}=&-\lambda \epsilon ^2\Delta \phi ^{n+1/2}-\lambda \xi ^{\star ,n+1/2}{{\bar{f}}}(\phi ^{\star ,n+1/2})\\&+\kappa \lambda \xi ^{\star ,n+1/2}(\phi ^{n+1/2}-\phi ^{\star ,n+1/2}); \end{aligned} \end{aligned}$$
(3.14b)

Step 2: solve \({\varvec{\tilde{u}}}^{n+1}\) from

$$\begin{aligned} \begin{aligned}&\frac{{\varvec{\tilde{u}}}^{n+1}-{{\textbf{u}}}^{n}}{\Delta t} +\xi ^{\star ,n+1/2} ({{\textbf{u}}}^{\star ,n+1/2}\cdot \nabla ){{\textbf{u}}}^{\star ,n+1/2}-\nu \Delta \frac{{\varvec{\tilde{u}}}^{n+1}+{{\textbf{u}}}^n}{2}\\&\qquad +\nabla p^n=\mu ^{n+1/2} \nabla \phi ^{n+1/2}, \quad {\varvec{\tilde{u}}}^{n+1}|_{\partial \Omega }=0; \end{aligned} \end{aligned}$$
(3.14c)

Step 3: update \({{\textbf{u}}}^{n+1}\) using

$$\begin{aligned} \begin{aligned}&\frac{{{\textbf{u}}}^{n+1}-{\varvec{\tilde{u}}}^{n+1}}{\Delta t}+\frac{1}{2}\nabla (p^{n+1}-p^n)=0,\\&\nabla \cdot {{\textbf{u}}}^{n+1}=0, \quad {{\textbf{u}}}^{n+1}\cdot {{\textbf{n}}} |_{\partial \Omega }=0; \end{aligned} \end{aligned}$$
(3.14d)

Step 4: solve \(s^{n+1}\) from

$$\begin{aligned}&\frac{{{\tilde{s}}}^{n+1}-s^{n}}{\Delta t}=\int _\Omega -\mu ^{n+1/2} \nabla \phi ^{n+1/2}\cdot \frac{{\varvec{\tilde{u}}}^{n+1}+{{\textbf{u}}}^n}{2} -\lambda \xi ^{\star ,n+1/2} {{\bar{f}}}(\phi ^{\star ,n+1/2})\frac{\phi ^{n+1}-\phi ^{n}}{\Delta t}\nonumber \\&\quad \quad +\xi ^{\star ,n+1/2} \left( \gamma {{\textbf{u}}}^{\star ,n+1/2}\cdot \nabla {{\textbf{u}}}^{\star ,n+1/2}\cdot \frac{{\varvec{\tilde{u}}}^{n+1}+{{\textbf{u}}}^n}{2} +\nabla \cdot ({{\textbf{u}}}^{\star ,n+1/2}\phi ^{n+1/2})\mu ^{n+1/2} \right) \nonumber \\&\quad \quad +\kappa \xi ^{\star ,n+1/2}(\phi ^{n+1/2}-\phi ^{\star ,n+1/2})\cdot \frac{\phi ^{n+1}-\phi ^{n}}{\Delta t}d{{\textbf{x}}},\nonumber \\&s^{n+1}=\max \left\{ {{\tilde{s}}}^{n+1},-C_*-E_{el}[\phi ^{n+1},{{\textbf{u}}}^{n+1},p^{n+1}]\right\} , \end{aligned}$$
(3.14e)

where

$$\begin{aligned} \xi ^{\star ,n+1/2}=\frac{\sigma (s^{\star ,n+1/2})}{\sigma (E_1(\phi ^{\star ,n+1/2}))}, \end{aligned}$$

and

$$\begin{aligned} E_{el}[\phi ^{n+1},{{\textbf{u}}}^{n+1},p^{n+1}]=\frac{\lambda \epsilon ^2}{2}\Vert \nabla \phi ^{n+1} \Vert ^2 +\frac{1}{2}\Vert {{\textbf{u}}}^{n+1}\Vert ^2 +\frac{\Delta t^2}{8}\Vert \nabla p^{n+1} \Vert ^2. \end{aligned}$$

\((\cdot )^{n+1/2}=\frac{1}{2}(\cdot )^{n+1}+\frac{1}{2}(\cdot )^{n}\) and \((\cdot )^{\star ,n+1/2}\) are generated by the first-order scheme (3.13) with the time step size \(\Delta t/2\).

3.2 Fully Discrete MBP-sESAV Scheme with First-Order in Time

Scheme 1

(MBP-sESAV1 scheme) Based on the MAC discretization, the fully discrete first-order pressure-correction generalized sESAV scheme is given as follows:

Step 1: given \((\Phi ^n, {{\textbf{U}}}^n)\), compute \((\Phi ^{n+1}, W^{n+1})\) such that

$$\begin{aligned}&\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t}+\chi ^n\left( \Pi _h\left( U_1^{n}\right) \nabla _x +\Pi _h\left( U_2^{n}\right) \nabla _y\right) \Phi ^{n+1} =-{{\mathcal {M}}}W^{n+1}, \end{aligned}$$
(3.15a)
$$\begin{aligned}&W^{n+1}=-\lambda \epsilon ^2\left[ d_x D_x \Phi +d_y D_y \Phi \right] ^{n+1} -\lambda \chi ^n {{\bar{f}}}(\Phi ^{n}) \nonumber \\&\quad +\kappa \lambda \chi ^n\left( \Phi ^{n+1}-\Phi ^n\right) ; \end{aligned}$$
(3.15b)

Step 2: solve \({\varvec{\tilde{U}}}^{n+1}\) from

$$\begin{aligned}&\frac{{{\tilde{U}}}_1^{n+1}-U_1^{n}}{\Delta t}+\chi ^nC_1^{n}-\nu D_x\left( d_x {{\tilde{U}}}_1\right) ^{n+1}-\nu d_y\left( D_y {{\tilde{U}}}_1\right) ^{n+1 } \nonumber \\&\quad +\left[ D_x P\right] ^{n}=\Pi _h W^{n+1}\left[ D_x \Phi \right] ^{n+1},\ {{{\tilde{U}}}_1^{n+1}|_{\partial \Omega }=0}, \end{aligned}$$
(3.15c)
$$\begin{aligned}&\frac{{{\tilde{U}}}_2^{n+1}-U_1^{n}}{\Delta t}+\chi ^nC_2^{n} -\nu D_y\left( d_y {{\tilde{U}}}_2\right) ^{n+1} -\nu d_x\left( D_x {{\tilde{U}}}_2\right) ^{n+1}, \nonumber \\&\quad +\left[ D_y P\right] ^{n}=\Pi _h W^{n+1}\left[ D_y \Phi \right] ^{n+1},\ {{{\tilde{U}}}_2^{n+1}|_{\partial \Omega }=0}; \end{aligned}$$
(3.15d)

Step 3: given \(({\varvec{\tilde{U}}}^{n+1}, P^n)\), find \({(}{{\textbf{U}}}^{n+1}{,P^{n+1})}\) by solving

$$\begin{aligned}&\frac{U_1^{n+1}-{{\tilde{U}}}_1^{n+1}}{\Delta t}+([D_xP]^{n+1}-[D_xP]^n)=0,\end{aligned}$$
(3.15e)
$$\begin{aligned}&\frac{U_2^{n+1}-{{\tilde{U}}}_2^{n+1}}{\Delta t}+([D_yP]^{n+1}-[D_yP]^n)=0,\end{aligned}$$
(3.15f)
$$\begin{aligned}&\left[ d_xU_1\right] ^{n+1}+\left[ d_y U_2\right] ^{n+1}=0, \quad {{\textbf{U}}}^{n+1}\cdot {{\textbf{n}}}|_{\partial \Omega }=0; \end{aligned}$$
(3.15g)

By taking the operator dx of (3.15e) and the operator dy of (3.15f), we find that (3.15g) is equivalent to

$$\begin{aligned}&(d_x D_x +d_y D_y)(P^{n+1}-P^n)=\frac{1}{\Delta t}(d_x {{\tilde{U}}}_1^{n+1}+d_y {{\tilde{U}}}_2^{n+1}),\ {{\textbf{D}}} (P^{n+1}-P^n) \cdot {{\textbf{n}}}|_{\partial \Omega }=0,\end{aligned}$$
(3.15h)
$$\begin{aligned}&U_1^{n+1}={{\tilde{U}}}_1^{n+1}-\Delta t([D_xP]^{n+1}-[D_xP]^n),\end{aligned}$$
(3.15i)
$$\begin{aligned}&U_2^{n+1}={{\tilde{U}}}_2^{n+1}-\Delta t([D_yP]^{n+1}-[D_yP]^n); \end{aligned}$$
(3.15j)

Step 4: solve \(S^{n+1}\) from

$$\begin{aligned} \begin{aligned}&\frac{{{\tilde{S}}}^{n+1}-S^{n}}{\Delta t}= -\left( \Pi _h W^{n+1}D_x \Phi ^{n+1},{{\tilde{U}}}_1^{n+1}\right) _{l^2,T, M} -\left( \Pi _h W^{n+1}D_y \Phi ^{n+1}, {{\tilde{U}}}_2^{n+1}\right) _{l^2, M, T}\\&\quad -\lambda \chi ^n\left( {{\bar{f}}}\left( \Phi ^{n}\right) , \frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t}\right) _{l^2, M} +\gamma \chi ^n\left( C_1^n, {{\tilde{U}}}_1^{n+1} \right) _{l^2, T, M}\\&\quad +\gamma \chi ^n\left( C_2^n, {{\tilde{U}}}_2^{n+1} \right) _{l^2, M, T} +\chi ^n\left( \Pi _h\left( U_1^{n}\right) {{\bar{d}}}_x \Phi ^{n+1} +\Pi _h\left( U_2^{n}\right) {{\bar{d}}}_y \Phi ^{n+1}, W^{n+1}\right) _{l^2, M},\\&S^{n+1}=\max \left\{ {{\tilde{S}}}^{n+1},-C_*-E^{n+1}_{el}[\Phi ,{{\textbf{U}}},P]\right\} , \end{aligned} \end{aligned}$$
(3.15k)

where \(\Pi _h\) is the bilinear interpolation operator and

$$\begin{aligned} \chi ^n&=\frac{\sigma (S^n)}{\sigma (E_1^h\left( \Phi ^{n}\right) )},\\ C_1^n&=[U_1 D_x\left( \Pi _h U_1\right) +\Pi _hU_2 d_y\left( \Pi _hU_1\right) ]^n,\\ C_2^n&=[\Pi _hU_1 d_x\left( \Pi _hU_2\right) +U_2 D_y\left( \Pi _h U_2\right) ]^n,\\ E^{n+1}_{el}[\Phi ,{{\textbf{U}}},P]&=\frac{\lambda \epsilon ^2}{2}\Vert {{\textbf{D}}} \Phi ^{n+1} \Vert ^2 +\frac{1}{2}\Vert {{\textbf{U}}}^{n+1}\Vert ^2 +\frac{\Delta t^2}{2}\Vert {{\textbf{D}}} P^{n+1} \Vert ^2. \end{aligned}$$

Remark 3.1

We only need to calculate two linear elliptic equations in Step 2, and two Poisson-type equations in Step 3, which leads to extremely efficient calculations. Finally, we can determine \(S^{n+1}\) by solving a linear algebraic equation with negligible computational cost.

Lemma 3.1

([33]) Let \(\{ V_{1,i,j+1/2}\}, \{ V_{2,i+1/2,j} \}\), \(\{ q_{1,i+1/2,j+1/2} \}\), \(\{q_{2,i+1/2,j+1/2}\}\) be discrete functions with \(V_{1,0,j+1/2} = V_{1,Nx,j+1/2} = V_{2,i+1/2,0}=V_{2,i+1/2,Ny}= 0\) for proper integers i and j. Then, there holds

$$\begin{aligned} (D_xq_1, V_1)_{l^2,T,M} = -(q_1, d_xV_1)_{l^2,M},\quad (D_yq_2, V_2)_{l^2,M,T} = -(q_2, d_yV_2)_{l^2,M}. \end{aligned}$$

We proceed to prove the unconditional energy dissipation and MBP of the scheme defined in (3.13) as follows.

Theorem 3.1

(Energy stable of the MBP-sESAV1 scheme) The scheme (1) is energy stable in the sense that

$$\begin{aligned} E_h^{n+1}(\Phi , U, S)- E_h^{n}(\Phi , U, S)\le -M\Delta t\Vert W^{n+1}\Vert ^2_{l^2,M} -\nu \Delta t\Vert D {\varvec{\tilde{U}}}^{n+1}\Vert ^2, \end{aligned}$$
(3.16)

where

$$\begin{aligned} E_h^{n+1}(\Phi , U, S)=\frac{\lambda \epsilon ^2}{2}\Vert {{\textbf{D}}} \Phi ^{n+1} \Vert ^2_{l^2} +\frac{1}{2}\Vert {{\textbf{U}}}^{n+1}\Vert ^2_{l^2} +\frac{\Delta t^2}{2}\Vert {{\textbf{D}}}P^{n+1} \Vert ^2_{l^2} +S^{n+1}. \end{aligned}$$

Proof

Multiplying (3.15a) with \(W^{n+1} _{i+1/2,j+1/2}h_xh_y\) and taking summation over i, j for \(0\le i \le N_x-1,\ 0 \le j \le N_y-1\), we have

$$\begin{aligned}&( \frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t},W^{n+1})_{l^2, M} +\chi ^n\left( \left( \Pi _h\left( U_1^{n}\right) \nabla _x +\Pi _h\left( U_2^{n}\right) \nabla _y\right) \Phi ^{n+1},W^{n+1}\right) _{l^2, M}\nonumber \\&\quad = -{{\mathcal {M}}}\Vert W^{n+1}\Vert _{l^2,M}^2. \end{aligned}$$
(3.17)

Multiplying (3.15b) with \(\frac{(\Phi ^{n+1} -\Phi ^{n}) _{i+1/2,j+1/2}}{\Delta t}h_xh_y\) and taking summation over i, j for \(0\le i \le N_x-1,\ 0 \le j \le N_y-1\), we have

$$\begin{aligned} (\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t}, W^{n+1})_{l^2, M}&=-\lambda \epsilon ^2(d_x D_x \Phi ^{n+1}+d_y D_y \Phi ^{n+1},\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t})_{l^2, M}\nonumber \\&\quad -\lambda \chi ^n \left( {{\bar{f}}}(\Phi ^{n}),\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t}\right) _{l^2, M} +\frac{\kappa \lambda \chi ^n}{\Delta t}\Vert \Phi ^{n+1}-\Phi ^{n}\Vert ^2_{l^2,M}.\nonumber \\ \end{aligned}$$
(3.18)

Using Lemma 3.1, the first term on the right-hand side of (3.18) can be estimated by

$$\begin{aligned} \begin{aligned}&-(d_x D_x \Phi ^{n+1}+d_y D_y \Phi ^{n+1},\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t})_{l^2, M}\\&\quad =( D_x \Phi ^{n+1},\frac{D_x \Phi ^{n+1}-D_x \Phi ^{n}}{\Delta t})_{l^2, T, M} \\&+(D_y \Phi ^{n+1},\frac{D_y \Phi ^{n+1}-D_y \Phi ^{n}}{\Delta t})_{l^2, M,T}\ge \frac{\Vert {{\textbf{D}}} \Phi ^{n+1} \Vert _{l^2}^2-\Vert {{\textbf{D}}} \Phi ^{n} \Vert _{l^2}^2}{2\Delta t}. \end{aligned} \end{aligned}$$
(3.19)

Multiplying (3.15c) by \({{\tilde{U}}}^{n+1}_{1,i,j+1/2}h_xh_y\), and taking summation over i, j for \(1 \le i \le N_x-1\), \(0 \le j \le N_y-1\) yields

$$\begin{aligned} \begin{aligned}&( \frac{{{\tilde{U}}}_1^{n+1}-U_1^{n}}{\Delta t}, {{\tilde{U}}}_1^{n+1})_{l^2, T, M}+\chi ^n(C_1^{n},{{\tilde{U}}}_1^{n+1})_{l^2, T, M}\\&\quad +\nu \Vert d_x {{\tilde{U}}}_1^{n+1}\Vert _{l^2, M} +\nu \Vert D_y {{\tilde{U}}}_1^{n+1}\Vert _{l^2, T_y}\\&\quad -(P^{n},d_x {{\tilde{U}}}_1^{n+1})_{l^2, M} -(\Pi _hW^{n+1}D_x \Phi ^{n+1},{{\tilde{U}}}_1^{n+1})_{l^2, T, M}=0. \end{aligned} \end{aligned}$$
(3.20)

Multiplying (3.15d) by \({{\tilde{U}}}^{n+1}_{2,i+1/2,j}h_xh_y\), and taking summation over i, j for \(0 \le i \le N_x-1\), \(1 \le j \le N_y-1\) leads to

$$\begin{aligned} \begin{aligned}&(\frac{{{\tilde{U}}}_2^{n+1}-U_2^{n}}{\Delta t}, {{\tilde{U}}}_2^{n+1})_{l^2, M, T}+\chi ^n(C_2^{n},{{\tilde{U}}}_2^{n+1})_{l^2, M, T}\\&\quad +\nu \Vert d_x {{\tilde{U}}}_2^{n+1}\Vert _{l^2, M} +\nu \Vert D_x {{\tilde{U}}}_2^{n+1}\Vert _{l^2, T_x}\\&\quad -(P^{n},d_y {{\tilde{U}}}_2^{n+1})_{l^2, M} -(\Pi _h W^{n+1}D_y \Phi ^{n+1},{{\tilde{U}}}_2^{n+1})_{l^2, M, T}=0. \end{aligned} \end{aligned}$$
(3.21)

Next, we rewrite (3.15e)-(3.15f) as

$$\begin{aligned} \frac{U_1^{n+1}}{\sqrt{\Delta t}}+\sqrt{\Delta t}D_xP^{n+1} =\frac{{{\tilde{U}}}_1^{n+1}}{\sqrt{\Delta t}}+\sqrt{\Delta t}D_xP^{n},\\ \frac{U_2^{n+1}}{\sqrt{\Delta t}}+\sqrt{\Delta t}D_yP^{n+1}=\frac{{{\tilde{U}}}_2^{n+1}}{\sqrt{\Delta t}}+\sqrt{\Delta t}D_yP^{n}, \end{aligned}$$

now taking the discrete inner product with themselves on both sides and summing them up, it is clear that we have

$$\begin{aligned} \begin{aligned} \frac{1}{\Delta t}\Vert {{\textbf{U}}}^{n+1}\Vert ^2_{l^2} +\Delta t\Vert {{\textbf{D}}} P^{n+1}\Vert ^2_{l^2} = \frac{1}{\Delta t}\Vert {\varvec{\tilde{U}}}^{n+1}\Vert ^2_{l^2} +\Delta t\Vert {{\textbf{D}}} P^{n}\Vert ^2_{l^2} \\ -2(P^{n},d_x {{\tilde{U}}}_1^{n+1})_{l^2, M} -2(P^{n},d_y {{\tilde{U}}}_2^{n+1})_{l^2, M}. \end{aligned} \end{aligned}$$
(3.22)

Combining (3.17)-(3.21) with (3.22), (3.15k) and (3.15g), we obtain

$$\begin{aligned} E_h^{n+1}(\Phi , U, {{\tilde{S}}})- E_h^{n}(\Phi , U, S)\le 0. \end{aligned}$$

If \({{\tilde{s}}}^{n+1}\ge -C_*-E^{n+1}_{el}[\Phi ,{{\textbf{U}}},P]\), it follows that \(S^{n+1}={{\tilde{S}}}^{n+1}\), and, consequently,

$$\begin{aligned} E_h^{n+1}(\Phi , U, S)- E_h^{n}(\Phi , U, S)\le 0. \end{aligned}$$
(3.23)

In the case where \({{\tilde{S}}}^{n+1} < -C_*-E^{n+1}_{el}[\Phi ,{{\textbf{U}}},P]\), we observe that

$$\begin{aligned} S^{n+1}+E^{n+1}_{el}[\Phi ,{{\textbf{U}}},P]=-C_*\le S^{n}+E^{n}_{el}[\Phi ,{{\textbf{U}}},P], \end{aligned}$$

leading directly to (3.16). \(\square \)

Corollary 3.1

It holds \(S^{n}\le {{\mathcal {E}}}_h[\Phi _{\text {init}},{{\textbf{U}}}_{\text {init}}]\) for any \(\kappa \ge 0\).

Proof

By Theorem 3.1, and since \(S_0 = E_{1\,h}(\Phi _{\text {init}})\), we have

$$\begin{aligned} \begin{aligned}&\int _{\Omega } \frac{\lambda \epsilon ^2}{2}|{{\textbf{D}}} \Phi ^{n} |^2 +\frac{1}{2}|{{\textbf{U}}}^{n}|^2+\frac{\Delta t^2}{2}|{{\textbf{D}}}P^{n} |^2 d{{\textbf{x}}}+S^{n} \\&\quad =E^{n}_h[\Phi ,{{\textbf{U}}},S] \le E^{n-1}_h[\Phi ,{{\textbf{U}}},S] \le \cdot \cdot \cdot \le E^0_h[\Phi ,{{\textbf{U}}},S] ={{\mathcal {E}}}_h[\Phi _{\text {init}}, {{\textbf{U}}}_{\text {init}}], \end{aligned} \end{aligned}$$
(3.24)

dropping off the nonnegative term, we can easily obtain the desired result. \(\square \)

Remark 3.2

Employing a similar error analysis as in [34], one can conclude that:

$$\begin{aligned} \Vert {{\textbf{u}}}(t^n)-{{\textbf{U}}}^n\Vert _{L^2}\le {{\bar{C}}}(h^2+\Delta t). \end{aligned}$$

Noting the inverse inequality, we derive

$$\begin{aligned} \begin{aligned} \Vert {{\textbf{U}}}^n&\Vert _{L^\infty }\le \Vert {{\textbf{U}}}^n-\Pi _h {{\textbf{u}}}\Vert _{L^\infty }+ \Vert \Pi _h {{\textbf{u}}}-{{\textbf{u}}}(t^n)\Vert _{L^\infty }+ \Vert {{\textbf{u}}}(t^n)\Vert _{L^\infty }\\ \le&{{\bar{C}}}h^{-\frac{d}{2}}\left( \Vert {{\textbf{U}}}^n- {{\textbf{u}}}(t^n)\Vert _{L^2}+ \Vert \Pi _h {{\textbf{u}}}-{{\textbf{u}}}(t^n)\Vert _{L^2} \right) + \Vert \Pi _h {{\textbf{u}}}-{{\textbf{u}}}(t^n)\Vert _{L^\infty }+ \Vert {{\textbf{u}}}(t^n)\Vert _{L^\infty }\\ \le&{{\bar{C}}}h^{-\frac{d}{2}}(h^2+\Delta t)+ \Vert \Pi _h {{\textbf{u}}}-{{\textbf{u}}}(t^n)\Vert _{L^\infty }+ \Vert {{\textbf{u}}}(t^n)\Vert _{L^\infty } \le {{\hat{C}}}, \end{aligned} \end{aligned}$$

with the following estimation \( \Vert \Pi _h{{\textbf{u}}}-{{\textbf{u}}}\Vert _{L^\infty }\le {{\bar{C}}}h^2.\)

Theorem 3.2

(Discrete MBP of the MBP-sESAV1 scheme) Let f be continuously differentiable on \([-\beta , \beta ]\) such that \(\kappa \ge \Vert f'\Vert _{C[ - \beta ,\beta ]}\). Moreover, if h satisfy

$$\begin{aligned} h \le \frac{2\lambda \epsilon ^2{{\mathcal {M}}}}{{{\hat{C}}}G^*}, \end{aligned}$$

where \({{\hat{C}}}>0\) is defined in Remark 3.2 and \(G^*=\exp \left\{ {{\mathcal {E}}}_h\left( \Phi _{\text{ init }}, {{\textbf{U}}}_{\text{ init }}\right) +C_*\right\} \), then the scheme preserves the MBP unconditionally, i.e.,

$$\begin{aligned} \Vert \Phi _{\text {init}}\Vert _{L^{\infty }(\Omega )}\le \beta \quad \Rightarrow \quad \Vert \Phi ^n\Vert _{L^{\infty }(\Omega )}\le \beta ,~ \forall n. \end{aligned}$$

Proof

We prove the statement by induction. Suppose \((\Phi ^n, S^n)\) is given and \(\left\| \Phi ^n\right\| _{L^{\infty }(\Omega )}\le \beta \) for some n. Notice that \(\chi ^n\left( \Phi , S\right) >0\) from its definition. It is obvious that using Corollary 3.1, we can get \(\chi ^n\left( \Phi , S\right) \le \exp \left\{ {{\mathcal {E}}}_h\left( \Phi _{\text{ init }}, {{\textbf{U}}}_{\text{ init }}\right) +C_*\right\} =G^*\left( \Phi _{\text {init}}, {{\textbf{U}}}_{\text {init}}, C_*\right) \).

We eliminate \(\Phi ^{n+1}\) from (3.15a)-(3.15b) to get

$$\begin{aligned} \begin{aligned} \left( (\frac{1}{\Delta t}+{{\mathcal {M}}}\lambda \kappa \chi ^n)I -{{\mathcal {L}}}_{{{\textbf{U}}}^n}\right) \Phi ^{n+1} =\frac{1}{\Delta t}\Phi ^{n}+{{\mathcal {M}}}\lambda \chi ^n\left( {{\bar{f}}}(\Phi ^{n})+\kappa \Phi ^{ n}\right) , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {{\mathcal {L}}}_{{{\textbf{U}}}^n}={{\mathcal {M}}}\lambda \epsilon ^2(d_x D_x +d_y D_y ) -\chi ^n\left( \Pi _h\left( U_1^{n}\right) \nabla _x +\Pi _h\left( U_2^{n}\right) \nabla _y \right) . \end{aligned}$$

Without loss of generality, we shall describe the specific discrete scheme of \({{\mathcal {L}}}_{{{\textbf{U}}}^n}\) for one-dimensional systems, the extensions to two-dimensional and three-dimensional rectangular domains are straightforward.

$$\begin{aligned} {{\mathcal {L}}}_{{{\textbf{U}}}^n}= \left[ \begin{array}{cccc} -w+\frac{\chi ^n\left| \Pi _hU_{1/2}\right| }{2h}& w-\frac{\chi ^n\left| \Pi _hU_{1/2}\right| }{2h}& & \\ w+\frac{\chi ^n\left| \Pi _hU_{3/2}\right| }{2h} & -2w& w-\frac{\chi ^n\left| \Pi _hU_{3/2}\right| }{2h}& \\ & \ddots & \ddots & \ddots \\ & w+\frac{\chi ^n\left| \Pi _hU_{N-3/2}\right| }{2h}& -2w& w-\frac{\chi ^n\left| \Pi _hU_{N-3/2}\right| }{2h}\\ & & w+\frac{\chi ^n\left| \Pi _hU_{N-1/2}\right| }{2h}& -w-\frac{\chi ^n\left| \Pi _hU_{N-1/2}\right| }{2h}, \end{array} \right] \end{aligned}$$

where \(w=\frac{{{\mathcal {M}}}\lambda \epsilon ^2}{h^2}\). Due to \(0<\chi ^n\le G^*\), the condition

$$\begin{aligned} h \max \left\{ \left\| \Pi _hU^n_{1,i,j}\right\| _{L^\infty }, \left\| \Pi _hU^n_{2,i,j}\right\| _{L^\infty } \right\} \le h{{\hat{C}}}\le \frac{2\lambda \epsilon ^2{{\mathcal {M}}}}{G^*}, \end{aligned}$$

can be guaranteed holds, then all off-diagonal entries of \( {{\mathcal {L}}}_{{{\textbf{U}}}^n}\) are non-positive and diagonal entries of \({{\mathcal {L}}}_{{{\textbf{U}}}^n}\) are positive, thus \({{\mathcal {L}}}_{{{\textbf{U}}}^n}\) is a negative diagonally dominant matrix by rows. We can easily demonstrate that the coefficient mareix of (3.15a)-(3.15b) satisfies Lemma 2.1.

Then by Lemma 2.1, we can have

$$\begin{aligned} \left\| \left( \left( \frac{1}{\Delta t}+{{\mathcal {M}}}\kappa \lambda \chi ^n\right) I-{{\mathcal {L}}}_{{{\textbf{U}}}^n} \right) ^{-1}\right\| _{L^{\infty }(\Omega )}\le \left( \frac{1}{\Delta t}+{{\mathcal {M}}}\kappa \lambda \chi ^n\right) ^{-1}. \end{aligned}$$

According to Lemma 2.2, we derive

$$\begin{aligned} \left\| \frac{1}{\Delta t}\Phi ^{n}+{{\mathcal {M}}}\lambda \chi ^n\left( {{\bar{f}}}(\Phi ^{n})+\kappa \Phi ^{ n}\right) \right\| _{L^{\infty }(\Omega )}\le \left( \frac{1}{\Delta t}+{{\mathcal {M}}}\kappa \lambda \chi ^n\right) \beta . \end{aligned}$$

Therefore, we finally obtain

$$\begin{aligned} \left\| \Phi ^{n+1}\right\| _{L^{\infty }(\Omega )}\le \left( \frac{1}{\Delta t}+{{\mathcal {M}}}\kappa \lambda \chi ^n\right) ^{-1} \left( \frac{1}{\Delta t}+{{\mathcal {M}}}\kappa \lambda \chi ^n\right) \beta = \beta . \end{aligned}$$

Since \( \Vert \Phi _{\text {init}}\Vert _{L^{\infty }(\Omega )}\le \beta \), by induction \(\left\| \Phi ^{n}\right\| _{L^{\infty }(\Omega )}\le \beta \) for all n. \(\square \)

3.3 Fully Discrete MBP-sESAV Scheme with Second-Order in Time

Scheme 2

(MBP-sESAV2 scheme) The fully discrete second-order pressure-correction generalized sESAV scheme based on the MAC discretization is as follows:

Step 1: given \((\Phi ^n, \Phi ^{n-1}, {{\textbf{U}}}^n, {{\textbf{U}}}^{n-1})\), compute \((\Phi ^{n+1}, W^{n+1})\) such that

$$\begin{aligned}&\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t} +\chi ^{\star ,n+1/2}\left( \Pi _h \left( U_1^{\star ,n+1/2}\right) \nabla _x +\Pi _h\left( U_2^{\star ,n+1/2}\right) \nabla _y \right) \Phi ^{n+1/2} =-{{\mathcal {M}}}W^{n+1/2} , \end{aligned}$$
(3.25a)
$$\begin{aligned}&W^{n+1/2}=-\lambda \epsilon ^2\left[ d_x D_x \Phi +d_y D_y \Phi \right] ^{n+1/2} -\lambda \chi ^{\star ,n+1/2} {{\bar{f}}}(\Phi ^{\star ,n+1/2}) \nonumber \\&+\kappa \lambda \chi ^{\star ,n+1/2}(\Phi ^{n+1/2}-\Phi ^{\star ,n+1/2}); \end{aligned}$$
(3.25b)

Step 2: solve for \({\varvec{\tilde{U}}}^{n+1}\) from

$$\begin{aligned}&\frac{{{\tilde{U}}}_1^{n+1}-U_1^{n}}{\Delta t} -\nu D_x\left( \frac{d_x{{\tilde{U}}}^{n+1}_1+d_xU^{n}_1}{2}\right) -\nu d_y\left( \frac{D_y {{\tilde{U}}}^{n+1}_1+D_y U^{n}_1}{2}\right) \nonumber \\&\quad +\chi ^{\star ,n+1/2}C_1^{\star ,n+1/2}+\left[ D_x P\right] ^{n}-\Pi _h W^{n+1/2}\left[ D_x \Phi \right] ^{n+1/2}=0,\ {{{\tilde{U}}}_1^{n+1}|_{\partial \Omega }=0}, \end{aligned}$$
(3.25c)
$$\begin{aligned}&\frac{{{\tilde{U}}}_2^{n+1}-U_2^{n}}{\Delta t} -\nu D_y\left( \frac{d_y{{\tilde{U}}}^{n+1}_2+d_yU^{n}_2}{2}\right) -\nu d_x\left( \frac{D_x{{\tilde{U}}}^{n+1}_2+D_xU^{n}_2}{2}\right) \nonumber \\&\quad +\chi ^{\star ,n+1/2}C_2^{\star ,n+1/2}+\left[ D_y P\right] ^{n} -\Pi _hW^{n+1/2}\left[ D_y \Phi \right] ^{n+1/2}=0,\ {{{\tilde{U}}}_2^{n+1}|_{\partial \Omega }=0}; \end{aligned}$$
(3.25d)

Step 3: given \(({\varvec{\tilde{U}}}^{n+1}, P^n)\), find \({(}{{\textbf{U}}}^{n+1}{,P^{n+1})}\) by solving

$$\begin{aligned} \frac{U_1^{n+1}-{{\tilde{U}}}_1^{n+1}}{\Delta t}+\frac{1}{2}(D_xP^{n+1}-D_xP^n)=0, \end{aligned}$$
(3.25e)
$$\begin{aligned} \frac{U_2^{n+1}-{{\tilde{U}}}_2^{n+1}}{\Delta t}+\frac{1}{2}(D_yP^{n+1}-D_yP^n)=0,\end{aligned}$$
(3.25f)
$$\begin{aligned} \left[ d_xU_1\right] ^{n+1}+\left[ d_y U_2\right] ^{n+1}=0, \quad {{\textbf{U}}}^{n+1}\cdot n|_{\partial \Omega }=0; \end{aligned}$$
(3.25g)

Similar procedures for solving (3.25e)-(3.25g) are discussed in (3.15h)-(3.15j) as follows. By taking the operator dx of (3.25e) and the operator dy of (3.25f), we find that (3.25g) is equivalent to

$$\begin{aligned}&(d_x D_x +d_y D_y)(P^{n+1}-P^n)=\frac{2}{\Delta t}(d_x {{\tilde{U}}}_1^{n+1}+d_y {{\tilde{U}}}_2^{n+1}),\ {{\textbf{D}}} (P^{n+1}-P^n) \cdot {{\textbf{n}}}|_{\partial \Omega }=0,\end{aligned}$$
(3.25h)
$$\begin{aligned}&U_1^{n+1}={{\tilde{U}}}_1^{n+1}-\frac{\Delta t}{2}([D_xP]^{n+1}-[D_xP]^n),\end{aligned}$$
(3.25i)
$$\begin{aligned}&U_2^{n+1}={{\tilde{U}}}_2^{n+1}-\frac{\Delta t}{2}([D_yP]^{n+1}-[D_yP]^n); \end{aligned}$$
(3.25j)

Step 4: solve for \(S^{n+1}\) from

$$\begin{aligned}&\frac{{{\tilde{S}}}^{n+1}-S^{n}}{\Delta t}=- \left( \Pi _h W^{n+1/2}D_x \Phi ^{n+1/2},\frac{{{\tilde{U}}}^{n+1}_1+U^{n}_1}{2}\right) _{l^2,T, M}\nonumber \\&-\left( \Pi _h W^{n+1/2}D_y \Phi ^{n+1/2}, \frac{{{\tilde{U}}}^{n+1}_2+U^{n}_2}{2}\right) _{l^2, M, T}\nonumber \\&-\lambda \chi ^{\star ,n+1/2}\left( {{\bar{f}}}\left( \Phi ^{\star ,n+1/2}\right) , \frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t}\right) _{l^2, M}\nonumber \\&+\gamma \chi ^{\star ,n+1/2}\left( C_1^{\star ,n+1/2}, \frac{{{\tilde{U}}}^{n+1}_1+U^{n}_1}{2} \right) _{l^2, T, M} \hspace{-0.5cm}+\gamma \chi ^{\star ,n+1/2}\left( C_2^{\star ,n+1/2},\frac{{{\tilde{U}}}^{n+1}_2+U^{n}_2}{2} \right) _{l^2, M, T}\nonumber \\&+\chi ^{\star ,n+1/2}\left( \left( \Pi _h \left( U_1^{\star ,n+1/2}\right) \nabla _x +\Pi _h\left( U_2^{\star ,n+1/2}\right) \nabla _y \right) \Phi ^{n+1/2}, W^{n+1/2}\right) _{l^2, M}\nonumber \\&+\kappa \chi ^{\star ,n+1/2}\left( \Phi ^{n+1/2}-\Phi ^{\star ,n+1/2},\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t}\right) _{l^2, M},\nonumber \\&S^{n+1}=\max \left\{ {{\tilde{S}}}^{n+1},-C_*-E^{n+1}_{el}[\Phi ,{{\textbf{U}}},P]\right\} , \end{aligned}$$
(3.25k)

where

$$\begin{aligned} \chi ^{\star ,n+1/2}&=\frac{\sigma (S^{\star ,n+1/2})}{\sigma (E_1^h\left( \Phi ^{\star ,n+1/2}\right) )},\\ C_1^{\star ,n+1/2}&=[U_1 D_x\left( \Pi _h U_1\right) +\Pi _hU_2 d_y\left( \Pi _hU_1\right) ]^{\star ,n+1/2},\\ C_2^{\star ,n+1/2}&=[\Pi _hU_1 d_x\left( \Pi _hU_2\right) +U_2 D_y\left( \Pi _h U_2\right) ]^{\star ,n+1/2},\\ E^{n+1}_{el}[\Phi ,{{\textbf{U}}},P]&=\frac{\lambda \epsilon ^2}{2}\Vert {{\textbf{D}}} \Phi ^{n+1} \Vert ^2 +\frac{1}{2}\Vert {{\textbf{U}}}^{n+1}\Vert ^2 +\frac{\Delta t^2}{8}\Vert {{\textbf{D}}} P^{n+1} \Vert ^2. \end{aligned}$$

and for any sequence of \(\{F^{\star ,n+1/2}\}\) is generated by the pressure-correction sESAV1 scheme (1) with the time step size \(\Delta t/2\).

Remark 3.3

The computations of \(({{\textbf{U}}}^{n+1},P^{n+1})\) are decoupled through a second-order pressure correction scheme [35]. The projection method used here has been analyzed in [36], demonstrating that the scheme achieves second-order accuracy for velocity in \(l^2(0,T;L^2(\Omega ))\), while it is only first-order accurate for pressure in \(l^\infty (0,T;L^2(\Omega ))\). The loss of accuracy for pressure is due to the artificial boundary condition (3.25e)-(3.25f) imposed on pressure [37]. Additionally, we can achieve 1.5 order accuracy for the pressure by using the rotational pressure-correction method [38] based on the Backward difference formula (BDF2) discretization. And the Crank-Nicolson scheme with linear extrapolation is widely regarded as a popular time discretization method for the Navier–Stokes equations. We refer to [36, 38,39,40] and references therein for analysis on this type of discretization.

Next, we prove the unconditional energy stable and MBP of scheme (2).

Theorem 3.3

(Energy stable of the MBP-sESAV2 scheme) The scheme (2) is energy stable in the sense that

$$\begin{aligned} E_h^{n+1}(\Phi , U, S)- E_h^{n}(\Phi , U, S)\le -M\Delta t\Vert W^{n+1/2}\Vert ^2 _{l^2,M} -\nu \Delta t\Vert \frac{D{\varvec{\tilde{U}}}^{n+1} +D{{\textbf{U}}}^{n}}{2}\Vert ^2, \end{aligned}$$
(3.26)

where \({{\textbf{D}}}H=(D_xH,D_yH)\) for any discrete scalar or vector function H, and

$$\begin{aligned} E_h^{n+1}(\Phi , U, S)=\frac{\lambda \epsilon ^2}{2}\Vert {{\textbf{D}}} \Phi ^{n+1} \Vert ^2_{l^2 } +\frac{1}{2}\Vert {{\textbf{U}}}^{n+1}\Vert ^2_{l^2} +\frac{\Delta t^2}{8}\Vert {{\textbf{D}}}P^{n+1} \Vert ^2_{l^2} + S^{n+1}. \end{aligned}$$

Furthermore, it is ensured that \(S^{n}\le {{\mathcal {E}}}_h[\Phi _{init}, {{\textbf{U}}}_{init}]\) and \(S^{\star ,n+\frac{1}{2}}\le {{\mathcal {E}}}_h[\Phi _{init}, {{\textbf{U}}}_{init}]\).

Proof

Multiplying (3.25a) by \(W^{n+1/2} _{i+1/2,j+1/2}h_xh_y\) and taking summation over i, j for \(0\le i \le N_x-1,\ 0 \le j \le N_y-1\) yields

$$\begin{aligned} \begin{aligned}&( \frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t},W^{n+1/2})_{l^2, M}\\&\quad +\chi ^{\star ,n+1/2}\left( \left( \Pi _h \left( U_1^{\star ,n+1/2}\right) \nabla _x +\Pi _h\left( U_2^{\star ,n+1/2}\right) \nabla _y \right) \Phi ^{n+1/2},W^{n+1/2}\right) _{l^2, M}\\&\quad =-{{\mathcal {M}}}\Vert W^{n+1/2}\Vert _{l^2}^2. \end{aligned} \end{aligned}$$
(3.27)

Multiplying (3.25b) by \(\frac{(\Phi ^{n+1} -\Phi ^{n}) _{i+1/2,j+1/2}}{\Delta t}h_xh_y\) and taking summation on i, j over \(0\le i \le N_x-1,\ 0 \le j \le N_y-1\), we arrive at

$$\begin{aligned} (\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t}, W^{n+1/2})_{l^2, M}=&-\lambda \epsilon ^2(d_x D_x \Phi ^{n+1/2}+d_y D_y \Phi ^{n+1/2},\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t})_{l^2, M}\\&- \lambda \chi ^{\star ,n+1/2} \left( {{\bar{f}}}(\Phi ^{\star ,n+1/2}),\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t}\right) _{l^2, M}\\&+\frac{\kappa \lambda \chi ^{\star ,n+1/2}}{\Delta t}\left( \Phi ^{n+1/2}-\Phi ^{\star ,n+1/2},\Phi ^{n+1}-\Phi ^{n}\right) _{l^2, M}. \end{aligned}$$

Recalling Lemma 3.1, we rewrite the first term on the right-hand side of (3.28) as

$$\begin{aligned} \begin{aligned}&-(d_x D_x \Phi ^{n+1/2}+d_y D_y \Phi ^{n+1/2},\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t})_{l^2, M}\\&\quad =( D_x \Phi ^{n+1/2},\frac{D_x \Phi ^{n+1}-D_x \Phi ^{n}}{\Delta t})_{l^2, T, M} +(D_y \Phi ^{n+1/2},\frac{D_y \Phi ^{n+1}-D_y \Phi ^{n}}{\Delta t})_{l^2, M,T}\\&\quad = \frac{\Vert {{\textbf{D}}} \Phi ^{n+1} \Vert _{l^2}^2-\Vert {{\textbf{D}}} \Phi ^{n} \Vert _{l^2}^2}{2\Delta t}. \end{aligned} \end{aligned}$$

Now combining the above identities we obtain

$$\begin{aligned} (\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t}, W^{n+1/2})_{l^2, M}&=\frac{\Vert {{\textbf{D}}} \Phi ^{n+1} \Vert _{l^2}^2-\Vert {{\textbf{D}}} \Phi ^{n} \Vert _{l^2}^2}{2\Delta t}\nonumber \\&\quad - \chi ^{\star ,n+1/2} \left( {{\bar{f}}}(\Phi ^{\star ,n+1/2}),\frac{\Phi ^{n+1}-\Phi ^{n}}{\Delta t}\right) _{l^2, M}\nonumber \\&\quad +\frac{\kappa \chi ^{\star ,n+1/2}}{\Delta t}\left( \Phi ^{n+1/2}-\Phi ^{\star ,n+1/2},\Phi ^{n+1}-\Phi ^{n}\right) _{l^2, M}.\nonumber \\ \end{aligned}$$
(3.28)

Multiplying (3.25c) by \((\frac{{{\tilde{U}}}^{n+1}_1+U^{n}_1}{2})_{i,j+1/2}h_xh_y\), and taking summation over i, j for \(1 \le i \le N_x-1\), \(0 \le j \le N_y-1\), we have

$$\begin{aligned} \begin{aligned}&\frac{1}{2\Delta t}(\Vert {{\tilde{U}}}_1^{n+1}\Vert ^2_{l^2, T, M}-\Vert U_1^{n}\Vert ^2_{l^2, T, M}) +\chi ^{\star ,n+1/2}(C_1^{\star ,n+1/2},\frac{{{\tilde{U}}}^{n+1}_1+U^{n}_1}{2})_{l^2, T, M}\\&\quad +\nu \Vert \frac{d_x {{\tilde{U}}}^{n+1}_1+d_x U^{n}_1}{2}\Vert _{l^2, M} +\nu \Vert \frac{D_y{{\tilde{U}}}^{n+1}_1+D_yU^{n}_1}{2}\Vert _{l^2, T_y}\\&\quad -(P^{n}, \frac{d_x{{\tilde{U}}}^{n+1}_1+d_xU^{n}_1}{2})_{l^2, M} -(\Pi _hW^{n+1/2}D_x \Phi ^{n+1/2},\frac{{{\tilde{U}}}^{n+1}_1+U^{n}_1}{2})_{l^2, T, M}=0. \end{aligned} \end{aligned}$$
(3.29)

Multiplying (3.25d) by \((\frac{{{\tilde{U}}}^{n+1}_2+U^{n}_2}{2})_{i+1/2,j}h_xh_y\), and taking summation over i, j for \(0 \le i \le N_x-1\), \(1 \le j \le N_y-1\) leads to

$$\begin{aligned} \begin{aligned}&\frac{1}{2\Delta t}(\Vert {{\tilde{U}}}_2^{n+1}\Vert ^2_{l^2, M, T}-\Vert U_2^{n}\Vert ^2_{l^2, M, T})+\chi ^{\star ,n+1/2}(C_1^{\star ,n+1/2},\frac{{{\tilde{U}}}^{n+1}_2+U^{n}_2}{2})_{l^2, M, T}\\&\quad +\nu \Vert \frac{d_y {{\tilde{U}}}^{n+1}_2+d_y U^{n}_2}{2}\Vert _{l^2, M} +\nu \Vert \frac{D_x {{\tilde{U}}}^{n+1}_2+D_x U^{n}_2}{2}\Vert _{l^2, T_x}\\&\quad -(P^{n}, \frac{d_y{{\tilde{U}}}^{n+1}_2+d_yU^{n}_2}{2})_{l^2, M} -(\Pi _h W^{n+1/2}D_y \Phi ^{n+1/2},\frac{{{\tilde{U}}}^{n+1}_2+U^{n}_2}{2})_{l^2, M, T}=0. \end{aligned} \end{aligned}$$
(3.30)

It follows directly from (3.25e)-(3.25f) that

$$\begin{aligned} \frac{1}{2\Delta t}\Vert {{\textbf{U}}}^{n+1}-{\varvec{\tilde{U}}}^{n+1}\Vert ^2_{l^2} =\frac{\Delta t}{8}\Vert {{\textbf{D}}}P^{n+1}-{{\textbf{D}}}P^n\Vert ^2_{l^2}. \end{aligned}$$
(3.31)

Taking discrete inner products of (3.25e)-(3.25f) with \(U^{n+1}_{1,i,j+1/2}h_xh_y\), \(U^{n+1}_{2,i+1/2,j}h_xh_y\) respectively, we obtain

$$\begin{aligned} \Vert {{\textbf{U}}}^{n+1}\Vert ^2_{l^2} -\Vert {\varvec{\tilde{U}}}^{n+1}\Vert ^2_{l^2} + \Vert {{\textbf{U}}}^{n+1}-{\varvec{\tilde{U}}}^{n+1}\Vert ^2_{l^2} =0. \end{aligned}$$
(3.32)

We further rewrite the projection step (3.25e)-(3.25f) as

$$\begin{aligned} U_1^{n+1}+U_1^{n}-({{\tilde{U}}}_1^{n+1}+U_1^n) +\frac{\Delta t}{2}(D_xP^{n+1}-D_xP^n)=0, \end{aligned}$$
(3.33a)
$$\begin{aligned} U_2^{n+1}+U_2^{n}-({{\tilde{U}}}_2^{n+1}+U_2^n) +\frac{\Delta t}{2}(D_yP^{n+1}-D_yP^n)=0. \end{aligned}$$
(3.33b)

Taking discrete inner products of (3.33a) and (3.33b) with \(\frac{\Delta t}{2}D_x P^n_{i+1/2,j+1/2}h_xh_y\), \(\frac{\Delta t}{2}D_y P^n_{i+1/2,j+1/2}h_xh_y\) respectively, summing them up, after applying the divergence-free condition (3.25g), it is clear that

$$\begin{aligned} \begin{aligned}&(D_xP^n,\frac{{{\tilde{U}}}^{n+1}_1+U^{n}_1}{2})_{l^2,T,M} + (D_yP^n,\frac{{{\tilde{U}}}^{n+1}_2+U^{n}_2}{2})_{l^2,M,T}\\&=\frac{\Delta t}{8}[\Vert {{\textbf{D}}} P^{n+1}\Vert ^2_{l^2} - \Vert {{\textbf{D}}} P^{n}\Vert ^2_{l^2} -\Vert {{\textbf{D}}} P^{n+1}-{{\textbf{D}}} P^{n}\Vert ^2_{l^2} ]. \end{aligned} \end{aligned}$$
(3.34)

Combining Eqs. (3.27)–(3.32) with (3.34) and (3.25k) and noting (3.25g), similar to that of Theorem 3.1 gives the desired result (3.26).

The uniform upper bound of \(\{S^n\}\) can be regarded as a direct result of the energy dissipation, which can be established through a procedure similar to that outlined in the proof of Corollary 3.1. Notice that from Theorem 3.1, we know

$$\begin{aligned} S^{\star ,n+\frac{1}{2}}\le E_h[\Phi ^{\star ,n+\frac{1}{2}},{{\textbf{U}}}^{\star ,n+\frac{1}{2}},S^{\star ,n+\frac{1}{2}}]\le E_h[\Phi ^{n},{{\textbf{U}}}^n,S^{n}], \end{aligned}$$

and hence, we also have \(S^{\star ,n+\frac{1}{2}}\le {{\mathcal {E}}}_h[\Phi _{init}, {{\textbf{U}}}_{init}]\), as \(S^{\star ,n+\frac{1}{2}}\) is generated by the pressure-correction sESAV1 scheme (1). \(\square \)

Theorem 3.4

(Discrete MBP of the MBP-sESAV2 scheme) If f be continuously differentiable on \([-\beta , \beta ]\) and \(\kappa \ge \Vert f'\Vert _{C[ - \beta ,\beta ]}\), assume

$$\begin{aligned} h\le \frac{2\lambda \epsilon ^2{{\mathcal {M}}}}{{{\hat{C}}} G^*} ~~\text {and}~~ \Delta t\le (\frac{G^*{{\mathcal {M}}}\lambda \kappa }{2} +\frac{{{\mathcal {M}}}\lambda \epsilon ^2}{h^2})^{-1}, \end{aligned}$$
(3.35)

where \({{\hat{C}}}>0\) is defined in Remark 3.2 and \(G^*=\exp \left\{ {{\mathcal {E}}}_h\left( \Phi _{\text{ init }}, {{\textbf{U}}}_{\text{ init }}\right) +C_*\right\} \), then the MBP-sESAV2 scheme (2) preserves the MBP unconditionally.

Proof

Suppose \((\Phi ^n, S^n)\) is given and \(\left\| \Phi ^n\right\| _{L^{\infty }(\Omega )}\le \beta \) for some n. From (3.25a)-(3.25b), we have

$$\begin{aligned} \begin{aligned} \left( (\frac{2}{\Delta t}+{{\mathcal {M}}}\lambda \kappa \chi ^{\star ,n+1/2})I -{{\mathcal {L}}}_{{{\textbf{U}}}^\star }\right) \Phi ^{n+1}&= \left( (\frac{2}{\Delta t}-{{\mathcal {M}}}\lambda \kappa \chi ^{\star ,n+1/2})I +\mathcal {L^\star _{{{\textbf{U}}}}}\right) \Phi ^{n}\\&\quad +2{{\mathcal {M}}}\lambda \chi ^{\star ,n+1/2}\left( {{\bar{f}}}(\Phi ^{\star ,n+1/2})+\kappa \Phi ^{\star ,n+1/2}\right) , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} {{\mathcal {L}}}_{{{\textbf{U}}}^\star }={{\mathcal {M}}}\lambda \epsilon ^2(d_x D_x +d_y D_y )-\chi ^{\star ,n+1/2}\left( \Pi _h \left( U_1^{\star ,n+1/2}\right) \nabla _x +\Pi _h\left( U_2^{\star ,n+1/2}\right) \nabla _y \right) . \end{aligned} \end{aligned}$$

Noticing Theorems 3.1 and 3.3, it follows that \(\left\| \Phi ^{\star ,n+1/2}\right\| _{L^{\infty }(\Omega )}\le \beta \) and \(S^{\star ,n+\frac{1}{2}}\le {{\mathcal {E}}}_h[\Phi _{init}, {{\textbf{U}}}_{init}]\). Consequently, we deduce that \(0<\chi ^{\star ,n+1/2}\left( \Phi , S\right) \le G^*\) through a similar analysis as demonstrated in Theorems 3.2. If the inequality

$$\begin{aligned} h \max \left\{ \left\| U^{\star ,n+1/2}_{1,i,j}\right\| _{L^\infty }, \left\| U^{\star ,n+1/2}_{2,i,j}\right\| _{L^\infty } \right\} \le h{{\hat{C}}} \le \frac{2\lambda \epsilon ^2{{\mathcal {M}}}}{G^*}, \end{aligned}$$
(3.36)

is satisfied, then \({{\mathcal {L}}}_{{{\textbf{U}}}^\star }\) is a negative diagonally dominant matrix, and the coefficient matrix of (3.25a)-(3.25b) satisfies the conditions of Lemma  2.1. Now (3.35) implies

$$\begin{aligned} \frac{2}{\Delta t}-{{\mathcal {M}}}\lambda \kappa \chi ^{\star ,n+1/2}\ge \frac{2{{\mathcal {M}}}\lambda \epsilon ^2}{h^2}. \end{aligned}$$

Note that

$$\begin{aligned} \left\| \left( \frac{2}{\Delta t}-{{\mathcal {M}}}\lambda \kappa \chi ^{\star ,n+1/2}\right) I +{{\mathcal {L}}}_{{{\textbf{U}}}^\star } \right\| _{L^{\infty }(\Omega )}= \frac{2}{\Delta t}-{{\mathcal {M}}}\lambda \kappa \chi ^{\star ,n+1/2}. \end{aligned}$$

Due to \(\kappa \ge \Vert f'\Vert _{C[ - \beta ,\beta ]}\) and Lemma 2.2, we have \(\left\| {{\bar{f}}}(\Phi ^{\star ,n+1/2})+\kappa \Phi ^{\star ,n+1/2}\right\| _{L^{\infty }(\Omega )} \le \kappa \beta .\) Thus, under the condition specified in (3.35) and using Lemma 2.1, we derive

$$\begin{aligned} \left\| \Phi ^{n+1}\right\| _{L^{\infty }(\Omega )}&\le \left( \frac{2}{\Delta t}+{{\mathcal {M}}}\lambda \kappa \chi ^{\star ,n+1/2}\right) ^{-1}\\&\quad \left[ \left( \frac{2}{\Delta t}-{{\mathcal {M}}}\lambda \kappa \chi ^{\star ,n+1/2}\right) \beta +2{{\mathcal {M}}}\kappa \lambda \chi ^{\star ,n+1/2}\beta \right] = \beta , \end{aligned}$$

then we have \(\left\| \Phi ^{n}\right\| _{L^{\infty }(\Omega )}\le \beta \) by induction for all n. \(\square \)

Remark 3.4

The condition given by (3.35) on the time step size implies that \(\Delta t= O(h^2/{{\mathcal {M}}}\lambda \epsilon ^2)\). In practical computations, we observe that \(\chi ^{\star ,n+1/2}\approx 1\), which allows us to set a requirement for the time step size as \(\Delta t\le (\frac{{{\mathcal {M}}}\lambda \kappa }{2} +\frac{{{\mathcal {M}}}\lambda \epsilon ^2}{h^2})^{-1}\) in order to preserve the MBP, as utilized in our subsequent numerical experiments.

4 Numerical Simulations

In this section, we provide some numerical experiments to validate our theoretical results and the MBP-preserving properties of the constructed schemes for the conserved ACNS model. Unless otherwise specified, we adopt \(C_*=1\) and the Flory-Huggins potential (2.6) with the parameters \(\theta =0.8\) and \(\theta _c=1.6\) for the simulation. If f is the double-well potential function (2.5), we choose \(\kappa = 3\) as the stabilizing coefficient, whereas if it is the Flory-Huggins potential function (2.6), we set \(\kappa = 28.87\). In addition, we take \(\sigma (x)=\exp (x)\) for \(\sigma (x)\) in (2.12).

4.1 Convergence Tests

We test the convergence in two dimensions, with the Flory-Huggins potential function f defined in (2.5). The model parameters are taken as follows:

$$\begin{aligned} {{\mathcal {M}}}=0.001,\quad \lambda =2, \quad \epsilon ^2=0.1, \quad \nu =0.1,\quad L_x =L_y =1, \quad \kappa =0. \end{aligned}$$

We choose right-hand sides of (1.1) suitably such that the exact solution is given by:

$$\begin{aligned} \begin{aligned} \phi (x,y,t)&=\cos (t)\cos (\pi x)\cos (\pi y),\\ {{\textbf{u}}}(x,y,t)&=0.1\sin (t)(sin^2(\pi x)\sin (2\pi y), -sin(2\pi x)\sin ^2(\pi y)),\\ p(x,y,t)&=\sin (t)(sin(\pi y)-2/\pi ). \end{aligned} \end{aligned}$$

Example 1

(Refinement in space) We first test convergence rates the of the first- and second-order schemes in space. The reference solution is computed using the time step of \(\Delta t=10^{-5}\). The errors at \(T = 0.5\), measured in the \(L^2\) norm with varying space steps, are presented in Fig. 1, distinctly demonstrating the second-order convergence in the spatial dimension.

Fig. 1
figure 1

Numerical convergence rate of the first-(left) and second-order schemes (right)

Full size image

Example 2

(Refinement in time) Next, we use \(256\times 256\) modes to discretize the space variables so that the spatial discretization error is negligible compared to the time discretization. In Fig. 2, we list the errors of the phase variable \(\phi \), the velocity \({{\textbf{u}}}\), and the pressure p between the numerical and the exact solution at \({T=0.128}\). It can be observed that our schemes match the expected accuracy in time perfectly well.

Fig. 2
figure 2

Numerical convergence rate of the first-(left) and second-order schemes (right)

Full size image

4.2 MBP Tests for the Flow-Coupled Phase Separation

In this example, we perform the numerical simulations of spinodal decomposition in a two-dimensional setting. The simulations are carried out on \([0, L]^2\) with \(L = 1.0\). We test the MBP-sESAV2 scheme with a spatial mesh size of \(h = 1/100\) and a time step size \(\Delta t=10^{-3}\).

The initial condition is a random state, in which a random number ranging from \(-0.9\) to 0.9 is assigned to each grid point. Moreover, both the double-well potential function (2.5) and the Flory-Huggins potential function (2.6) are discussed here. We choose the parameters for Fig. 3 and Fig. 4a–c as follows:

$$\begin{aligned} {{\mathcal {M}}}=0.5,\quad \lambda =100, \quad \epsilon =0.01, \quad \nu =1.0. \end{aligned}$$
(4.39)

In Fig. 3, a comparison of two simulations produced by the two different potentials shows that the evolution processes are overall similar. It can be observed that the discrete MBP holds, and the energy decays monotonically with time in Fig. 4a–c. The red solid lines represent \(y=\beta =2\sqrt{3}/3\) and \(y=\beta \approx 0.9868\), respectively, which are the theoretical maximum bound [18, 27] for the double-well potential function and the Flory-Huggins potential function. In Fig. 4d, we investigate unconditional stability by setting \({{\mathcal {M}}}=0.15\), \(\lambda =100\), \(\epsilon =0.03\), \({\nu =1.0}\) and \(\kappa =0\) with MBP-sESAV1 scheme, while employing various time step sizes with \(\Delta t =1,\ 0.1,\ 0.01\). Our results confirm that the modified energy consistently decreases, as demonstrated in Theorem 3.1 and Theorem 3.3. In addition, we observe that the original energy oscillates slightly with \(\Delta t=1\), while the modified energy consistently shows a decreasing trend. This further validates that our scheme can achieve modified energy dissipation even with large time steps.

Fig. 3
figure 3

Snapshots of the phase function \(\phi \) at \(t=0.2,\ 1.1,\ 5,\ 10\) for the ACNS model (1.1) with the double-well potential (top) and the Flory-Huggins potential (bottom) in two dimensions

Full size image
Fig. 4
figure 4

Evolutions of the supremum norm (a)(b) and energies (c) for the ACNS model (1.1) with both the double-well potential (2.5) and the Flory-Huggins potential (2.6). d depicts the evolution of energies for the double-well potential (2.5)

Full size image

4.3 Shape Relaxation

In this simulation, we adopt a star-shaped interface evolution with the initial value given by

$$\begin{aligned} \begin{aligned}&\phi (x,y,0)=0.9\tanh \frac{0.25+0.1cos(a\theta )-r}{\sqrt{2}\epsilon },\\&\theta =\arctan \frac{y-0.5}{x-0.5},\quad r=\sqrt{(x-0.5)^2+(y-0.5)^2}. \end{aligned} \end{aligned}$$
(4.40)

The parameter a represents the number of vertices of the initial data. We discretize the space variables with \(100\times 100\) modes, and choose the values of parameters as

$$\begin{aligned} \begin{aligned} \Delta t=0.001,\quad \lambda =100, \quad {{\mathcal {M}}}=0.5,\quad \epsilon =0.01,\quad \nu =1.0, \quad L_x =L_y =1.0. \end{aligned} \end{aligned}$$

In Fig. 5, we depict the dynamic process of shape relaxation towards a disk by setting different values of a in (4.40). As indicated in [41,42,43], it can be clearly observed from Fig. 6 that the larger value of a (indicating more vertices of the initial data), the faster rate of the evolution process, which is consistent with the findings in Fig. 5. It appears that the interfacial thickness, approximated to the distance between contours \(\phi =-0.8\) and \(\phi =0.8\), remains constant with different a. The evolutions of the supremum norm of \(\phi \) and the energy of the simulated solutions are displayed in Fig. 6. One can also observe that the discrete MBP is well preserved, and the energy decays monotonically.

Fig. 5
figure 5

Snapshots of the phase function \(\phi \) with contours \(\phi =-0.8,\ 0,\ 0.8\) for \(a= 6,\ 10,\ 14\) at \(t=0.01,\ 0.1,\ 0.2,\ 1\) respectively

Full size image
Fig. 6
figure 6

Time evolutions of supremum norms (left) and energies(right) for different a

Full size image

4.4 Buoyancy-Driven Flow

In this example, we modify the momentum Eq. (1.1c) by adding the following buoyancy term on the right-hand side of (1.1c)

$$\begin{aligned} \begin{aligned} b(\phi ){{\textbf{g}}}=G(\rho (\phi )-{{\tilde{\rho }}}){{\textbf{g}}} =G\frac{\phi _1-\phi _2}{2}(\phi -{\bar{\phi }}){{\textbf{g}}}:=\chi (\phi -{\bar{\phi }}){{\textbf{g}}}, ~ {{\textbf{g}}}=(0,1)^{T}, \end{aligned} \end{aligned}$$

where \({\bar{\phi }}\) represents the spatially averaged parameter. Thus one obtains

$$\begin{aligned} \frac{\partial {{\textbf{u}}}}{\partial t}+ {{\textbf{u}}}\cdot \nabla {{\textbf{u}}} -\nu \Delta {{\textbf{u}}}+\nabla p= \mu \nabla \phi +\chi (\phi -{\bar{\phi }}){{\textbf{g}}}. \end{aligned}$$
(4.41)

The computational domain is \(\Omega = [0, 1]^2\), and we use \(100\times 100\) modes to discretize the space variables. The numerical parameters are set as follows:

$$\begin{aligned} \begin{aligned} \Delta t=0.001, \quad \lambda =10, \quad \epsilon =0.01. \end{aligned} \end{aligned}$$

Example 3

(Bubble rising) The phase function is initialized with a circular bubble positioned at the center of the domain at the coordinates (0.5, 0.25), and the initial velocity is set to \(u_0 = 0\). The top pictures given in Fig. 7 present snapshots of the phase evolution at different time points \((t = 1.0, 6.0, 10.0, 13.1)\). Initially, the bubble is observed as a circular shape located near the lower region of the domain. As the bubble, which possesses a lower density compared to the surrounding fluid, rises gradually, it undergoes a transition into an elliptical shape and eventually deforms as it approaches the upper boundary, as expected in the refercence [34]. Additionally, streamline visualizations of velocities are provided in the bottom of Fig. 7.

Fig. 7
figure 7

Snapshots of the phase function \(\phi \) (top) and velocity field (bottom) with \(\nu =1\), \(\chi =10\) and \({{\mathcal {M}}}=5.0\) for bubble rising at different time \(t=1.0,\ 6.0,\ 10.0,\ 13.1\)

Full size image

Example 4

(Dripping droplet) We commence by conducting simulations to investigate the dynamic behavior of a dripping droplet under different Reynolds numbers, namely \(\nu = 1/10\) and 1/20. Initially, the droplet, which has a heavier density compared to its surrounding medium (e.g., air), adheres to the upper solid wall. Due to the influence of gravity with \(\chi =50\), the droplet gradually falls. In Fig. 8, the first row displays the snapshots of the droplet for \(\nu = 1/10\), while the top row in Fig. 9 depicts the evolution results for \(\nu = 1/20\). It is evident that as the Reynolds number \(1/\nu \) increases, the pinch-off process occurs more rapidly and the droplet falls more quickly. Furthermore, the velocity streamlines are presented in the bottom row of Figs. 8 and 9. It can be seen that the formation of spike structures becomes more evident, especially when the liquid filament is extensively elongated. These simulations are consistent with the experimental presented in [44] and the simulations demonstrated in [5, 45]. High temporal accuracy can be achieved in the MBP-sESAV2 scheme by utilizing a time step \(\Delta t=0.001\), which is a noteworthy result. In Fig. 10, we again observe that the MBP for the ACNS model with (4.41) is numerically well-preserved.

Fig. 8
figure 8

Snapshots of the phase function \(\phi \) (top) and velocity field (bottom) with \(\nu =0.1\) and \({{\mathcal {M}}}=1.0\) for dripping droplet at different time \(t=0.2,\ 0.3,\ 0.5,\ 0.6\)

Full size image
Fig. 9
figure 9

Snapshots of the phase function \(\phi \) (top) and velocity field (bottom) with \(\nu =0.05\) and \({{\mathcal {M}}}=1.0\) for dripping droplet at different time \(t=0.2,\ 0.3,\ 0.4,\ 0.5\)

Full size image
Fig. 10
figure 10

Time evolutions of supremum norms: bubble rising with \(\nu =1,\ \chi =10\) (left), dripping droplet with \(\nu =0.1, \chi =50\) (middle), and \(\nu =0.05,\ \chi =50\) (right)

Full size image

5 Concluding Remarks

We develope efficient numerical schemes, both first- and second-order, to solve the hydrodynamically coupled mass-conserved Allen-Cahn phase-field model for a two-phase flow system. These schemes are constructed by combining the projection method for the Navier-Stokes equation and the generalized stabilized exponential scalar auxiliary variable approach for the decoupling of the nonlinear terms. The proposed schemes possess several desirable properties, including linearity, second-order accuracy in space and time, complete decoupling and particularly the preservation of the MBP. In addition, we also demonstrate the unconditional energy dissipation based on the generalized stabilized exponential scalar auxiliary variable approach. Furthermore, we provide a rigorous proof of the preservation of the MBP for both schemes.