A Bayesian Framework for Spectral Reprojection

Abstract

Fourier partial sum approximations yield exponential accuracy for smooth and periodic functions, but produce the infamous Gibbs phenomenon for non-periodic ones. Spectral reprojection resolves the Gibbs phenomenon by projecting the Fourier partial sum onto a Gibbs complementary basis, often prescribed as the Gegenbauer polynomials. Noise in the Fourier data and the Runge phenomenon both degrade the quality of the Gegenbauer reconstruction solution, however. Motivated by its theoretical convergence properties, this paper proposes a new Bayesian framework for spectral reprojection, which allows a greater understanding of the impact of noise on the reprojection method from a statistical point of view. We are also able to improve the robustness with respect to the Gegenbauer polynomials parameters. Finally, the framework provides a mechanism to quantify the uncertainty of the solution estimate.

1 Introduction

Fourier samples model data acquisitions in applications such as magnetic resonance imaging (MRI) and synthetic aperture radar (SAR). Indeed, recovering images from either MRI k-space data or SAR phase history data most often involves recasting the problem as a linear inverse problem with the forward operator given by the discrete (non-uniform) Fourier transform (DFT) matrix (see e.g. [3, 4, 24, 30, 36]). Compressive sensing (CS) algorithms that promote sparse solutions in a known sparse domain [6, 16, 17, 34] have become increasingly widespread in providing point estimate image recoveries. More recently, Bayesian inference methods have been developed to also quantify the uncertainty of the estimate.

This investigation develops a new Bayesian framework for recovering smooth but non-periodic functions from given noisy Fourier data. Uncertainty quantification can also be achieved when the hyperparameters in the posterior density function are fixed. Importantly, however, rather than use the often employed sparse prior (or sparse penalty term in CS), here we construct a prior based on spectral reprojection [26, 27].

The spectral reprojection method is a forward approach designed to reproject the observable Fourier data onto a Gibbs complementary basis. It is sometimes referred to as Gegenbauer reconstruction when the Gibbs complementary basis is comprised of Gegenbauer polynomials. The reprojection eliminates the Gibbs phenomenon and restores the exponential convergence (hence the use of spectral in its name) in the maximum norm. For self-containment, we summarize spectral reprojection in Sect. 2.2.

Although Gegenbauer reconstruction has been successfully used in applications where the observable Fourier data have complex additive Gaussian noise of mean zero [3, 43], it was also demonstrated in [5] that while the estimator is unbiased, its variance is spatially dependent. Nevertheless, theoretical results in the seminal work [27] provide key insights that inspire us to develop a new Bayesian inference method for the corresponding inverse problem. Namely, the derivation of the error terms in the exponential convergence proof naturally motivates the choices of the likelihood and prior terms in the Bayesian method. In particular, the prior used for the construction of the posterior should be designed to favor solutions whose orthogonal polynomial partial sum expansion yields good approximations. Such an assumption is consistent for recovering (discretized) functions that are smooth but not periodic, and is arguably more appropriate than using a sparsifying operator such as first order differencing, which by design assumes that the underlying function is piecewise constant, or Tikhonov regularization, which is even more restrictive. Moreover, when coupled with the likelihood term, the common kernel condition [32] is automatically satisfied so that a unique minimum for the corresponding maximum a posteriori (MAP) estimate may be obtained. We call this approach the Bayesian spectral reprojection (BSR) method, and its point estimate solution, which is consistent with Gegenbauer reconstruction, is the MAP estimate of the corresponding posterior density and is determined through optimization. As already noted, we are also able to provide uncertainty quantification for fixed hyperparameters.

We further propose a generalized Bayesian spectral reprojection (GBSR) method, which modifies the BSR by formulating the likelihood so that the observables are not first transformed to the Gibbs complementary basis. Rather, we directly use the observable Fourier data for this purpose. Removing this restriction allows us to explore a larger space that still assumes that the function is well-approximated by the Gegenbauer partial sum expansion, but also seeks a good fit to the observable data. As our numerical results demonstrate, the point estimate obtained using GBSR is more robust in low signal-to-noise ratio (SNR) environments to different parameter choices. It is also possible to quantify the uncertainty when the posterior density function uses fixed hyperparameters.

1.1 Paper organization

The rest of this paper is organized as follows. Section 2 describes the underlying problem and summarizes the spectral reprojection method [26]. The problem is then discretized in Sect. 3 to enable the Bayesian approach used in Sect. 4. There we describe how the theoretical results proving exponential convergence for spectral reprojection inspire the construction of a new prior, leading to the Bayesian spectral reprojection (BSR) method. These ideas are then modified in Sect. 5 for the generalized Bayesian spectral reprojection (GBSR) method. Numerical examples in Sect. 6 show the efficacy of our new methods for recovering 1D smooth functions from noisy Fourier data. Section 7 provides some concluding remarks.

2 Preliminaries

Let f be a real-valued analytic $L^2$ integrable function on $[-1,1]$. We are given its first N (for convenience we choose N to be even) noisy Fourier measurements $\widehat{{\textbf{b}}} \in {\mathbb {C}}^N$ with components

$$\begin{aligned} \widehat{b}_k = \widehat{f}_k + \widehat{\epsilon }_k, \quad \quad k = -\frac{N}{2}, \ldots , \frac{N}{2} -1, \end{aligned}$$

(2.1)

where

$$\begin{aligned} \widehat{f}_k = \frac{1}{2}\int _{-1}^1 f(x) e^{-ik\pi x} \,dx, \end{aligned}$$

(2.2)

and the components $\widehat{\epsilon }_k \sim {\mathcal {C}}{\mathcal {N}}(0,\alpha ^{-1})$ of $\widehat{\varvec{\epsilon }} \in {\mathbb {C}}^N$ each follows a circularly-symmetric complex normal distribution with unknown variance $\alpha ^{-1}>0$. The noiseless Fourier partial sum approximation

$$\begin{aligned} S_N f(x) = \sum _{k = -\frac{N}{2}}^{\frac{N}{2}-1} \widehat{f}_ke^{ik\pi x} \end{aligned}$$

(2.3)

yields the infamous Gibbs phenomenon for non-periodic f [25], notably manifested by the spurious oscillations at the boundaries $x = \pm 1$ as well as an overall reduced order of convergence away from the boundaries. We note that the Gibbs phenomenon also occurs whenever f is piecewise smooth with spurious oscillations forming near internal discontinuity locations. When these locations are known in advance the techniques introduced in this investigation can be straightforwardly adapted via linear transformation. When they are unknown, methods such as those in [19, 40] can be first applied to find them. Thus to simplify our presentation we will only consider non-periodic analytic $L^2$ integrable functions on $[-1,1]$.

2.1 Resolution of the Gibbs Phenomenon

The Gibbs phenomenon has been extensively studied for a variety of applications. While the purpose of this investigation is neither to survey nor compare the myriad techniques developed to resolve it, we describe a few well-known methods for context.

Spectral filters (see e.g. [42]) provide the most straightforward and cost efficient approach for mitigating the Gibbs phenomenon, but cause fine details of the solution to be “smoothed out” at the boundaries of non-periodic smooth functions. Another forward method is spectral reprojection, first introduced in [27], which can more sharply resolve the approximation by first reprojecting (2.3) into a more suitable basis. The inverse polynomial reconstruction method in [38] and least squares method developed in [2] (which is designed for general samples in a separable Hilbert space) can sometimes better resolve the Gibbs phenomenon, but there is a trade-off between stability and increased points-per-wave requirement. Convex optimization approaches using $\ell _1$ regularization, commonly referred to as compressive sensing algorithms (e.g. [6]) have also been used successfully. Each of these methods requires parameter tuning, which becomes increasingly difficult as more noise is prevalent in the data. Moreover, they are not designed to quantify the uncertainty of the solution. This is particularly problematic since different parameter choices can sometimes lead to wildly different approximations. Finally we mention the statistical filter method developed in [39] which constructs the approximation from the given Fourier data by minimizing the error over a set of possible reconstructions. Although the approach is Bayesian, it does not provide any uncertainty quantification. Our goal here is therefore to develop a Bayesian approach that (1) accurately approximates a smooth but non-periodic function in $[-1,1]$ on a chosen set of pixels given a finite number of its noisy Fourier coefficients, and (2) quantifies the uncertainty in the approximation.

2.2 Spectral Reprojection

In a nutshell, spectral reprojection reprojects $S_N f$ in (2.3) onto a more suitable Gibbs complementary basis. Under certain parameter constraints, the Gegenbauer polynomials serve as a reprojection basis that ensures exponential accuracy in the maximum norm without significantly increasing the points-per-wave requirement. These constraints eliminate both Chebyshev and Legendre polynomials as suitable.¹ Below we provide a brief synopsis as it pertains to our investigation. An in depth review of spectral reprojection and its convergence analysis may be found in [26].

In order to achieve exponential accuracy, the reprojection basis must have the property that the high modes of the Fourier basis have exponentially small projections onto its low modes. Let the polynomial basis $\left\{ \psi ^\lambda _l \right\}$, with the parameter $\lambda \in {\mathbb {R}}^+$ corresponding to a prescribed weight function $w_\lambda$ and index $l \in {\mathbb {Z}}^+ \cup \{0\}$ corresponding to its degree, be such a basis. The mth-degree polynomial approximation of a function f using $\left\{ \psi ^\lambda _l \right\} _{l = 0}^m$ is given by

$$\begin{aligned} P_m^\lambda f(x):= \sum _{l=0}^m \widehat{f}_l^\lambda \psi _l^\lambda (x). \end{aligned}$$

(2.4)

To determine the coefficients $\widehat{f}_l^\lambda$, consider the standard definition for a weighted inner product with respect to the prescribed weight function $w_\lambda$,

$$\begin{aligned} \langle f,g \rangle _{w_\lambda } = \int _{-1}^1 w_\lambda (x) f(x) g(x) dx. \end{aligned}$$

(2.5)

We choose $\left\{ \psi ^\lambda _l \right\} _{l = 0}^m$ to be orthogonal with respect to $w_\lambda$ so that

$$\begin{aligned} \langle \psi ^\lambda _l, \psi ^\lambda _{l^\prime } \rangle _{w_\lambda } = \int _{-1}^1 w_\lambda (x) \psi ^\lambda _l(x) \psi ^\lambda _{l^\prime }(x) dx = {\left\{ \begin{array}{ll} \left\| \psi ^\lambda _l \right\| ^2_{w_\lambda }:=h_l^\lambda & \hbox { if}\ l = l^\prime , \\ 0 & \text{ otherwise }, \end{array}\right. } \end{aligned}$$

(2.6)

where for ease of notation we have defined $h_l^\lambda = \Vert \psi ^\lambda _l \Vert ^2_{w_\lambda }.$ Hence by construction the coefficients $\widehat{f}_\ell ^\lambda$ in (2.4) are determined as

$$\begin{aligned} \widehat{f}^\lambda _l = \frac{\langle f, \psi ^\lambda _l\rangle _{w_\lambda }}{\left\| \psi ^\lambda _l \right\| ^2_{w_\lambda }} = \frac{1}{h_l^\lambda } \int _{-1}^1 w_\lambda (x) f(x) \psi ^\lambda _{l}(x) dx. \end{aligned}$$

(2.7)

An admissible Gibbs complementary basis must first and foremost yield exponential convergence (see e.g. [10, 29]) in the maximum norm as a partial sum expansion for analytic $L^2$ integrable $f \in L^2[-1,1]$ for $\lambda = \beta m$, $\beta > 0$.² That is,

$$\begin{aligned} \max _{-1 \le x \le 1} \left| f(x) - P_m^\lambda f(x) \right| \le Const_1 \cdot e^{-m^r} \end{aligned}$$

(2.8)

for $m>> 1$ and $r > 0$. The significance of the reprojection method lies in the observation that f in (2.4) can be replaced by its N-term Fourier expansion $S_Nf$ in (2.3) yielding

$$\begin{aligned} P_m^\lambda S_Nf(x):= \sum _{l=0}^m \widehat{g}_l^\lambda \psi _l^\lambda (x) \end{aligned}$$

(2.9)

where

$$\begin{aligned} \widehat{g}_l^\lambda = \frac{\langle S_Nf, \psi _l^\lambda \rangle _{w_\lambda }}{\left\| \psi _l^\lambda \right\| ^2_{w_\lambda }} = \frac{1}{h_l^\lambda }\int _{-1}^1 w_\lambda (x) S_Nf(x) \psi ^\lambda _{l}(x) dx, \end{aligned}$$

while still retaining exponential reconstruction accuracy in the maximum norm on $[-1,1]$. That is,

$$\begin{aligned} \max _{-1 \le x \le 1} \left| f(x) - P_m^\lambda S_Nf(x) \right| \le Const_2 \cdot e^{-m^p}, \end{aligned}$$

(2.10)

for $m>> 1$ and $p > 0$. Satisfying (2.10) requires that $m = \kappa N$ for some admissible $\kappa < 1$ (see Theorem 1 below). This is a profound statement which says that a poorly converging N-term Fourier expansion contains sufficient information to recover and approximate the function with exponential accuracy. The form of (2.9) gives the method its name – the Fourier partial sum approximation is reprojected to a Gibbs complementary basis yielding spectral accuracy.

2.3 Gegenbauer Polynomials

Mainly due to straightforward analysis and convenient closed form equations that can be used directly in numerical implementation, the most commonly employed Gibbs complementary basis is the family of Gegenbauer polynomials, $\{C^\lambda _l(x)\}_{l = 0}^m$. We use them here as well, and note that for robustness purposes, in some cases it might be beneficial to instead use the Freud polynomials [20] (see Remark 6.1). We also point out that there is no inherent constraint that the reprojection basis need be polynomials. We now proceed to provide the definition of the Gegenbauer polynomials. As in [27], we rely on [7] for several of the corresponding explicit formulae.

Definition 2.1

The Gegenbauer polynomial $C_l^{\lambda }(x)$, $\lambda \ge 0$, is the polynomial of degree l that satisfies

$$\begin{aligned} \int _{-1}^{1} w_\lambda (x) C_k^{\lambda }(x) C_l^{\lambda }(x) dx=0, \qquad k\ne l, \end{aligned}$$

where $w_\lambda (x) = (1-x^2)^{\lambda -\frac{1}{2}}$ is the corresponding weight function. The normalizing term $h_l^\lambda$ in (2.7) is explicitly given by

$$\begin{aligned} h_l^\lambda =\pi ^{\frac{1}{2}}C_l^{\lambda }(1)\frac{\varGamma (\lambda +\frac{1}{2})}{\varGamma (\lambda )\varGamma (l+\lambda )}. \end{aligned}$$

(2.11)

Here $C_l^{\lambda }(1)=\frac{\varGamma (l+2\lambda )}{l!\varGamma (2\lambda )}$ and $\varGamma (\lambda )$ denotes the usual gamma function.

By substituting $C^\lambda _l(x)$ into (2.4), we obtain the Gegenbauer partial sum expansion

$$\begin{aligned} P_m^{\lambda }f(x) = \sum _{l=0}^{m} \widehat{f}^{\lambda }_{l}\, C^\lambda _l(x), \end{aligned}$$

(2.12)

with Gegenbauer coefficients in (2.7) provided by

$$\begin{aligned} \widehat{f}^{\lambda }_{l}=\frac{1}{h^\lambda _l} \int _{-1}^{1}(1-x^2)^{\lambda -\frac{1}{2}}\,f(x)\,C^\lambda _l(x)dx. \end{aligned}$$

(2.13)

Note that (2.12) converges exponentially in the sense of (2.8) for f analytic in $[-1,1]$ and $\lambda \ge 0$ [10, 29]. In particular, Chebyshev ($\lambda = 0$) and Legendre ($\lambda = \frac{1}{2}$) are classical examples of Gegenbauer polynomials.

Because it inspires the development of our new Bayesian approach to spectral reprojection, we quote the main theorem in [27, Theorem 5.1]:

Theorem 1

(Removal of the Gibbs Phenomenon) Consider an analytic and non-periodic function f(x) on $[-1,1]$, satisfying

$$\begin{aligned} \max _{-1 \le x \le 1} \left| \frac{d^k f}{dx^k} (x) \right| \le C(\rho ) \frac{k!}{\rho ^k}, \qquad \rho \ge 1. \end{aligned}$$

(2.14)

Assume that the first N Fourier coefficients in (2.2) are known. Let ${\widehat{g}}^\lambda _l$, $0 \le l \le m$, be the Gegenbauer reprojection coefficients in (2.9)

$$\begin{aligned} {\widehat{g}}^\lambda _l= & \frac{1}{h_l^\lambda } \int _{-1}^{1}(1-x^2)^{\lambda -\frac{1}{2}}\,S_Nf(x)\,C^\lambda _l(x)dx \nonumber \\= & \delta _{0l} {\widehat{f}}_0 + \varGamma (\lambda ) i^l (l+\lambda ) \sum _{k = -\frac{N}{2}, k \ne 0}^{\frac{N}{2}-1} J_{l+\lambda }(\pi k) \left( \frac{2}{\pi k} \right) ^\lambda {\widehat{f}}_k, \end{aligned}$$

(2.15)

where $S_Nf$ is the Fourier partial sum given by (2.3), $\delta _{0l}$ is the Kronecker delta function, $\varGamma (\lambda )$ denotes the usual gamma function, and $J_{l+\lambda }(\pi k)$ is the Bessel function of the first kind.³ Then, for $\lambda = m =\kappa N$ where $\kappa < \frac{\pi e}{27}$, we have

$$\begin{aligned} \max _{-1 \le x \le 1} \left| f(x) - \sum _{l=0}^{m} {\widehat{g}}^\lambda _l C^{\lambda }_l(x) \right| \le A_D N^2 q_D^N + A_R q_R^N, \end{aligned}$$

(2.16)

where

$$\begin{aligned} q_D = \left( \frac{27 \kappa }{\pi e} \right) ^{\kappa }, \qquad q_R = \left( \frac{27 }{32 \rho } \right) ^{\kappa }. \end{aligned}$$

The proof found in [26, 27] makes use of the explicit form in (2.15) and follows the triangular inequality

$$\begin{aligned} \max _{-1 \le x \le 1} \left| f(x) - \sum _{l=0}^{m} {\widehat{g}}^\lambda _l C^{\lambda }_l(x) \right|\le & \max _{-1 \le x \le 1} \left| \sum _{l=0}^{m} {\widehat{f}}^\lambda _l C^{\lambda }_l(x) -\sum _{l=0}^{m} {\widehat{g}}^\lambda _l C^{\lambda }_l(x) \right| \nonumber \\ & +\max _{-1 \le x \le 1} \left| f(x) - \sum _{l=0}^{m} {\widehat{f}}^\lambda _l C^{\lambda }_l(x) \right| \nonumber \\= & ||E_{D}||_\infty + ||E_{R}||_\infty \nonumber \\\le & A_D N^2q_D^N + A_Rq_R^N. \end{aligned}$$

(2.17)

The first term, called the truncation error in [26, 27], is a measure of how well the projected data fits the true data (hence we refer to this term as the data error and use $E_D$) in the Gibbs complementary basis (here the Gegenbauer polynomials with $\lambda = \kappa N$). The regularization error ($E_R$) measures how accurate the mth-degree approximation is in the Gibbs complementary basis given the true coefficients $\{{\widehat{f}}^\lambda _l\}_{l = 0}^m$. Importantly, the error bound is provided in the maximum norm, proving that the spectral reprojection method in (2.9) using the Gegenbauer polynomials as the reprojection basis with appropriate $\lambda$ and m truly resolves the Gibbs phenomenon. We also note that referring to the two error components as respectively the data and regularization errors provides some intuition for the Bayesian approach we adopt in Sect. 4.

To summarize, given the first N Fourier coefficients (2.2) of a non-periodic analytic function on $[-1,1]$, Theorem 1 says that the Gegenbauer polynomials can be used as the Gibbs complementary basis in (2.9), with coefficients $\{\widehat{g}_l^\lambda \}_{l = 0}^m$ defined in (2.15). This yields the celebrated Gegenbauer reconstruction method

$$\begin{aligned} f_{m,N}^{\lambda }(x):= P_m^\lambda S_N f(x) = \sum _{l=0}^{m} \widehat{g}^{\lambda }_{l}\, C^\lambda _l(x), \end{aligned}$$

(2.18)

which converges exponentially to f for any $x \in [-1,1]$ in the maximum norm.

Remark 2.1

Theorem 1 does not suggest that $m = \lambda$, only that they both grow linearly with N. Indeed, while the regularization error $E_R$ decreases with larger m, the data error $E_D$ increases. Larger $\lambda$ decreases $E_D$, but creates a narrower weight function, causing the approximation to be more extrapolatory. A more thorough investigation for optimizing these parameters, based on the underlying regularity of f, can be found in [18]. Moreover, the theorem rules out using Legendre ($\lambda = \frac{1}{2}$) or Chebyshev polynomials ($\lambda = 0$), since $\lambda$ must grow linearly with N to ensure small $E_D$. Thus we see that although they both yield exponentially convergent approximations for $E_R$ according to (2.8), they do not qualify as admissible Gibbs complementary bases. Finally, it is important to note that Theorem 1 does not account for the additive Gaussian noise in (2.1), and while the general estimate still holds [5], parameter optimization is less clear. This will be further discussed in Remark 4.3, Remark 4.4, and subsection 6.2.

Although (2.18) can approximate f at any point location x in $[-1,1]$, for simplicity in this investigation we discretize the spatial domain uniformly using the same number of points as given Fourier data, so that

$$\begin{aligned} x_j = -1 + \frac{2(j-1)}{N}, \qquad j= 1,\ldots , N. \end{aligned}$$

(2.19)

Uniform discretization is also desirable as it is standard for pixelated images. We then seek to recover an approximation to the vectorized solution ${\textbf{f}}\in {\mathbb {R}}^N$, where each component of ${\textbf{f}}$ is given by $f_j = f(x_j)$, $j = 1,\dots , N$. Algorithm 1 describes how to approximate f at the prescribed gridpoints (2.19) satisfying the conditions in (2.14) given its noisy Fourier coefficients (2.1) using the blueprint provided by Theorem 1. Results for the noiseless case first described in [27] are displayed in Fig. 2.

3 Model Discretization

Since we will be formulating our problem as a discrete linear inverse problem, we now describe how the results in Sect. 2 can be discretized and expressed using matrix–vector notation. Following standard terminology for recovery problems, we will refer to ${{\textbf{f}}} = \{f(x_j)\}_{j= 1}^N \in {\mathbb {R}}^N$ as the underlying signal of interest.

Recall that for uniform grid points (2.19), the composite trapezoidal rule can be used to approximate $\widehat{{\textbf{f}}} = \{\widehat{f}_k\}_{k = -\frac{N}{2}}^{\frac{N}{2}-1}$ in (2.2) as

$$\begin{aligned} \widetilde{f}_k = \frac{1}{N}\sum _{j = 1}^N f(x_j) e^{-ik\pi x_j}, \quad -\frac{N}{2} \le k \le \frac{N}{2} -1, \end{aligned}$$

(3.1)

which we write in matrix–vector form as

$$\begin{aligned} \widetilde{{\textbf{f}}} = {\textbf{F}}{\textbf{f}}. \end{aligned}$$

(3.2)

Here $\widetilde{{\textbf{f}}} = \{\widetilde{f}_k\}_{k = -\frac{N}{2}}^{\frac{N}{2}-1}\in {\mathbb {C}}^N$, and ${\textbf{F}}\in {\mathbb {C}}^{N \times N}$ is the discrete Fourier transform (DFT) matrix with entries

$$\begin{aligned} {\textbf{F}}(n,j) = \frac{1}{N} e^{-i(n - \frac{N}{2} -1) \pi x_j}, \quad 1\le n,j \le N. \end{aligned}$$

Analogously, given Fourier coefficients $\widehat{{\textbf{f}}}= \{\widehat{f}_k\}_{k = -\frac{N}{2}}^{\frac{N}{2} -1} \in {\mathbb {C}}^N$ in (2.2), we write the corresponding discrete Fourier partial sum for (2.3) as

$$\begin{aligned} {\textbf{f}}_N = \widehat{{\textbf{F}}}^{*} \,\widehat{{\textbf{f}}}, \end{aligned}$$

(3.3)

where $\widehat{{\textbf{F}}}^{*} \in {\mathbb {C}}^{N \times N}$ is the (un-normalized) complex conjugate transpose of ${\textbf{F}}$ in (3.2), also referred to as the discrete inverse Fourier transform operator with entries⁴

$$\begin{aligned} \widehat{{\textbf{F}}}^{*}(j,n) = e^{i (n-\frac{N}{2}-1) \pi x_j}, \quad \quad 1\le j,n \le N. \end{aligned}$$

Observe that ${\textbf{f}}_N = \{S_N f(x_j)\}_{j = 1}^N \in {\mathbb {R}}^N$ due to cancellation of the imaginary terms.

Remark 3.1

Due to aliasing, (3.2) is not equivalent to (2.2), with the explicit relationship given by (see e.g. [29])

$$\begin{aligned} \widetilde{f}_k = \widehat{f}_k + \sum _{\begin{array}{c} |q| \le \infty \\ q \ne 0 \end{array}}{\hat{f}}_{k + \frac{Nq}{2}}, \quad -\frac{N}{2} \le k \le \frac{N}{2} -1, \end{aligned}$$

which we will write simply as

$$\begin{aligned} \widehat{{\textbf{f}}} = \widetilde{{\textbf{f}}} + {\varvec{\delta }}_{f} = {\textbf{F}}{\textbf{f}}+ {\varvec{\delta }}_{f}, \end{aligned}$$

(3.4)

with ${\varvec{\delta }}_{f} \in {\mathbb {C}}^N$ representing the aliasing error. It is typically assumed that the magnitude components of ${\varvec{\delta }}_{f}$ are smaller than those in $\widehat{\varvec{\epsilon }} = \{\epsilon _k\}_{k = -\frac{N}{2}}^{\frac{N}{2}-1}$ defined in (2.1), and therefore the model discrepancy is reasonable (see e.g. [6]). Indeed, the traditional observation data model corresponding to (2.1) follows (3.4) and is defined as

$$\begin{aligned} \widehat{{\textbf{b}}} = {\textbf{F}}{\textbf{f}}+ \widetilde{{\varvec{\epsilon }}}, \end{aligned}$$

(3.5)

where by construction $\widetilde{{\varvec{\epsilon }}} = \widehat{{\varvec{\epsilon }}} + {\varvec{\delta }}_{f} \in {\mathbb {C}}^N$ follows a circularly-symmetric complex normal distribution. We will use (3.5) in Sect. 5 and further characterize the noise distribution there.

Remark 3.2

For simplicity we also use the same notation in (3.3) for the discretized Fourier partial sum given noisy Fourier coefficients $\widehat{{\textbf{b}}}= \{\widehat{b}_k\}_{k = -\frac{N}{2}}^{\frac{N}{2} -1} \in {\mathbb {C}}^N$ in (2.1). That is, we write

$$\begin{aligned} {\textbf{f}}_N = \widehat{{\textbf{F}}}^{*} \,\widehat{{\textbf{b}}}. \end{aligned}$$

(3.6)

Which of (3.3) or (3.6) is employed will be contextually evident.

The corresponding discrete Gegenbauer partial sum (2.12) can be written as

$$\begin{aligned} {\textbf{f}}_m^\lambda = {\textbf{F}}^{Geg} \,\widehat{{\textbf{f}}}^{\lambda }, \end{aligned}$$

(3.7)

where ${\textbf{f}}_{m}^{\lambda }=\{P_{m}^{\lambda } f(x_j)\}_{j = 1}^{N} \in {\mathbb {R}}^N$ and $\widehat{{\textbf{f}}}^{\lambda }= \{\widehat{f}^{\lambda }_{l}\}_{l = 0}^m \in {\mathbb {R}}^{m+1}$. Here ${\textbf{F}}^{Geg} \in {\mathbb {R}}^{N \times (m+1)}$ with entries

$$\begin{aligned} {\textbf{F}}^{Geg}(j,n) = C_{n-1}^{\lambda }(x_j), \quad \quad 1\le j\le N, \quad \quad 1 \le n \le m+1. \end{aligned}$$

(3.8)

Since the Gegenbauer coefficients $\widehat{{\textbf{f}}}^{\lambda }$ in (2.13) are not explicitly known for our problem, we use the composite trapezoidal rule to obtain the approximation

$$\begin{aligned} \widetilde{f}^{\lambda }_{l} = \frac{1}{h^\lambda _l} \cdot \frac{2}{N} \sum _{j=1}^{N} (1-x_j^2)^{\lambda -\frac{1}{2}} f(x_j) C^\lambda _l(x_j),\quad \quad l = 0,\dots ,m, \end{aligned}$$

(3.9)

as the components of $\widetilde{{\textbf{f}}}^{\lambda } \in {\mathbb {R}}^{m+1}$, noting that the integrand evaluation vanishes at both boundaries for $\lambda > \frac{1}{2}$ and that the smoothness of the integrand increases with $\lambda$. Combining (3.8) and (3.9) yields

$$\begin{aligned} \widetilde{{\textbf{f}}}^{\lambda } = {\textbf{F}}^{CT} \,{\textbf{f}},\quad \displaystyle {\textbf{F}}^{CT}=\frac{2}{N}{\textbf{H}}\left( {\textbf{F}}^{Geg} \right) ^T {\textbf{W}}. \end{aligned}$$

(3.10)

Here ${\textbf{H}}\in {\mathbb {R}}^{(m+1)\times (m+1)}$ is the diagonal normalizing matrix with entries ${\textbf{H}}(l,l) =\frac{1}{h^\lambda _l}$ and ${\textbf{W}}\in {\mathbb {R}}^{N \times N}$ is the diagonal weighting matrix with entries ${\textbf{W}}(j,j) = (1-x_j^2)^{\lambda -\frac{1}{2}}$.

Related to the discussion in Remark 3.1, there is a quadrature error associated with the Gegenbauer coefficients which we simply write as

$$\begin{aligned} \widehat{{\textbf{f}}}^{\lambda } = \widetilde{{\textbf{f}}}^{\lambda } + {\varvec{\delta }}_{g} = {\textbf{F}}^{CT} \, {\textbf{f}}+ {\varvec{\delta }}_{g}, \end{aligned}$$

(3.11)

so that the corresponding model for (3.7) is

$$\begin{aligned} {\textbf{f}}_m^\lambda = {\textbf{F}}^{Geg}\widetilde{{\textbf{f}}}^\lambda + {\textbf{F}}^{Geg}{\varvec{\delta }}_g = {\textbf{F}}^{Geg}{\textbf{F}}^{CT}{\textbf{f}}+ \widetilde{{\varvec{\delta }}}_g, \end{aligned}$$

(3.12)

where $\widetilde{{\varvec{\delta }}}_g = {\textbf{F}}^{Geg}{\varvec{\delta }}_g$ can be considered as noise resulting from not having the exact Gegenbauer coefficients $\widehat{{\textbf{f}}}^\lambda$. Moreover, assuming large enough N, the error ${\varvec{\delta }}_g$ incurred using (3.9) is typically smaller than the overall error in the approximation due to the additive noise in (2.1). A couple of remarks are in order.

Remark 3.3

The accuracy of the quadrature formula (3.9) is inherently dependent on the properties of f(x) and the choice of $\lambda$, which is slightly more nuanced. On the one hand, larger $\lambda$ makes the corresponding integrand smoother, meaning that the trapezoidal rule yields greater accuracy. On the other hand, constructing $(1-x^2)^{\lambda - \frac{1}{2}}$ for larger $\lambda$ requires more resolution. We make the assumption that there are enough Fourier coefficients (N) to resolve the underlying function using Gegenbauer reconstruction, i.e., the problem in the continuous case is not under-determined when using (2.15). This choice of N for the quadrature informs (3.11).

Remark 3.4

We note that it is possible to get increased accuracy for (3.11), for example, by approximation with Chebyshev Gauss quadrature on the Chebyshev Gauss quadrature points. While it is straightforward to derive the matrix form for (3.11), due to the set up for the inverse problem, the forward operator ${\textbf{F}}$ will need to be changed as the signal needs to be recovered at different points. In this case, the discrete Fourier transform matrix ${\textbf{F}}$ can no longer be used, which in addition to being less computationally efficient, also introduces another error term to account for in the data fidelity term. In this sense, there is a trade-off between the accuracy of the likelihood and prior term. Either will be typically smaller than the overall error due to the additive noise for our choice of SNR, thus for simplicity, we keep the current setup.

Finally, we provide the discretized model for spectral reprojection in (2.21). This is accomplished by first defining $\widehat{{\textbf{g}}}^{\lambda }= \{\widehat{g}^{\lambda }_{l}\}_{l = 0}^m$, with each component $\widehat{g}^\lambda _l$ given by (2.20), which we write as

$$\begin{aligned} \widehat{{\textbf{g}}}^{\lambda } = {\textbf{F}}^{Bessel} \,\widehat{{\textbf{b}}}. \end{aligned}$$

(3.13)

Here ${\textbf{F}}^{Bessel} \in {\mathbb {C}}^{(m+1) \times N}$ has entries

$$\begin{aligned} {\textbf{F}}^{Bessel}(j,n) = {\left\{ \begin{array}{ll} 1, \hspace{5cm} \text{ if }\ j = 1\ \text{ and }\ n=\frac{N}{2}+1, \\ 0, \hspace{5cm} \text{ if }\ j > 1\ \text{ and }\ n=\frac{N}{2}+1, \\ \displaystyle \varGamma (\lambda ) i^{j-1}(j-1+\lambda ) J_{j-1+\lambda }(\pi k) \left( \frac{2}{\pi k}\right) ^{\lambda }, \qquad \text{ otherwise }, \end{array}\right. } \end{aligned}$$

(3.14)

for $1\le j \le m+1$, $1 \le n \le N$ and $k = n - \frac{N}{2} - 1$.

By defining ${\textbf{f}}_{m,N}^{\lambda }= \{f_{m,N}^{\lambda }(x_j)\}_{j = 1}^N$, we have the discretized formulation of (2.21):

$$\begin{aligned} {\textbf{f}}_{m,N}^\lambda = {\textbf{F}}^{Geg} \,\widehat{{\textbf{g}}}^{\lambda } = {\textbf{F}}^{Geg} {\textbf{F}}^{Bessel}\widehat{{\textbf{b}}}. \end{aligned}$$

(3.15)

Note that (3.15) is directly obtained from the given measurements $\widehat{{\textbf{b}}}$ in (2.1), that is, there is no additional model error (noise) incurred by implementation. Therefore, when comparing (3.15) to (3.12), we obtain the observation model

$$\begin{aligned} {\textbf{f}}_{m,N}^\lambda = {\textbf{f}}_m^\lambda + {\varvec{\epsilon }}^\lambda = {\textbf{F}}^{Geg}{\textbf{F}}^{CT}{\textbf{f}}+ {\varvec{\epsilon }}^\lambda , \end{aligned}$$

(3.16)

where the additive noise ${\varvec{\epsilon }}^\lambda$ has contributions both from $\widehat{\varvec{\epsilon }}$ in (2.1) and $\widetilde{\varvec{\delta }}_g$ in (3.12).

4 A Bayesian Framework for Spectral Reprojection

Spectral reprojection has been successfully used to recover non-periodic (or piecewise smooth) functions from Fourier data in a variety of contexts, including post-processing solutions for numerical conservation laws [29] and recovering images for segmentation purposes [3]. Although some noise is always present, either in the form of numerical simulation error or data acquisition error, most studies have not formally analyzed its contribution to the overall error. However, in [5] it was shown that while the Gegenbauer approximation is an unbiased estimator for additive Gaussian noise, the variance depends on the particular approximation location, with increased variance near the boundaries (or edge locations of piecewise smooth functions). Filtering can reduce the overall variance, but requires further tuning, and moreover leads to a loss of resolution. These issues motivate us to gain a better understanding of the spectral reprojection method using a statistical framework, as we now describe.

We first note that the proof of Theorem 1, and specifically the triangular inequality (2.17), provides a blueprint for formulating a Bayesian approach. In particular the inequality also holds for $\Vert \cdot \Vert _2$ up to a constant.⁵ Second, the data error term $E_D$ in (2.17) is analogous to the likelihood term in a maximum a posterior (MAP) estimate for a posterior distribution of the unknown signal ${{\textbf{f}}}$ in the discretized framework. Finally, the regularization error term $E_{R}$ in (2.17) measures the difference between the function and its Gegenbauer partial sum approximation (2.12), which can be viewed as our prior belief about ${\textbf{f}}$. That is, we expect the signal ${\textbf{f}}$ to be close to ${\textbf{f}}_m^\lambda$ in (3.12). In a nutshell, these insights allow us to view spectral reprojection from a Bayesian perspective for fixed values of m and $\lambda$. We will refer to this approach as the Bayesian Spectral Reprojection (BSR) method.

Remark 4.1

As our numerical experiments will show in Sect. 6, the Bayesian spectral reprojection method yields estimates that are similar to those determined from Algorithm 1, which is to be expected based on its design. An advantage to our new Bayesian formulation is that unlike other traditionally chosen priors (e.g. sparse priors), its derivation is motivated by rigorous error approximation analysis. Moreover, as we will describe below, it is also possible to partially quantify the uncertainty of the underlying approximation.

4.1 Statistical Formulation for Spectral Reprojection

Inspired by the spectral reprojection method as discretized by (3.12) and (3.15), we now seek a statistical formulation for the recovery of the unknown signal ${\textbf{f}}$. We begin by considering the linear inverse problem

$$\begin{aligned} {{\mathcal {G}}}={{\mathcal {A}}}{\mathcal {X}}+{{\mathcal {E}}}, \end{aligned}$$

(4.1)

where ${\mathcal {X}}$, ${{\mathcal {G}}}$, and ${{\mathcal {E}}}$ are random variables defined over a common probability space, and ${\mathcal {X}}$ and ${{\mathcal {E}}}$ are assumed to be independent. In this framework ${\mathcal {X}}$ represents the unknown which we seek to recover, ${{\mathcal {G}}}$ denotes the observables, ${{\mathcal {A}}}$ is a known linear operator, and ${{\mathcal {E}}}\sim {\mathcal {N}}({{\textbf{0}}},\gamma ^{-1} {\textbf{I}}_N)$ is a vector of independent and identically distributed (i.i.d.) Gaussian noise with mean 0 and unknown variance $\gamma ^{-1}$. Finally throughout this manuscript we use ${\textbf{I}}_N$ to denote the $N\times N$ identity matrix.

Remark 4.2

As already noted, the variance of the Gegenbauer approximation has non-trivial expression and depends on the particular approximation location [5]. The assumption about the covariance matrix of ${\mathcal {E}}$ being a constant multiple of the identity matrix therefore generally does not hold. We nevertheless adopt it for simplicity in (4.1). A more refined error distribution characterization may be obtained via sampling methods, although this would require significant computational effort.

With (3.16) representing the observational model system, the realizations of each random variable in (4.1) respectively are the unknown vector of interest ${\textbf{f}}\in {\mathbb {R}}^N$, the observable data ${\textbf{f}}_{m,N}^\lambda \in {\mathbb {R}}^N$ in (3.15), and noise vector ${\varvec{\epsilon }}^\lambda \in {\mathbb {R}}^N$. A hierarchical Bayesian model based on Bayes’ theorem then provides an estimate of the full posterior distribution given by

$$\begin{aligned} p_{{\mathcal {X}}, {\varTheta } \,| \,{{\mathcal {G}}}}({\textbf{f}},{\varvec{\theta }} \,|\,{\textbf{f}}_{m,N}^\lambda ) \propto p_{{{\mathcal {G}}}\,|\,{\mathcal {X}},{\varTheta }}({\textbf{f}}_{m,N}^\lambda \, | \,{\textbf{f}},{\varvec{\theta }}) \, p_{{\mathcal {X}}\,| \,{\varTheta }}({\textbf{f}}\,| \,{\varvec{\theta }}) \, p_{{\varTheta }}({\varvec{\theta }}), \end{aligned}$$

(4.2)

where $p_{{{\mathcal {G}}}\,|\,{\mathcal {X}},{\varTheta }}({\textbf{f}}_{m,N}^\lambda \, | \,{\textbf{f}},{\varvec{\theta }})$ is the likelihood density function determined by relationship between ${\textbf{f}}$ and ${\textbf{f}}_{m,N}^\lambda$ and assumptions on ${{\mathcal {E}}}$, $p_{{\mathcal {X}}\,| \,{\varTheta }}({\textbf{f}}\,| \,{\varvec{\theta }})$ is the density of the prior distribution encoding a priori assumptions about the solution, and $p_{{\varTheta }}({\varvec{\theta }})$ is the hyperprior density for all other involved parameters, which we denote collectively as ${\varvec{\theta }}$. In our investigation $p_{{\varTheta }}({\varvec{\theta }}) = p_\upgamma (\gamma ) \,p_\upbeta (\beta )$, where $\gamma$, $\beta$ corresponds to the inverse noise and inverse prior variances respectively (see subsection 4.4). Note that the right hand side of (4.2) is not normalized (hence $\propto$ is used), but as the normalized version is often not computationally tractable, it is the posterior typically sought in Bayesian inference methods. In what follows we describe how to construct the corresponding likelihood, prior and hyperprior density functions.

4.2 Formulating the Likelihood

The likelihood density function $p({\textbf{f}}_{m,N}^\lambda \,| \,{\textbf{f}}, \gamma )$ in (4.2) models the connection between the signal and observation vectors.⁶ As already noted, the data error term $E_D$ in (2.17) states intuitively that ${\textbf{f}}_{m,N}^{\lambda }$ is close to ${\textbf{f}}_m^\lambda$, while ${\textbf{f}}_m^\lambda$ is related to the underlying signal ${\textbf{f}}$ via (3.12). This insight allows us to define the observation model as (3.16), and more specifically to prescribe the distribution for the likelihood as

$$\begin{aligned} {\textbf{f}}_{m,N}^{\lambda } \sim {\mathcal {N}}({\textbf{F}}^{Geg}{\textbf{F}}^{CT} {\textbf{f}}, \gamma ^{-1}{\textbf{I}}), \end{aligned}$$

(4.3)

with the interpretation that the data error ${{{\varvec{\epsilon }}}^\lambda } = {\textbf{f}}_{m,N}^{\lambda } - {\textbf{F}}^{Geg}{\textbf{F}}^{CT} {\textbf{f}}$ corresponding to $E_D$ follows the distribution ${\mathcal {N}}({{\textbf{0}}},\gamma ^{-1} {\textbf{I}}_N)$ for unknown variance $\gamma ^{-1}$. Thus

$$\begin{aligned} p({{\varvec{\epsilon }}}^\lambda \,| \, \gamma )= \left( \frac{\gamma }{2\pi }\right) ^{\frac{N}{2}}\exp \left( -\frac{\gamma }{2} \Vert {{\varvec{\epsilon }}}^\lambda \Vert _2^2 \right) . \end{aligned}$$

(4.4)

The likelihood density function is determined entirely from (4.4), yielding

$$\begin{aligned} p({\textbf{f}}_{m,N}^\lambda \,|\,{\textbf{f}},\gamma ) = \left( \frac{\gamma }{2\pi }\right) ^{\frac{N}{2}}\exp (-\frac{\gamma }{2} \Vert {\textbf{f}}_{m,N}^\lambda - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}\, {\textbf{f}}\Vert _2^2). \end{aligned}$$

(4.5)

Importantly, we observe that ${\textbf{f}}_{m,N}^{\lambda } = {\textbf{F}}^{Geg} {\textbf{F}}^{Bessel}\widehat{{\textbf{b}}}$ is obtained directly by linear transformation of the measurement data $\widehat{{\textbf{b}}}$ via (3.15).

4.3 Formulating the Prior

The prior function models our prior belief about the unknown signal ${\textbf{f}}$. In this investigation ${\textbf{f}}= \{f(x_j)\}_{j = 1}^N$ where f is analytic in $[-1,1]$, and hence, due to (2.8), a distribution for the true solution ${\textbf{f}}$ can be motivated using (3.12), resulting in

$$\begin{aligned} {\mathcal {X}}\sim {\mathcal {N}}({{\textbf{f}}}^{\lambda }_{m}, \beta ^{-1} {\textbf{I}}_{N} ), \end{aligned}$$

(4.6)

where ${{\textbf{f}}}^{\lambda }_{m}$ is the Gegenbauer partial sum approximation in (3.12) with a hyperprior $\beta >0$ being inverse variance. Essentially, since the regularization error term $E_{R}$ measures the difference between the function and its approximation with Gegenbauer basis, we expect the signal ${\textbf{f}}$ to be close to ${\textbf{f}}^{\lambda }_{m}$, leading to the conditionally Gaussian prior function

$$\begin{aligned} p({\textbf{f}}\,| \,\beta ) = \left( \frac{\beta }{2\pi }\right) ^{\frac{N}{2}}\exp \left( -\frac{\beta }{2}\Vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}){\textbf{f}}\Vert _2^2 \right) . \end{aligned}$$

(4.7)

A few remarks are in order:

Remark 4.3

(Choice of $\lambda$) Our choice for $\lambda$ is motivated by Theorem 1, even though our underlying assumption about f being analytic in $[-1,1]$ means that it can be approximated equally well by any orthogonal polynomial expansion (2.4), that is for all $\lambda \ge 0$ coinciding with $w_\lambda (x) = (1-x^2)^{\lambda - \frac{1}{2}}$. In particular Chebyshev ($\lambda =0$) and Legendre ($\lambda =\frac{1}{2})$ polynomials would be appropriate choices in this case. For the trapezoidal rule to be accurate using equally spaced nodes ((3.9) and later (4.7)) a sufficient number of vanishing derivatives of the integrand function at $\pm 1$ is needed, further motivating the use of “large enough” $\lambda$. By contrast, it was demonstrated in [11] that if $\lambda$ is too large, the Gegenbauer reprojection method yields poor results, mainly due to the narrow region of support of $w_\lambda (x)$ (Definition 2.1). To this end we note that other Gibbs complementary bases, such as the Freud polynomials used in [20], are more robust. The benefits in this case are only realized when N is very large, a consequence of the resolution requirements for the corresponding polynomial approximation. As it is important in the context of inverse problems that the solution be obtainable without a large number of measurements, we restrict our study to Gegenbauer polynomials. Our specific choices for $\lambda$, especially as a function of SNR, is discussed in more detail in Sect. 6.3.

Remark 4.4

(Choice of m) We also choose m to satisfy Theorem Theorem 1, which follows from (2.8). Although it is possible to make both $\lambda$ and m unknown random variables, this will greatly increase the computational cost owing to the computation of ${\textbf{F}}^{Geg}$ and ${\textbf{F}}^{CT}$ which would no longer be deterministic. In particular the dimensions of ${\textbf{F}}^{Geg}$ would change for each iteration. Since our prior pertains to the analyticity of the underlying function f, adopting m according to (2.8) is reasonable.

Remark 4.5

(Sparse priors) Priors are often constructed to satisfy the assumption that the underlying solution is sparse in some transform domain, such as the gradient or wavelet domain, see e.g. [15, 23, 28, 31] and references therein. From this perspective, since the decay of the orthogonal polynomial coefficients for f is exponential, we could construct a sparse prior where the transform domain is computed in (3.10) for $\lambda \ge 0$. The resulting prior would be similar to those used in the above references with the notable exception that for $m \sim \kappa N$ satisfying Theorem 1, we are allowing the underlying function to have considerable variability, which is much less restrictive than using the gradient or low-order wavelet transforms. Since our goal is to express spectral reprojection in a Bayesian framework, we do not compare our new method to formulations using sparse priors in this investigation.

4.4 Formulating the Hyperpriors

In (4.2) we denoted $p({\varvec{\theta }})$ as the hyperprior density function for any additional parameters needed to describe the hierarchical model. As noted there, this amounts to $p({\varvec{\theta }}) = p(\gamma )\, p(\beta )$, with $\gamma , \beta$ being the inverse noise variance and inverse prior variance respectively. Choosing $\gamma$ and $\beta$ to be Gamma distributions is convenient since their corresponding densities are conjugate for their respective conditional Gaussian distributions (4.5) and (4.7). In particular, the resulting product distribution is a conditional Gaussian distribution, with mean and covariance known explicitly, see e.g. [15, 23].

The Gamma distribution has probability density function

$$\begin{aligned} \varGamma ( \eta \,|\, c,d ) = \frac{d^c}{\varGamma (c)} \eta ^{c-1} e^{-d\eta }, \end{aligned}$$

(4.8)

where c and d are positive shape and rate parameters. For $c \rightarrow 1$ and $d \rightarrow 0$, (4.8) is an uninformative prior, which is desirable since we do not want these parameters to have undue influence on the solution. Thus here for simplicity we choose

$$\begin{aligned} & p(\gamma )= \varGamma (\gamma \, \vert \, c, d), \end{aligned}$$

(4.9a)

$$\begin{aligned} & p(\beta )= \varGamma (\beta \, \vert \, c, d). \end{aligned}$$

(4.9b)

with $c=1$ and $d=10^{-4}$ for all of our numerical examples. Following the above discussion, we then replace $p({\varvec{\theta }})$ in (4.2) with

$$\begin{aligned} p({\varvec{\theta }}) = p(\gamma )p(\beta ) \propto \gamma ^{c-1} \exp (-d \, \gamma ) \, \beta ^{c-1} \exp (-d \, \beta ). \end{aligned}$$

(4.10)

4.5 Bayesian Inference

We now have all of the ingredients needed to construct (4.2). Specifically, substituting in the likelihood (4.5), the prior (4.7) and the hyperprior (4.10) density functions into (4.2), we obtain the posterior density function approximation

$$\begin{aligned} p({\textbf{f}}, \gamma , \beta \, \vert \, {\textbf{f}}_{m,N}^\lambda )\propto & \gamma ^ {c+\frac{N}{2}-1} \beta ^{c+\frac{N}{2} -1} \exp \bigg \{ -\frac{\gamma }{2} \Vert {\textbf{f}}_{m,N}^\lambda - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}\, {\textbf{f}}\Vert _2^2 \nonumber \\ & -\frac{\beta }{2} \Vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}){\textbf{f}}\Vert _2^2 -d \, \gamma -d \, \beta \bigg \}. \end{aligned}$$

(4.11)

From here we can obtain the MAP estimate, which is equivalent to minimizing the negative logarithm of the right hand side of (4.11), yielding the objective function

$$\begin{aligned} {{\mathcal {J}}}({\textbf{f}}, \gamma , \beta )= & -(c+\frac{N}{2}-1) \log (\gamma ) -(c+\frac{N}{2}-1) \log (\beta ) \nonumber \\ & + \frac{\gamma }{2} \Vert {\textbf{f}}_{m,N}^\lambda - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}\, {\textbf{f}}\Vert _2^2 + \frac{\beta }{2} \Vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) {\textbf{f}}\Vert _2^2 +d \, \gamma +d \,\beta \nonumber \\ \end{aligned}$$

(4.12)

up to a constant that is independent of ${\textbf{f}}$, $\gamma$, and $\beta$. In what follows we discuss how to minimize (4.12).

4.5.1 The Block-Coordinate Descent Approach

We use a block-coordinate descent (BCD) approach [8, 44] to approximate the MAP estimate of (4.11). In particular, BCD minimizes ${\mathcal {J}}$ in (4.12) by alternating minimization w.r.t. ${\textbf{f}}$ for fixed $\gamma , \beta$, minimization w.r.t. $\gamma$ for fixed ${\textbf{f}},\beta$, and minimization w.r.t. $\beta$ for fixed ${\textbf{f}},\gamma$. That is, given an initial guess for the hyperparameters $\gamma$ and $\beta$, the BCD algorithm proceeds through a sequence of updates of the form

$$\begin{aligned} & {\textbf{f}}= \underset{{\textbf{f}}}{\text {arg min}} \left\{ {{\mathcal {J}}}({\textbf{f}},\gamma , \beta ) \right\} , \end{aligned}$$

(4.13a)

$$\begin{aligned} & \gamma = \underset{\gamma }{\text {arg min}} \left\{ {{\mathcal {J}}}({\textbf{f}},\gamma , \beta ) \right\} , \end{aligned}$$

(4.13b)

$$\begin{aligned} & \beta = \underset{\beta }{\text {arg min}} \left\{ {{\mathcal {J}}}({\textbf{f}},\gamma , \beta ) \right\} , \end{aligned}$$

(4.13c)

until a convergence criterion is met. In our implementation we initialize the hyperparameter vectors as $\gamma = 1$ and $\beta = 1$, and we stop when either the relative change of the objective function value or the relative change in ${\textbf{f}}$ falls below a given threshold. Efficient implementation of the three update steps in (4.13) is described below.

4.5.2 Updating the Unknown Signal ${\textbf{f}}$

Due to our intentionally chosen conditionally Gaussian prior (4.7) and Gamma hyperprior (4.9a)–(4.9b), for fixed $\gamma$ and $\beta$ we have

$$\begin{aligned} p({\textbf{f}}\,|\, {\textbf{f}}_{m,N}^\lambda , \gamma , \beta ) \propto p({\textbf{f}}_{m,N}^\lambda \, | \, {\textbf{f}}, \gamma ) \, p({\textbf{f}}\, | \, \beta ) \propto {\mathcal {N}}({\varvec{\mu }}, C), \end{aligned}$$

(4.14)

where the mean ${\varvec{\mu }}$ and the covariance matrix C are respectively given by [22, 23]

$$\begin{aligned} {\varvec{\mu }}= \gamma \, C ({{\textbf{F}}^{Geg} {\textbf{F}}^{CT}})^{T} \, {\textbf{f}}_{m,N}^\lambda \end{aligned}$$

(4.15)

and

$$\begin{aligned} C = \left( \gamma \, ({{\textbf{F}}^{Geg} {\textbf{F}}^{CT}})^{T} ({{\textbf{F}}^{Geg} {\textbf{F}}^{CT}}) + \beta \,({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) ^ T ({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT})\right) ^{-1}. \end{aligned}$$

(4.16)

Since the mean and MAP estimate are equivalent for Gaussian distributions, the update step for ${\textbf{f}}$ in (4.13a) reduces to solving (4.15), yielding the system

$$\begin{aligned} & \left( \gamma \, ({{\textbf{F}}^{Geg} {\textbf{F}}^{CT}})^{T} ({{\textbf{F}}^{Geg} {\textbf{F}}^{CT}}) + \beta \,({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) ^ T ({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT})\right) {\textbf{f}}\nonumber \\ & \quad = \gamma \, ({{\textbf{F}}^{Geg} {\textbf{F}}^{CT}})^{T} \, {\textbf{f}}_{m,N}^\lambda . \end{aligned}$$

(4.17)

We also note that by construction the common kernel condition (see e.g. [32])

$$\begin{aligned} \text {kernel}( {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) \cap \text {kernel}({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) = \{ {{\textbf{0}}} \} \end{aligned}$$

(4.18)

is automatically satisfied, and hence (4.17) has a unique solution which can be directly obtained.

Remark 4.6

Recall that the kernel of an operator $G: {\mathbb {C}}^N \rightarrow {\mathbb {C}}^M$ is given by $\text {kernel}(G) = \{ \, {\textbf{f}}\in {\mathbb {C}}^N \mid G {\textbf{f}}= {{\textbf{0}}} \, \}$, that is, the set of vectors that are mapped to zero. The common kernel condition (4.18) ensures that the prior (regularization) introduces a sufficient amount of complementary information to the likelihood (the given measurements) to make the problem well-posed, which is a standard assumption in regularized inverse problems [32, 41].

Analogous to the objective function (4.12), we also note that (4.17) is equivalent to updating ${\textbf{f}}$ via the quadratic optimization problem

$$\begin{aligned} {\textbf{f}}= \underset{{\textbf{f}}}{\text {arg min}} \left\{ \frac{\gamma }{2} \Vert {\textbf{f}}_{m,N}^\lambda - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}\, {\textbf{f}}\Vert _2^2 +\frac{\beta }{2} \Vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) {\textbf{f}}\Vert _2^2 \right\} . \end{aligned}$$

(4.19)

Various methods can be used to efficiently solve (4.19), including the fast iterative shrinkage-thresholding (FISTA) algorithm [9], the preconditioned conjugate gradient (PCG) method [37], potentially combined with an early stopping based on Morozov’s discrepancy principle [12,13,14], and the gradient descent approach [23]. There is no general advantage of one method over another, and the choice should be made based on the specific problem at hand.

4.5.3 Updating the Hyperparameters ${\gamma }$ and ${\beta }$

We now address the update for the hyperparameter $\gamma$ for fixed ${\textbf{f}}$ and $\beta$. Substituting (4.12) into (4.13b) and ignoring all terms that do not depend on $\gamma$ yields

$$\begin{aligned} \gamma= & \underset{\gamma }{\text {arg min}}\left\{ {\mathcal {J}}_\gamma \right\} \nonumber \\= & \underset{\gamma }{\text {arg min}} \left\{ -(c+\frac{N}{2}-1) \log (\gamma ) + \frac{\gamma }{2} \Vert {\textbf{f}}_{m,N}^\lambda - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}\, {\textbf{f}}\Vert _2^2 +d \, \gamma \right\} . \end{aligned}$$

(4.20)

Solving $\displaystyle \frac{d{\mathcal {J}}_\gamma }{d\gamma } = 0$ then provides

$$\begin{aligned} \gamma = \frac{2c+N-2}{\Vert {\textbf{f}}_{m,N}^\lambda - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}\, {\textbf{f}}\Vert _2^2+2d} \end{aligned}$$

(4.21)

for the $\gamma$-update. The $\beta$-update is similarly obtained as

$$\begin{aligned} \beta = \frac{2c+N-2}{ \Vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) {\textbf{f}}\Vert _2^2+2d}. \end{aligned}$$

(4.22)

Algorithm 2 summarizes the iterative process for finding the point estimate solution ${\textbf{f}}$ in (4.13) along with precision values $\gamma$ and $\beta$.

Remark 4.7

(Fixed hyperparameters) We note that the posterior formulation in (4.11) allows for uncertainty quantification for the recovered solution ${\textbf{f}}$ for fixed $\gamma$ and $\beta$. Specifically, from (4.14) we have

$$\begin{aligned} p({\textbf{f}}\,|\, {\textbf{f}}_{m,N}^\lambda ) \propto p({\textbf{f}}_{m,N}^\lambda \, | \, {\textbf{f}}) \, p({\textbf{f}}) \propto {\mathcal {N}}({\varvec{\mu }}, C), \end{aligned}$$

(4.23)

where the mean ${\varvec{\mu }}$ and the covariance matrix C are again respectively given by (4.15) and (4.16). We can then sample directly from ${\mathcal {N}}({\varvec{\mu }}, C)$ to obtain credible intervals⁷ for every component of the solution ${\textbf{f}}$. When $\gamma$ and $\beta$ are themselves random variables, computational sampling is needed to recover (4.11), for instance, full posterior sampling using a Markov chain Monte Carlo (MCMC) method [35], typically requiring considerable computational expense.

5 Generalized Bayesian Spectral Reprojection

By design, and as will be demonstrated via numerical experiments in Sect. 6, the BSR method in Algorithm 2 yields comparable point estimates as the original spectral reprojection method in Algorithm 1. We are furthermore able to quantify the uncertainty of the approximation for fixed hyperparameters $\gamma$ and $\beta$ (see Remark 4.7). Several potential shortcomings of the BSR approach are readily apparent, however. Specifically, methods for computational inverse problems are designed to promote solutions that yield close approximations to the observable information while also being constrained by assumptions regarding the underlying signal. In addition to mitigating the effects of ill-posedness, the regularization (prior) term also serves to avoid over-fitting. By construction, the likelihood and prior terms in posterior density function (4.11) are both based on the assumption that $f \in {\mathbb {P}}_m^\lambda$, that is, the space of Gegenbauer polynomials given by (2.4). While such an assumption is suitable for solving the forward problem in Algorithm 1, it inherently limits the space of possible solutions when considering the inverse problem. A more natural approach for solving linear inverse problems with i.i.d. additive (complex) Gaussian noise is to directly fit the given data model in the construction of the likelihood, and then determine a suitable prior (regularization) for fitting the data model. In this regard, our insights in using the spectral reprojection prior (4.7) still remain, in particular pertaining to the discussion in Remarks 4.3 and 4.4.

Given these insights, we now introduce the generalized Bayesian spectral reprojection (GBSR) method. We demonstrate its advantages in generating the MAP estimate with regard to accuracy and robustness in our numerical experiments in Sect. 6, where we also display credible intervals for fixed hyperparameters.

5.1 Formulating the Inverse Problem

We begin by considering the linear inverse problem

$$\begin{aligned} \widehat{{\mathcal {B}}}={\mathcal {F}}{\mathcal {X}}+ \widetilde{{\mathcal {E}}}, \end{aligned}$$

(5.1)

where ${\mathcal {X}}$, $\widehat{{\mathcal {B}}}$, and $\widetilde{{\mathcal {E}}}$ are random variables defined over a common probability space, and ${\mathcal {X}}$ and $\widetilde{{\mathcal {E}}}$ are assumed to be independent. As before, ${\mathcal {X}}$ represents the unknown which we seek to recover, $\widehat{{\mathcal {B}}}$ denotes the observables, ${\mathcal {F}}$ is a known linear operator, and $\widetilde{{\mathcal {E}}}\sim {\mathcal {C}}{\mathcal {N}}({{\textbf{0}}},\widetilde{\gamma }^{-1} {\textbf{I}}_N)$ is a vector of independent and identically distributed (i.i.d.) circularly symmetric complex Gaussian noise with mean 0 and unknown variance $\widetilde{\gamma }^{-1}$.⁸ The realizations of the random variables in (5.1) are modeled in (3.5), respectively by ${\textbf{f}}\in {\mathbb {R}}^N$, $\widehat{{\textbf{b}}} \in {\mathbb {C}}^N$, and $\widetilde{{\varvec{\epsilon }}} \in {\mathbb {C}}^N$.

We now proceed to formulate the corresponding posterior density function given by

$$\begin{aligned} p({\textbf{f}},\widetilde{\varvec{\theta }} \,|\,\widehat{{\textbf{b}}}) \propto p(\widehat{{\textbf{b}}} \, | \,{\textbf{f}},\widetilde{\varvec{\theta }}) \, p({\textbf{f}}\,| \,\widetilde{\varvec{\theta }}) \, p(\widetilde{\varvec{\theta }}), \end{aligned}$$

(5.2)

where, analogously to (4.2), $p(\widehat{{\textbf{b}}} \,| \,{\textbf{f}},\widetilde{\varvec{\theta }})$ is the likelihood density function determined by ${\textbf{F}}$ in (3.5) and assumptions on $\widetilde{{\mathcal {E}}}$, $p({\textbf{f}}\,|\,\widetilde{\varvec{\theta }})$ is the density of the prior distribution encoding a priori assumptions about the solution, and $p(\widetilde{\varvec{\theta }})$ is the hyperprior density for all other involved parameters, which we denote collectively as $\widetilde{\varvec{\theta }}$. As was also done in Sect. 4, we write $p(\widetilde{\varvec{\theta }}) = p(\widetilde{\gamma }) \, p(\beta )$, where $\widetilde{\gamma }$ and $\beta$ correspond to the inverse noise and inverse prior variances respectively.

5.2 Formulating the Likelihood

Since $\widetilde{{\mathcal {E}}} \sim {\mathcal {C}}{\mathcal {N}}({{\textbf{0}}},\widetilde{\gamma }^{-1} {\textbf{I}}_N)$ for unknown variance $\widetilde{\gamma }^{-1}$, we have

$$\begin{aligned} p(\widetilde{{\varvec{\epsilon }}} \,| \, \widetilde{\gamma })= \left( \frac{\widetilde{\gamma }}{\pi }\right) ^{N}\exp \left( -\widetilde{\gamma } \Vert \widetilde{{\varvec{\epsilon }}} \Vert _2^2 \right) . \end{aligned}$$

It follows from (3.5) that the likelihood density function is then

$$\begin{aligned} p(\widehat{{\textbf{b}}}\,|\,{\textbf{f}},\widetilde{\gamma }) = \left( \frac{\widetilde{\gamma }}{\pi }\right) ^{N}\exp (-\widetilde{\gamma } \Vert \widehat{{\textbf{b}}} - {\textbf{F}}\, {\textbf{f}}\Vert _2^2), \end{aligned}$$

(5.3)

with corresponding distribution

$$\begin{aligned} \widehat{{\mathcal {B}}} \sim {\mathcal {C}}{\mathcal {N}}({\textbf{F}}\, {\textbf{f}}, \widetilde{\gamma }^{-1} {\textbf{I}}_N ). \end{aligned}$$

(5.4)

We note that the factor of 2 difference in (5.3) from (4.4) is due to the noise now being complex-valued.

5.3 Formulating the Prior and the Hyperpriors

For reasons already mentioned, we again choose the prior density function to be used in (5.2) as (4.7). We also note that in the context of the likelihood density function given by (5.3), our choice of prior means that the resulting objective function yields enough overlap between the data (likelihood) and regularization (prior) terms to determine a meaningful solution, beyond satisfying the common kernel condition.⁹ Specifically, for $r > 0$ and constants $Const_1, C > 0$, (2.8) yields

$$\begin{aligned}\langle P_{m}^{\lambda } f - f, e^{i k \pi x} \rangle \le Const_1 \cdot {e^{-m^r}} \int _{-1}^1 e^{-ik\pi x}dx < Ce^{-rm},\end{aligned}$$

and in fact is only nonzero for $k = 0$. Since $m \propto N$, which is assumed to adequately resolve the underlying signal ${\textbf{f}}$ from $\widehat{{\textbf{b}}}$, we conclude that the solution ${\textbf{f}}$ can be recovered for our choice of prior. Furthermore, although only $\lambda \ge 0$ is required to satisfy (2.8), as discussed in Remark 4.3, $\lambda$ still must be large enough for (3.9) to accurately approximate $\{\widehat{f}^\lambda _\ell \}_{\ell = 1}^m$ in (2.7), while small enough to maintain robustness. A more detailed discussion for choosing the Gegenbauer parameters in the context of noise is provided in Sect. 6.3.

Finally, the hyperpriors $\widetilde{\gamma }$ and $\beta$ are again modeled as Gamma distributions, yielding the hyperprior density function (4.10) density function with $\widetilde{\gamma }$ replacing $\gamma$ as the likelihood hyperprior, i.e.

$$\begin{aligned} p(\widetilde{\varvec{\theta }}) = p(\widetilde{\gamma })p(\beta ) \propto \widetilde{\gamma }^{c-1} \exp (-d \, \widetilde{\gamma }) \, \beta ^{c-1} \exp (-d \, \beta ). \end{aligned}$$

(5.5)

5.4 Bayesian Inference

Substituting the likelihood (5.3), the prior (4.7) and the hyperprior (5.5) density functions into (5.2), we obtain the posterior density function approximation

$$\begin{aligned} p({\textbf{f}}, \widetilde{\gamma }, \beta \, \vert \, \widehat{{\textbf{b}}} )\propto & \widetilde{\gamma }^ {c+N-1} \beta ^{c+\frac{N}{2} -1} \exp \bigg \{ -\widetilde{\gamma } \Vert \widehat{{\textbf{b}}} - {\textbf{F}}\, {\textbf{f}}\Vert _2^2 \nonumber \\ & -\frac{\beta }{2} \Vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}){\textbf{f}}\Vert _2^2 -d \, \widetilde{\gamma } -d \, \beta \bigg \}. \end{aligned}$$

(5.6)

The MAP estimate of (5.6) is the minimizer of the objective function

$$\begin{aligned} \widetilde{{\mathcal {J}}}({\textbf{f}}, \widetilde{\gamma }, \beta )= & -(c+N-1) \log (\widetilde{\gamma }) -(c+\frac{N}{2}-1) \log (\beta ) + \widetilde{\gamma } \Vert \widehat{{\textbf{b}}} - {\textbf{F}}\, {\textbf{f}}\Vert _2^2 \nonumber \\ & + \frac{\beta }{2} \Vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) {\textbf{f}}\Vert _2^2 +d \, \widetilde{\gamma } +d \,\beta \end{aligned}$$

(5.7)

up to a constant that is independent of ${\textbf{f}}$, $\widetilde{\gamma }$, and $\beta$. The BCD algorithm iteratively updates the solution according to

$$\begin{aligned} & \displaystyle \left( 2\widetilde{\gamma } \, {{\textbf{F}}}^{*} {{\textbf{F}}} + \beta \,({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) ^ T ({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT})\right) {\textbf{f}}= 2\widetilde{\gamma } \, {{\textbf{F}}}^{*} \, \widehat{{\textbf{b}}}, \end{aligned}$$

(5.8a)

$$\begin{aligned} & \displaystyle \widetilde{\gamma } = \frac{c+N-1}{\Vert \widehat{{\textbf{b}}} - {\textbf{F}}\, {\textbf{f}}\Vert _2^2+d}, \end{aligned}$$

(5.8b)

$$\begin{aligned} & \displaystyle \beta = \frac{2c+N-2}{ \Vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) {\textbf{f}}\Vert _2^2+2d}. \end{aligned}$$

(5.8c)

Here (5.8a) is equivalent to updating ${\textbf{f}}$ via the quadratic optimization problem

$$\begin{aligned} {\textbf{f}}= \underset{{\textbf{f}}}{\text {arg min}} \left\{ \widetilde{\gamma } \Vert \widehat{{\textbf{b}}} - {\textbf{F}}\, {\textbf{f}}\Vert _2^2 +\frac{\beta }{2} \Vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg} {\textbf{F}}^{CT}) {\textbf{f}}\Vert _2^2 \right\} . \end{aligned}$$

(5.9)

Algorithm 3 summarizes the iterative process for minimizing the objective function (5.7), which provides the point estimate solution ${\textbf{f}}$ along with precision values $\widetilde{\gamma }$ and $\beta$. Analogous to the formulation obtained in Remark 4.7, for fixed $\widetilde{\gamma }$ and $\beta$ it is possible to directly sample from the resulting posterior to obtain credible intervals.

6 Numerical Experiments

We now demonstrate the efficacy of the BSR (Algorithm 2) and GBSR (Algorithm 3), and compare each method’s performance to the original spectral reprojection in Algorithm 1. We also test our new methods for varying signal-to-noise ratio (SNR), which we define as

$$\begin{aligned} \text {SNR} = 10 \log _{10} \left( \frac{\Vert {\textbf{F}}{\textbf{f}}\Vert _2^2}{N \alpha ^{-1}}\right) . \end{aligned}$$

(6.1)

In each example the noisy Fourier data $\widehat{{\textbf{b}}}$ is given by (2.1) with noise variance $\alpha ^{-1}$ corresponding to (6.1). The noiseless N Fourier coefficients $\widehat{{\textbf{f}}}$ are constructed via trapezoidal rule (3.1) for a highly resolved mesh (8N).

6.1 An Illustrative Example

We first seek to make a general comparison of the Fourier partial sum approximation given by (3.6), the (Gegenbauer) spectral reprojection in Algorithm 1, the BSR approach in Algorithm 2, and finally the GBSR method in Algorithm 3. We choose an example that is readily recovered for large enough N (number of given Fourier coefficients) in the noise-free case using spectral reprojection for suitable parameter choices m and $\lambda$. In particular, we consider the function

$$\begin{aligned} f(x)=e^x \sin (5x), \quad x \in [-1,1]. \end{aligned}$$

(6.2)

We assume we are given the first $N = 128$ noisy Fourier samples $\widehat{{\textbf{b}}}$ in (2.1) with noise variance $\alpha ^{-1} = 2 \times 10^{-3}$ (equivalently SNR $\approx 5.95$). The spectral reprojection parameters $m=9$ and $\lambda =4$ are chosen to satisfy Theorem 1 and also to ensure accurate and robust recovery in the noise-free case.

Fig. 1

Recovery of $f(x) = e^x\sin {(5x)}$. (left) Fourier reconstruction ${\textbf{f}}_N$ in (3.6); (center-left) Spectral reprojection ${\textbf{f}}_{m,N}^{\lambda }$ in Algorithm 1; (center-right) ${\textbf{f}}_{BSR}$ in Algorithm 2; and (right) ${\textbf{f}}_{GBSR}$ in Algorithm 3

Figure 1 compares the recovery of (6.2) using (3.6), Algorithms 1, 2 and 3. The $99.9\%$ credible intervals of the solution posterior $p({\textbf{f}}\,|\, \widehat{{\textbf{b}}})$ using the final (fixed) estimates of the hyperparameters $\widetilde{\gamma }$ and $\beta$, as described in Remark 4.7, are also displayed. In addition to the Gibbs phenomenon artifacts manifested by the over/undershoots at the boundaries, the Fourier partial sum ${\textbf{f}}_N$ clearly yields a noisy approximation. Standard filtering would reduce the oscillations, but also cause excessive blurring [29]. Algorithm 1 improves accuracy away from the boundaries, but due to the added noise there are large deviations at the boundaries, especially near $x=-1$. In this regard we note that it was shown in [5] that the variance near the boundaries using the Gegenbauer reconstruction method is not reduced when compared to the standard Fourier partial sum. As expected, the point estimate in Algorithm 2 yields nearly identical results to those obtained in Algorithm 1. The corresponding credible intervals obtained for fixed hyperparameters $\gamma$ and $\beta$ (see Remark 4.7) are very tight and therefore not shown. This is also to be expected following the discussion at the beginning of Sect. 5, and indeed served to motivate the GBSR approach. Finally, we observe that Algorithm 3 yields the overall best results, with better performance throughout the domain. The credible interval is also displayed in Fig. 1(right).

Remark 6.1

Due to issues of ill conditioning leading to the Runge phenomenon, the Gegenbauer spectral reprojection may perform poorly for large $\lambda$ even though Theorem 1 is satisfied [11]. The robust Gibbs complementary (Freud) basis proposed in [20] as the reprojection basis $\{\psi _l^\lambda \}_{l = 0}^m$ in (2.4) helps alleviate these issues, but requires more points-per-wave (large N) to fully resolve the approximation. The approach moreover was considered only for noise-free data. Using the Freud reprojection basis did not yield any noticeable improvement in our experiments. Therefore, given the additional cost incurred in using large N, we do not consider it further.

6.2 Noise Analysis

Now we investigate a more typical scenario in computational inverse problems, that is, with fewer observables and possibly lower SNR. Since it was used in [26], we also consider the non-periodic analytic function $f(x)=\cos (1.4\pi (x+1))$ on domain $[-1,1]$. We assume we are given $N = 48$ noisy Fourier coefficients $\widehat{{\textbf{b}}}$ in (2.1) with different SNR levels, where $\widehat{{\textbf{f}}}$ are constructed from (3.1) using a refined mesh 8N.

Remark 6.2

(Noisy versus noise-free data) For the noiseless case, it was shown in [26] that choosing $m = \lambda = 9$ yields more accurate results given $N = 48$ Fourier coefficients $\widehat{{\textbf{f}}}$.¹⁰ However, when the Fourier coefficients contain even small amounts of noise, the performance quality of the spectral reprojection method rapidly deteriorates. In particular, the ill-conditioning attributed to larger values of $\lambda$ exacerbates the impact of noise in the approximation [5]. To mitigate these effects we choose $\lambda = 4$ in our numerical experiments. Note that m, which corresponds to the number of Gegenbauer polynomials needed to resolve the underlying function, is less impacted by noise. Hence $m = 9$ is still appropriate.

Fig. 2

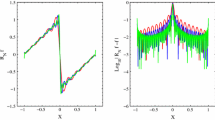
(Top-left) Fourier reconstruction ${\textbf{f}}_N$ in (3.6) for $N = 48$; (top-middle) Spectral reprojection ${\textbf{f}}_{m,N}^{\lambda }$ computed via Algorithm 1 for $\lambda =4$ and $m = 9$; (top right) pointwise log errors for $\lambda =4$ and $\lambda =2$ for noiseless data. (Bottom) Same experiments with SNR $= 10$

To serve as baseline comparisons for the GBSR method, Fig. 2(top) shows the Fourier partial sum in (3.6) and the Gegenbauer reconstruction obtained from Algorithm 1 given noiseless Fourier data. The pointwise errors in logarithmic scale for $\lambda =4$ and $\lambda =2$ are also shown. Clearly, Gegenbauer reconstruction successfully resolves the Gibbs phenomenon for appropriate choices of $\lambda$ and m according to Theorem 1, with $\lambda = 4$ providing a more accurate approximation than $\lambda = 2$. Figure 2(bottom) shows the same results for SNR $= 10$. The performance of Gegenbauer reconstruction notably deteriorates, especially near the boundaries, which is attributable to the Runge phenomenon being exacerbated by noise. In this case we observe that $\lambda =2$ yields better overall performance, and noticeably at the boundaries. Section 6.3 provides a more in depth discussion regarding the relationship between SNR and $\lambda$.

Fig. 3

Log error plots for varying SNR: (left) $l_2$ error in $[-1,1]$, (middle-left) at $x=-1$; (middle-right) at $x=-0.8$; and (right) $l_2$ error in $[-.5,.5]$ for ${\textbf{f}}_N$, ${\textbf{f}}_{m,N}^\lambda$ ${\textbf{f}}_{BSR}$, and ${\textbf{f}}_{GBSR}$

Figure 3 compares errors in logarithmic scale as a function of SNR throughout the interval $[-1,1]$, at the boundary $x=-1$, at the point $x=-0.8$, and in the interior region from $x=-0.5$ to $x=-0.5$ (chosen to show overall error away from the boundaries). We observe that with increasing SNR, the Gegenbauer approximation ${\textbf{f}}_{m,N}^\lambda$ in Algorithm 1 starts to converge, as is consistent with Fig. 2(right). We note that by construction the point estimate of the BSR method in Algorithm 2 is essentially equivalent to the original Gegenbauer reconstruction approximation. The Fourier partial sum and the GBSR method also produce more accurate approximations with increasing SNR, although as expected each method’s convergence rate is not clearly established. The $l_2$ error in $[-1,1]$ for all approximations is obviously dominated by the maximum error occurring at $x = -1$. The advantage in using spectral reprojection becomes more apparent away from the boundary, especially with increasing SNR. At $x = -.8$ the GBSR does not yield improvement from standard Fourier reconstruction, even in low SNR environments. By contrast, once we are far enough from the boundary, using Algorithm 3 yield more accurate solutions for low SNR. To summarize, in the low SNR regime, the Gegenbauer reconstruction method does not satisfy the conditions for obtaining numerical convergence, especially near the boundary. In this case, the GBSR method provides a relatively reasonable approximation, as well as uncertainty quantification.

Fig. 4

Pointwise log likelihood and prior term plots for SNR = 2 (left), 10 (middle-left), 20 (middle-right) and 40 (right)

Fig. 5

Log hyperparameter values for varying SNR

Figure 4 displays the BSR pointwise likelihood term $\vert {\textbf{f}}_{m,N}^\lambda - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}{\textbf{f}}\vert$ and prior term $\vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}){\textbf{f}}\vert$ in logarithmic scale for SNR = 2, 10, 20, and 40. The GBSR prior term, $\vert ({\textbf{I}}_{N} - {\textbf{F}}^{Geg}{\textbf{F}}^{CT}){\textbf{f}}\vert$, is also shown. Since the GBSR likelihood term $\vert \widehat{{\textbf{b}}} - {\textbf{F}}\, {\textbf{f}}\vert$ is in the Fourier domain, it is not included here. While none of these terms directly correspond to the solution errors, they represent the quantities being minimized in the optimization problems (4.19) and (5.9) respectively. Observe that the BSR prior term varies considerably from the boundary, $x = -1$, and the rest of the domain. This is consistent with the goals for the original Gegenbauer reconstruction method [27], which is to “clamp down” the effects from the Gibbs oscillations at the boundary while retaining spectral accuracy throughout the domain. In addition, the magnitude of the BSR likelihood term does not vary significantly with respect to different SNR levels. In other words, the amount of noise in the system does not play an important role in the likelihood term of the BSR method. We can again understand this behavior from the theoretical results for the original Gegenbauer reconstruction method, that is, high frequency information – in this case including noise – is projected into the null space. While the projection operation is a desired property for the forward approach, it introduces more ambiguity in the recovery of the underlying signal, leading to less versatility in solving the inverse problem. This behavior can also be observed in the hyperparameter values for varying SNR, shown in logarithmic scale in Fig. 5. Once again we see that the hyperparameter for the BSR likelihood term $\gamma$ does not change significantly as a function of SNR. On the other hand, the hyperparameter for the GBSR likelihood term ${\tilde{\gamma }}$ clearly increases with SNR, indicating that the GBSR likelihood term, which is in the Fourier domain, directly reflects the noise level. This observation motivates the potential use of a spatially varying hyperparameter to further improve the performance of the BSR method, which will be explored in future work.

6.3 Relationship Between SNR and Gegenbauer Parameters

Fig. 6

Log error plots for varying $\lambda$: $l_2$ error in $[-1,1]$ with SNR value 2 (left), 10 (middle) and 30 (right) for ${\textbf{f}}_N$, ${\textbf{f}}_{m,N}^\lambda$ ${\textbf{f}}_{BSR}$, and ${\textbf{f}}_{GBSR}$

Theorem 1 establishes the relationship between the number of Fourier coefficients N, the expansion degree in the Gegenbauer polynomial basis m and the corresponding weighting parameter $\lambda$. It does not discuss the relationship between these parameters and SNR, however. By design, the BSR method yields MAP estimates that behave similarly to the Gegenbauer reconstruction solution. Specifically, parameters that satisfy Theorem 1 yield the best approximations, with $\lambda = \kappa N$ required for small error $E_D$ being analogous to the likelihood term (4.3). On the other hand, $\lambda = \kappa N$ is not required for the GBSR method according to its likelihood distribution (5.4). For both methods, when the observables are practically noise-free, there is some non-negligible contribution in using the trapezoidal rule (3.9) for small $\lambda$, especially for small N. In all cases, m must be chosen large enough to resolve the underlying function. In this regard it is important to point out that the parameter m is what describes our prior belief, specifically the assumption that a smooth function can be well-approximated by its corresponding orthogonal polynomial partial sum expansion (2.4). It follows that for $m = 0$ we assume the function is constant, for $m = 1$, the function is linear, etc. Indeed, $m = 0$ and $m = 1$ correspond more closely to what is often assumed for image recovery. By contrast, the BSR and GBSR enable the recovery of functions with much greater variability (as dictated by m).

While the choice of m is somewhat independent of SNR, how $\lambda$ might be chosen changes significantly as SNR decreases. First, any error made using trapezoidal rule is insignificant in low SNR environments. Second, as already discussed, the variance of the Gegenbauer reconstruction method increases at the boundaries. Coupled with the ill-conditioning effects for larger choices of $\lambda$, it is not clear how the value of $\lambda$ affects the performance of each method.

To emphasize the effects of noise on the choice of $\lambda$, we consider the same example in Sect. 6.2 for varying (integer) values of $\lambda$ and fixed SNR of 2, 10,  and 30. As before we are given $N = 48$ noisy Fourier coefficients $\widehat{{\textbf{b}}}$ in (2.1) and we again choose $m = 9$ for $\lambda \in [1,8]$.

Figure 6 compares the $l_2$ error in $[-1,1]$ in logarithmic scale with respect to different $\lambda$ for SNR $= 2, 10$ and 30. No theoretical justification is available for applying any of these methods in low SNR environments. As SNR increases, it becomes more evident that an optimal $\lambda$ for both the Gegenbauer reconstruction and BSR methods exists, and is a cumulative result of all the possible considerations already mentioned. On the other hand, the GBSR method is clearly robust for various $\lambda$ values in low SNR environments, mainly because the likelihood term does not involve its use. Of course, none of these methods are a panacea in low SNR environments. The GBSR and BSR methods provide additional uncertainty quantification for fixed hyperparameters, although by design the BSR credible interval is quite narrow.

Fig. 7

Credible intervals with ${\textbf{f}}_{BSR}$ and ${\textbf{f}}_{GBSR}$ for SNR value 2 (left), 10 (middle) and 30 (right) and $\lambda =2$ (top and middle-top), $\lambda =4$ (middle-bottom and bottom)

We illustrate this in Fig. 7, where the BSR and GBSR approximations are provided along with their respective credible intervals for $\lambda = 2, 4$. Consistent with Fig. 6, the BSR provides the most accurate results for $\lambda = 2$. The credible interval is very narrow, even in low SNR environments and almost impossible to discern for SNR = 10 and 30. By contrast, we observe nearly identical estimations for $\lambda = 2, 4$ when using GBSR. There is furthermore additional information to be gleaned from their credible intervals. Moreover the error near the boundaries appears to be dominated by the likelihood term also having a larger error there, attributable to the over/undershoots caused by the Gibbs phenomenon, as opposed to simply noise (see Fig. 2(left)).

We emphasize that our numerical experiments are not meant to be prescriptive—that is, it is not the case that one method always outperforms another in all environments. This is to be expected, since Theorem 1 has already identified the best solution in the noiseless case. Rather we demonstrate how spectral reprojection inspires two Bayesian approaches, BSR and GBSR, both of which can recover analytic non-periodic functions from noisy Fourier data and provide some uncertainty quantification. Indeed, our results suggest that there is justification for choosing a hybrid BSR/GBSR approach, one that weighs the BSR more heavily near the boundaries and GBSR more heavily in the interior. It is also possible to modify the BSR method so that the likelihood and prior use different parameters for m and $\lambda$, which also can be analyzed in the context of the proof of Theorem 1. These and other ideas will be explored in future investigations.

7 Concluding Remarks

In this investigation we proposed the Bayesian spectral reprojection (BSR) and generalized Bayesian spectral reprojection (GBSR) inference methods to recover smooth non-periodic functions from given noisy Fourier data. Both method are motivated by the theoretical convergence analysis provided for the spectral reprojection method given noiseless data. These insights are brought into a statistical framework to effectively combine numerical analysis with uncertainty quantification.

The BSR approach provides a statistical framework for the spectral reprojection method, enabling a better understanding of the limitations for using spectral reprojection in noisy environments. The likelihood and prior terms follow directly from the error analysis established for the original (noiseless) spectral reprojection method in [27]. By design, the BSR yields estimates similar to the Gegenbauer reconstruction method, while also providing uncertainty quantification for fixed hyperparameters. As both the likelihood and prior terms are related to Gegenbauer polynomials, the approach limits the space of possible solutions, resulting in very narrow credible intervals. Furthermore, the approximation quality for both spectral reprojection and BSR rapidly deteriorate with decreasing SNR.

The GBSR approach is then proposed to expand the space of possible solutions, which is accomplished by incorporating the Fourier data directly into the likelihood term (as opposed to first transforming the data to the space of mth-degree Gegenbauer polynomials). In this regard the GBSR provides a more natural construction for computational linear inverse problems. The resulting approximation is more robust with respect to the Gegenbauer polynomial weighting parameter $\lambda$, especially in low SNR environments. By design it cannot achieve the same accuracy for high SNR, as the error from the likelihood term is still large due to the effects of the Gibbs phenomenon. The best accuracy for the limiting case of no noise is already obtained using spectral reprojection.

There are clearly benefits and drawbacks in using both the BSR and GBSR, depending on SNR and Gegenbauer weight $\lambda$. Importantly, these benefits and drawbacks are highly predictable by the construction of each method and theoretical motivation in [27] (along with the well-known properties of Fourier reconstruction for non-periodic functions). Because of this, developing a hybrid approach that does not require additional user inputs is completely attainable.