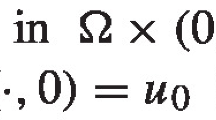Abstract
A notable feature of the anomalous sub-solution equation is its solution’s algebraic decay over extended time periods, a phenomenon commonly associated with Mittag-Leffler type stability. For power-nonlinear sub-diffusion models with variable coefficients, we prove Mittag-Leffler stability under natural decay assumptions on the source functions, with decay rate \(\Vert u(t)\Vert _{L^{s}(\Omega )}=O( t^{-(\alpha +\beta )/\gamma } )\) as \(t\rightarrow \infty \), where \(\alpha \), \(\gamma \) are positive constants, \(\beta \in (-\alpha ,\infty )\) and \(s\in (1,\infty )\). We then develop a structure-preserving algorithm for these models. For the complete monotonicity-preserving (\(\mathcal{C}\mathcal{M}\)-preserving) schemes developed by Li and Wang (Commun. Math. Sci., 19(5):1301-1336, 2021), we show they satisfy the discrete comparison principle for time-fractional differential equations with variable coefficients. By carefully constructing the fine the discrete supersolutions and subsolutions, we obtain the numerical solution’s long-time optimal decay rate \(\Vert u_{n}\Vert _{L^{s}(\Omega )}=O( t_n^{-(\alpha +\beta )/\gamma } )\) as \(t_{n}\rightarrow \infty \), which aligns perfectly with the theoretical decay rate. Finally, we validate our analysis through numerical experiments.



Similar content being viewed by others

Data Availability
No data was used for the research described in the article.
Notes
As usual, our notation \(\sim \) here represents the asymptotic limit \(\lim _{t\rightarrow \infty } \frac{\langle x^2(t)\rangle }{t}=C\), where C represents a general positive constant, which may take different values in different places, but is always independent of t or n. We also use the standard notation O to represent a certain asymptotic order, for example \(y(t)=O(t^{-\alpha })\) means \(\lim _{t\rightarrow \infty } \left| \frac{y(t)}{t^{-\alpha }}\right| \le C\).
A function \(g(t): (0, \infty )\rightarrow \mathbb {R}\) is said to be completely monotone if \((-1)^n g^{(n)}(t)\ge 0\) for all \(n\ge 0\) and \(t>0\).
References
Bologna, M., Svenkeson, A., West, B.J., Grigolini, P.: Diffusion in heterogeneous media: an iterative scheme for finding approximate solutions to fractional differential equations with time-dependent coefficients. J. Comput. Phys. 293, 297–311 (2015)
Boudjeriou, T.: Decay estimates and extinction properties for some parabolic equations with fractional time derivatives. Fract. Calc. Appl. Anal. 27, 393–432 (2024)
Costa, F.S., Oliveira, E.C., Plata, A.R.G.: Fractional diffusion with time-dependent diffusion coefficient. Rep. Math. Phys. 87, 59–79 (2021)
Dipierro, S., Valdinoci, E., Vespri, V.: Decay estimates for evolutionary equations with fractional time-diffusion. J. Evol. Equ. 19, 435–462 (2019)
Fa, K.S., Lenzi, E.K.: Time-fractional diffusion equation with time dependent difussion coefficient. Phys. Rev. E 72, 011107 (2005)
Feng, Y.Y., Li, L., Liu, J.G., Tang, T.: Some grönwall inequalities for a class of discretizations of time fractional equations on nonuniform meshes. SIAM J. Numer. Anal. 62, 2196–2221 (2024)
Gilbarg, D., Trudinger, N.: Elliptic partial differential equations of second order. Springer, Berlin, Heidelberg (2001)
Hernández, D., Herrera-Hernández, E.C.: Non-local diffusion models for fractured porous media with pressure tests applications. Adv. Water Resour. 149, 103854 (2021)
Hristov, J.: Subdiffusion model with time-dependent diffusion coefficient: Integral-balance solution and analysis. Therm. Sci. 21, 69–80 (2017)
Jin, B.: Fractional differential equations: An approach via fractional derivatives. Springer, Cham (2021)
Jin, B., Zhou, Z.: Numerical treatment and analysis of time-fractional evolution equations. Springer Nature (2023)
Kemppainen, J., Zacher, R.: Long-time behavior of non-local in time Fokker-Planck equations via the entropy method. Math. Models Methods Appl. Sci. 29, 209–235 (2019)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and applications of fractional differential equations. Elsevier (2006)
Li, L., Liu, J.G.: A discretization of Caputo derivatives with application to time fractional SDEs and gradient flows. SIAM J. Numer. Anal. 57, 2095–2120 (2019)
Li, L., Wang, D.L.: Complete monotonicity-preserving numerical methods for time fractional odes. Commun. Math. Sci. 19, 1301–1336 (2021)
Smadiyeva, A.G., Torebek, B.T.: Decay estimates for the time-fractional evolution equations with time-dependent coefficients. Proc. R. Soc. A 479, 381–397 (2023)
Vergara, V., Zacher, R.: Optimal decay estimates for time-fractional and other nonlocal subdiffusion equations via energy methods. SIAM J. Math. Anal. 47, 210–239 (2015)
Wang, D.L., Stynes, M.: Optimal long-time decay rate of numerical solutions for nonlinear time-fractional evolutionary equations. SIAM J. Numer. Anal. 61, 2011–2034 (2023)
Wang, D.L., Zou, J.: Mittag-Leffler stability of numerical solutions to time fractional odes. Numer. Algorithms 92, 2125–2159 (2023)
Zacher, R.: Boundedness of weak solutions to evolutionary partial integro-differential equations with discontinuous coefficients. J. Math. Anal. Appl. 348, 137–149 (2008)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest:
The authors declare that they have no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The research of Dongling Wang is supported in part by NSFC (No. 12271463) and Outstanding Youth Foundation of Department of Education in Hunan Province (No.22B0173).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Dong, W., Wang, D. Mittag-Leffler Stability of Complete Monotonicity-Preserving Schemes for Sub-Diffusion Equations with Time-Dependent Coefficients. J Sci Comput 102, 82 (2025). https://doi.org/10.1007/s10915-025-02812-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-025-02812-5