Skip to main content
Springer Nature Link
Log in

Auto-Weighted Multiple Graph Regularized Non-negative Tensor Tucker Decomposition for Clustering

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

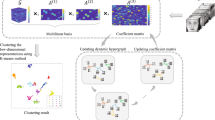
Non-negative Tucker decomposition (NTD) has received much attention due to its efficient processing of high-dimensional non-negative data. To preserve the intrinsic geometric structure of the data, various graph regularization NTD methods have been proposed. However, most existing methods rely on single graph regularization, limiting their flexibility and adaptability, since a single graph may not adequately capture the intrinsic manifold structure of various datasets. To address this problem, this paper introduces an auto-weighted multiple graph structure as the regularizer for NTD, and then proposes a novel method called auto-weighted multiple graph regularized non-negative Tucker decomposition (AMGRNTD). The AMGRNTD method utilizes a linear combination of multiple simple graphs to more effectively preserve the intrinsic manifold structure of the original data, offering greater applicability to practical problems than single graph-based methods. Furthermore, the AMGRNTD method automatically learns an optimal weight for each graph without additional parameters. Experimental results on four real-world datasets demonstrate that the proposed method achieves better performance in image clustering than some existing state-of-the-art graph-based regularization methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Algorithm 1
Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data Availability

The datasets generated during the current study are available from the corresponding author upon reasonable request.

Code Availability

The code is available upon reasonable request and addressed to the corresponding author.

Notes

  1. Available at https://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php.

  2. Available at https://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html.

  3. Available at https://www.anefian.com/research/face_reco.htm.

  4. Available at http://www.cad.zju.edu.cn/home/dengcai/Data/MLData.html.

References

  1. Panagakis, Y., Kossaifi, J., Chrysos, G.G., Oldfield, J., Nicolaou, M.A., Anandkumar, A., Zafeiriou, S.: Tensor methods in computer vision and deep learning. Proc. IEEE 109(5), 863–890 (2021)

    Article  Google Scholar 

  2. Sandoval, B., Barocio, E., Korba, P., Sevilla, F.R.S.: Three-way unsupervised data mining for power system applications based on tensor decomposition. Electric Power Systems Res. 187, 106431 (2020)

    Article  MATH  Google Scholar 

  3. Sidiropoulos, N.D., De Lathauwer, L., Fu, X., Huang, K., Papalexakis, E.E., Faloutsos, C.: Tensor decomposition for signal processing and machine learning. IEEE Trans. Signal Process. 65(13), 3551–3582 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  4. Salem, N., Hussein, S.: Data dimensional reduction and principal components analysis. Proc. Comput. Sci. 163, 292–299 (2019)

    Article  MATH  Google Scholar 

  5. Martinez, A.M., Kak, A.C.: PCA versus LDA. IEEE Trans. Pattern Anal. Mach. Intell. 23(2), 228–233 (2001)

    Article  Google Scholar 

  6. Zhou, G., Cichocki, A., Zhang, Y., Mandic, D.P.: Group component analysis for multiblock data: common and individual feature extraction. IEEE Trans. Neural Netw. Learning Syst. 27(11), 2426–2439 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  7. Lee, D.D., Seung, H.S.: Learning the parts of objects by non-negative matrix factorization. Nature 401(6755), 788–791 (1999)

    Article  MATH  Google Scholar 

  8. Cai, D., He, X., Han, J., Huang, T.S.: Graph regularized non-negative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 33(8), 1548–1560 (2010)

    MATH  Google Scholar 

  9. Geng, B., Tao, D., Xu, C., Yang, L., Hua, X.-S.: Ensemble manifold regularization. IEEE Trans. Pattern Anal. Mach. Intell. 34(6), 1227–1233 (2012)

    Article  MATH  Google Scholar 

  10. Wang, J.J.Y., Bensmail, H., Gao, X.: Multiple graph regularized non-negative matrix factorization. Pattern Recogn. 46(10), 2840–2847 (2013)

    Article  MATH  Google Scholar 

  11. Nie, F., Li, J., Li, X.: Parameter-free auto-weighted multiple graph learning: a framework for multiview clustering and semi-supervised classification. IJCAI 9, 1881–1887 (2016)

    MATH  Google Scholar 

  12. Shu, Z., Wu, X., Fan, H., Huang, P., Wu, D., Hu, C., Ye, F.: Parameter-less auto-weighted multiple graph regularized non-negative matrix factorization for data representation. Knowl. Based Syst. 131, 105–112 (2017)

    Article  MATH  Google Scholar 

  13. Tucker, L.R.: Some mathematical notes on three-mode factor analysis. Psychometrika 31(3), 279–311 (1966)

    Article  MathSciNet  MATH  Google Scholar 

  14. Yang, Z., Zhang, Y., Xiang, Y., Yan, W., Xie, S.: Non-negative matrix factorization with dual constraints for image clustering. IEEE Trans. Syst. Man Cybernet. Syst. 50(7), 2524–2533 (2018)

    Article  MATH  Google Scholar 

  15. Song, H.A., Kim, B.K., Xuan, T.L., Lee, S.Y.: Hierarchical feature extraction by multi-layer non-negative matrix factorization network for classification task. Neurocomputing 165, 63–74 (2015)

    Article  MATH  Google Scholar 

  16. Pascual-Montano, A., Carmona-Saez, P., Chagoyen, M., Tirado, F., Carazo, J.M., Pascual-Marqui, R.D.: bioNMF: a versatile tool for non-negative matrix factorization in biology. BMC Bioinformatics 7, 1–9 (2006)

    Article  MATH  Google Scholar 

  17. Kim, Y.D., Choi, S.: Nonnegative tucker decomposition, 2007 IEEE Conference on Computer Vision and Pattern Recognition, 1–8 (2007)

  18. Kim, Y.D., Cichocki, A., Choi, S.: Non-negative Tucker decomposition with alpha-divergence, 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, 1829–1832 (2008)

  19. Yin, W., Ma, Z.: LE &LLE regularized non-negative Tucker decomposition for clustering of high dimensional datasets. Neurocomputing 364, 77–94 (2019)

  20. Jiang, T., Ng, M.K., Pan, J., Song, G.: Non-negative low rank tensor approximations with multidimensional image applications. Numer. Math. 153(1), 141–170 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  21. Jiang, B., Ding, C., Tang, J., Luo, B.: Image representation and learning with graph-Laplacian Tucker tensor decomposition. IEEE Trans. Cybernet. 49(4), 1417–1426 (2018)

    Article  MATH  Google Scholar 

  22. Li, X., Ng, M.K., Cong, G., Ye, Y., Wu, Q.: MR-NTD: manifold regularization non-negative Tucker decomposition for tensor data dimension reduction and representation. IEEE Trans. Neural Netw. Learning Syst. 28(8), 1787–1800 (2016)

    Article  MATH  Google Scholar 

  23. Qiu, Y., Zhou, G., Zhang, Y., Xie, S.: Graph regularized non-negative Tucker decomposition for tensor data representation, ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 8613–8617 (2019)

  24. Qiu, Y., Zhou, G., Wang, Y., Zhang, Y., Xie, S.: A generalized graph regularized non-negative tucker decomposition framework for tensor data representation. IEEE Trans. Cybernet. 52(1), 594–607 (2020)

    Article  MATH  Google Scholar 

  25. Liu, Q., Lu, L., Chen, Z.: Non-negative Tucker decomposition with graph regularization and smooth constraint for clustering. Pattern Recogn. 148, 110207 (2024)

    Article  MATH  Google Scholar 

  26. Kolda, T.G., Bader, B.W.: Tensor decompositions and applications. SIAM Rev. 51(3), 455–500 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  27. Golub, G.H., Van Loan, C.F.: Matrix Computations–4th edition, Johns Hopkins University Press, (2013)

  28. Teboulle, M., Vaisbourd, Y.: Novel proximal gradient methods for non-negative matrix factorization with sparsity constraints. SIAM J. Imag. Sci. 13(1), 381–421 (2020)

    Article  MATH  Google Scholar 

  29. Li, B., Zhou, G., Cichocki, A.: Two efficient algorithms for approximately orthogonal non-negative matrix factorization. IEEE Signal Process. Lett. 22(7), 843–846 (2014)

    MATH  Google Scholar 

  30. Zhang, Y., Zhou, G., Zhao, Q., Cichocki, A., Wang, X.: Fast non-negative tensor factorization based on accelerated proximal gradient and low-rank approximation. Neurocomputing 198, 148–154 (2016)

    Article  MATH  Google Scholar 

  31. Nazih, M., Minaoui, K., Comon, P.: Using the proximal gradient and the accelerated proximal gradient as a canonical polyadic tensor decomposition algorithms in difficult situations. Signal Process. 171, 107472 (2020)

    Article  Google Scholar 

  32. Lee, D., Seung, H.S.: Algorithms for non-negative matrix factorization. Adv. Neural Inform. Process. Syst. 13, 535–541 (2000)

    MATH  Google Scholar 

  33. Cai, D., He, X., Han, J.: Document clustering using locality preserving indexing. IEEE Trans. Knowl. Data Eng. 17(12), 1624–1637 (2005)

    Article  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the two anonymous referees for their helpful comments and suggestions.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 12471353, 12201267), the Natural Science Foundation of Gansu Province (No. 22JR5RA559).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Lanzhou University, Lanzhou, 730000, People’s Republic of China

    Guimin Liu, Bing Zheng & Fanyin Yang

  2. School of Information Engineering and Artificial Intelligence, Lanzhou University of Finance and Economics, Lanzhou, 730000, People’s Republic of China

    Ruijuan Zhao

Authors
  1. Guimin Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ruijuan Zhao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Bing Zheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Fanyin Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Bing Zheng.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, G., Zhao, R., Zheng, B. et al. Auto-Weighted Multiple Graph Regularized Non-negative Tensor Tucker Decomposition for Clustering. J Sci Comput 102, 86 (2025). https://doi.org/10.1007/s10915-025-02817-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-025-02817-0

Keywords

Mathematics Subject Classification