1 Introduction

The conservation is known to be crucial to preserve in simulating the coupled flow and transports [1]. One important example of the coupled flow and transports is the non-Newtonian flow models [2,3,4]. There are a number of numerical schemes dedicated to preserve the conservation in literature, which include the well-known mixed finite element methods [5], discontinuous Galerkin finite element methods [6] and other relevant methods [7,8,9]. The issue of mass conservation in numerical methods for flow coupled to transport can be found at [7, 10,11,12] and references cited therein. The importance of the conservation is also demonstrated to lead to the pressure robust scheme in the incompressible flow calculations (see [13, 14] and references cited therein). On the other hand, to the best knowledge of authors, only a few discussion can be found in literature that show rigorously why the locally conservative flux is important [1, 12] for the coupled flow and transports. The most rigorous discussion is believed to be at the work by Dawson, Sun and Wheeler [12]. It discusses the importance of the conservative flux for computing solutions to transports using the notion of compatibility condition imposed on the flow equation. The compatibility condition is a necessary condition for the flux to guarantee that the discrete system for the transports possesses the so-called zeroth-order accuracy. The zeroth-order accuracy means that the constant true solution can be recovered. We observe that the compatibility condition is basically the local conservation, which is a bit stronger than the standard local conservation. The standard local conservation refers to conservation of mass over a control volume or an element in a finite element or finite difference grid [8, 15, 16].

In this paper, our concern is solely restricted to the discontinuous Galerkin finite element discretization for both flow (pressure) and transports. For the sake of presentation, we shall denote the degree of polynomials used to approximate the pressure by \(k_p\) and the degree of polynomials used to approximate the solution to the transports by \(k_c\), respectively. We first introduce the concept of the local conservation (see [17,18,19]), and then investigate its relationship with the compatibility condition. More precisely, let us assume that the exact flux satisfies the continuity equation

$$\begin{aligned} \nabla \cdot \textbf{u}= f, \quad \text{ in } \Omega . \end{aligned}$$
(1)

Then for a given triangulation \(\mathcal {T}_h\) and \(k \ge 0\), we say that the numerical flux \(\textbf{U}\) is locally conservative of degree k if and only if it satisfies the following equation: for all \(T \in \mathcal {T}_h\),

$$\begin{aligned} \int _T (\nabla \cdot \textbf{U}) w \, dx = \int _T f w \, dx, \quad \forall w \in \mathbb {P}_k(T), \end{aligned}$$
(2)

where \(\mathbb {P}_k(T)\) is the polynomials on T of degree at most k. We remark that the standard local conservative flux means that it is locally conservative of degree \(k = 0\). Of course, if \(\textbf{U}\) is strongly conservative, then it is locally conservative of any degree. The construction of precisely locally conservative flux of arbitrary degree k has been discussed in [17]. Namely, the proposed local conservation is a more general version of the standard local conservation [8], but it is still weaker than the strong conservation.

The first main result in the paper is that if the numerical flux \(\textbf{U}\) satisfies the local conservation of degree \(k \ge 2k_c\), then the solution to the transports satisfies the \(L^2\) norm stability. Secondly, if the flux \(\textbf{U}\) is locally conservative of degree \(k \ge k_c\), which is exactly the compatibility condition, introduced in [12] then the zeroth-order accuracy can be obtained. Finally, for \(k_c = 0\), if the flux is locally conservative of degree \(k \ge k_c\), then the discrete solution obtained from the discontinuous Galerkin finite element scheme for the transports inherits the positivity and maximum principle preserving properties of the physical solution. We note that the locally conservative flux of degree \(k = 0\) can also be obtained by using the enriched Galerkin finite elements introduced in [7, 8]. We remark that the numerical results are traced back to that of Dawson, Sun and Wheeler [12]. Thus, the proof of the positivity and maximum principle has been elusive for many years in literature. Our technical results are based on important relationships between three schemes: the Lesaint-Raviart discontinuous Galerkin finite element method [20], the Brezzi-Marini-Süli jump stabilized discontinuous Galerkin finite element method [21] and the characteristic method along the streamline discussed in [22]. We identified a relationship between Brezzi-Marini-Süli jump stabilized discontinuous Galerkin finite element and the Characteristic method along the streamline, which is an independently interesting result. We remark that there are tremendous efforts to design positivity and maximum principle preserving scheme in literature, which include [23,24,25,26]. However, these are different schemes based on limiters. The main result of the paper strengthens the result by Dawson, Sun and Wheeler [12] and it is summarized in Table 1.

Table 1 Summary of main results
Full size table

Throughout the paper, we use the standard notation for the Sobolev spaces such as \(L^2(\Omega )\), which is the space of square integrable functions on \(\Omega \), \(H^m(\Omega )\) and \(W^{m,p}(\Omega )\) with \(1 \le m\) and \(1 \le p \le \infty \). We shall denote the discontinuous Galerkin finite element scheme simply by DG. In some cases, we shall specify the degree of polynomials used to construct DG. Namely, \(\mathrm{DG_\ell }\) refers to the discontinuous Galerkin method with polynomials of degree \(\ell \).

The rest of the paper is organized as follows. In § 2, we introduce the system of coupled flow and transports and discuss the continuous maximum and/or minimum principle. In particular, we point out how the conservative property of the flux is correlated with the establishment of the maximum principle. In § 3, we introduce the discontinuous Galerkin finite element schemes for the coupled flow and transports. The concept of the flux local conservation of degree k. In § 4, we present the relationship between the Lesaint-Raviart-DG and BMS-DG schemes. We then discuss the relationship between Lesaint-Raviart-DG scheme and the characteristic methods. These are used to establish the positivity and the maximum principle. In § 5, we present a number of numerical tests to confirm our theory and provide a concluding remark in § 6.

2 Governing Equations

In this section, we shall present the governing coupled flow and transports. We shall suppose \(\Omega \subseteq \mathbb {R}^d\) to be a bounded polygon (d = 2) or polyhedron (d = 3) with Lipschitz boundary \(\partial \Omega \). We consider the equation of conservation of mass

$$\begin{aligned} \nabla \cdot \textbf{u}= f \quad \text{ in } \Omega , \end{aligned}$$
(3)

where f is an external source/sink function such that at source, \(f > 0\) while \(f < 0\) at sink. Here the velocity \(\textbf{u}: \Omega \mapsto \mathbb {R}^d\) is defined by the Darcy’s law:

$$\begin{aligned} \textbf{u}= -\dfrac{K}{\mu (c)}\nabla p \quad \text{ in } \Omega , \end{aligned}$$
(4)

where \(p:\Omega \mapsto \mathbb {R}\) represents the pressure, K is the permeability coefficient, and \(\mu (c)\) is the fluid viscosity. Define \({\varvec{\kappa }}:= {\varvec{\kappa }}(c):= K/\mu (c)\). For the boundary, we decompose \(\partial \Omega \) into two parts \(\Gamma _D\) and \(\Gamma _N\) so that \(\overline{\partial \Omega } = \overline{\Gamma }_D \cup \overline{\Gamma }_N\) and we then impose

$$\begin{aligned} p&= g_{_D}, \quad \text{ on } \Gamma _D, \end{aligned}$$
(5a)
$$\begin{aligned} \textbf{u}\cdot \textbf{n}&= g_{_N}, \quad \text{ on } \Gamma _N, \end{aligned}$$
(5b)

where \(\textbf{n}\) denotes the outward pointing unit normal to \(\partial \Omega \), \(g_D \in L^2(\Gamma _D)\) and \(g_N \in L^2(\Gamma _N)\) are Dirichlet and Neumann boundary conditions, respectively.

We shall then consider the transport of chemically reactive species coupled with the flow equation (4) (see [12]). Transport equations for each chemical species are given as follows:

$$\begin{aligned} \partial _t (\phi c_i) + \nabla \cdot (\textbf{u}c_i - D(\textbf{u}) \nabla c_i) = f c^*_i + R_i(c_1,\cdots ,c_{n_c}), \end{aligned}$$
(6)

where \(\partial _t\) is the time derivative, \(c_i\) denotes the concentration of species \(i=1,\cdots ,n_c\) with \(n_c\) being the number of chemical species, \(D(\textbf{u})\) is the velocity-dependent diffusion/dispersion tensor which is symmetric and positive semi-definite, \(\phi \) is the volumetric factor such as porosity, and \(R_i\) is a chemical reaction term. We note that the concentration \(c^*_i=\widetilde{c}_i\) is specified at sources where \(f > 0\), while it is unknown at sinks where \(f < 0\).

The advection and diffusion of chemical species are governed by a velocity field \(\textbf{u}\), which can be shown to satisfy the continuity equation, conservation of mass equation using the fact that \(\sum _i c_i\) is constant and assuming that \(\sum _i R_i = 0\). On the other hand, following [12], we shall simply consider the single species case. Namely, we assume that the transport equation is given as follows:

$$\begin{aligned} \partial _t c + \nabla \cdot (\textbf{u}c - D(\textbf{u}) \nabla c) = fc^*, \quad&\text{ in } \Omega \times (0,\mathbb {T}], \end{aligned}$$
(7)

where \(D(\textbf{u})\) is assumed to be positive semi-definite. The boundary of \(\Omega \) for transport system, denoted by \(\partial \Omega \), is decomposed into two parts \(\Gamma _\textrm{I}\) and \(\Gamma _\textrm{O}\), the inflow and outflow boundary, respectively (i.e. \(\overline{\partial \Omega } = \overline{\Gamma }_\textrm{I} \cup \overline{\Gamma }_\textrm{O} \)). They are defined as

$$\begin{aligned} \Gamma _\textrm{I}:= \{ \textbf{x}\in \partial \Omega : \textbf{u}\cdot \textbf{n}< 0\} \quad \text{ and } \quad \Gamma _\textrm{O}:= \{ \textbf{x}\in \partial \Omega : \textbf{u}\cdot \textbf{n}\ge 0\}, \end{aligned}$$
(8)

where \(\textbf{n}\) denotes the unit outward normal vector to \(\partial \Omega \). For the boundary, we employ the following boundary conditions

$$\begin{aligned} (c\textbf{u}- D(\textbf{u}) \nabla c) \cdot \textbf{n}&= c_\textrm{I} \textbf{u}\cdot \textbf{n},&\text{ on } \Gamma _{\textrm{I}} \times (0,\mathbb {T}], \end{aligned}$$
(9a)
$$\begin{aligned} D(\textbf{u})\nabla c \cdot \textbf{n}&= 0,&\text{ on } \Gamma _{\textrm{O}} \times (0,\mathbb {T}], \end{aligned}$$
(9b)

where \(c_\textrm{I}\) is the inflow function. The initial conditions are set as \(c(\textbf{x},0) = c^0\).

2.1 Continuous Maximum Principle

In this section, we shall establish the maximum principle for the continuous case. We shall see that the continuous maximum principle is strongly affected by the continuity equation:

$$\begin{aligned} \nabla \cdot \textbf{u}= f. \end{aligned}$$
(10)

First, we define a notation for a given function \(\phi \) as follows:

$$\begin{aligned} \phi _{_+}:=\max \{\phi ,0\} \quad \text{ and } \quad \phi _{_-}:=\max \{-\phi ,0\}. \end{aligned}$$
(11)

Secondly, we show that the following continuous weak maximum principle holds under the condition that \(\textbf{u}\) satisfies the strong conservation.

Theorem 1

For the initial condition \(c^0\), the boundary condition \(c_\textrm{I}\) and specified source \(\widetilde{c}\), we let \(M=\max \{|c^0|,|c_\textrm{I}|,|\widetilde{c}|\}\). Under the condition of the strong conservation (3), we can show that the solution to equations (7)–(9) satisfies \(|c|\le M\).

Proof

By the equation (7), we have for \(v \in H^1(\Omega )\),

$$\begin{aligned} \int _\Omega \partial _t c \, v \, dx + \int _\Omega \nabla \cdot \textbf{u}c vdx +\int _\Omega \textbf{u}\cdot \nabla c \, v\,dx - \int _\Omega \nabla \cdot (D(\textbf{u}) \nabla c) v\, dx = \int _\Omega fc^*vdx. \end{aligned}$$
(12)

Using the integration by parts and the strong conservation (3), we get

$$\begin{aligned} \begin{aligned}&\int _\Omega \partial _t c \, v \, dx +\int _\Omega \textbf{u}\cdot \nabla c \, v\,dx + \int _\Omega D(\textbf{u}) \nabla c \cdot \nabla v\, dx \\&=\int _\Omega f(c^*-c)vdx+\int _{\partial \Omega }D(\textbf{u})\nabla c\cdot \textbf{n}vdx. \end{aligned} \end{aligned}$$
(13)

We shall show that \(c \le M\) by setting \(v:= (c-M)_{_+}\) in (13). We then observe that the following identity holds:

$$\begin{aligned} \begin{aligned} \int _\Omega \textbf{u}\cdot \nabla c \, v\, dx&= \int _\Omega \textbf{u}\cdot \nabla c \, (c-M)_{_+} \, dx = \frac{1}{2} \int _\Omega \nabla [(c-M)_{_+}]^2 \cdot \textbf{u}\, dx \\&=\frac{1}{2} \int _{\partial \Omega } v^2 \, \textbf{u}\cdot \textbf{n}\, ds-\frac{1}{2}\int _{\Omega }f v^2dx. \end{aligned} \end{aligned}$$
(14)

Using this identity and the boundary condition (9), the equation (13) can be shown to satisfy the following inequality:

$$\begin{aligned} \begin{aligned}&\quad \frac{1}{2} \frac{d}{dt} \int _\Omega |( c - M)_{_+}|^2 \, dx + \int _\Omega D(\textbf{u}) |\nabla (c - M)_{_+}|^2 \, dx \\&= \int _\Omega f(c^*-c)vdx +\int _{\partial \Omega } D(\textbf{u}) \nabla c\cdot \textbf{n}\, v\, ds - \frac{1}{2} \int _{\partial \Omega } v^2 \, \textbf{u}\cdot \textbf{n}\, ds + \frac{1}{2}\int _\Omega fv^2dx \\&= \int _{\Gamma _\textrm{I}} D(\textbf{u}) \nabla c\cdot \textbf{n}\, v \, ds + \int _{\Gamma _\textrm{O}} D(\textbf{u}) \nabla c\cdot \textbf{n}\, v \, ds + \int _\Omega f\left( c^*-c+\frac{1}{2}v\right) vdx \\&\quad - \frac{1}{2} \int _{\Gamma _\textrm{I}} [(c- M)_{_+}]^2 \, \textbf{u}\cdot \textbf{n}\, ds - \frac{1}{2} \int _{\Gamma _\textrm{O}} [(c- M)_{_+}]^2 \, \textbf{u}\cdot \textbf{n}\, ds \\&\le \int _{\Gamma _\textrm{I}} D(\textbf{u}) \nabla c\cdot \textbf{n}\, v \, ds - \frac{1}{2} \int _{\Gamma _\textrm{I}} [(c- M)_{_+}]^2 \, \textbf{u}\cdot \textbf{n}\, ds+ \int _\Omega f\left( c^*-c+\frac{1}{2}v\right) vdx \\&= \int _{\Gamma _\textrm{I}} \left( c-c_\textrm{I}-\frac{1}{2}(c- M)_{_+}\right) (c- M)_{_+} \, \textbf{u}\cdot \textbf{n}\, ds\\&\quad +\int _\Omega f\left( c^*-c+\frac{1}{2}(c-M)_{_+}\right) (c-M)_{_+} dx. \end{aligned} \end{aligned}$$

We shall assume \(c > M\) in some subregions. Then, we have

$$\begin{aligned} c-c_\textrm{I}-\frac{1}{2}(c- M)_{_+}=\frac{c}{2}+\frac{M}{2}-c_\textrm{I}\ge M-c_\textrm{I}\ge 0. \end{aligned}$$

Now, we consider the following identity:

$$\begin{aligned} f\left( c^*-c+\dfrac{1}{2}(c-M)_{_+}\right) (c-M)_{_+} = \left\{ \begin{array}{l} f\left( \tilde{c}-c+\dfrac{1}{2}(c-M)_{_+}\right) (c-M)_{_+}, \,\, ~~ \text{ for } f > 0 \\ \dfrac{1}{2} f (c-M)_{_+} (c-M)_{_+},\,\, ~~ \text{ for } f \le 0. \end{array} \right. \end{aligned}$$

This means

$$\begin{aligned} f\left( c^*-c+\frac{1}{2}(c-M)_{_+}\right) (c-M)_{_+} \le 0. \end{aligned}$$

Therefore, we conclude that

$$\begin{aligned} \frac{1}{2} \frac{d}{dt} \int _\Omega |( c - M)_{_+}|^2 \, dx \le 0 \end{aligned}$$
(15)

and arrive that \(c \le M\) if \(c^0 \le M\). This is a contradiction to \(c > M\) and it proves that \(c \le M\). The proof to show \(c \ge -M\) can be done by setting \(v:= (c + M)_{_-}\) in (13). The rest of the process is similar and thus, we omit the details. This completes the proof that \(|c|\le M\). \(\square \)

3 Discontinuous Galerkin Finite Element Formulation for Flow and Transport

In this section, we shall consider the discontinuous Galerkin finite element formulation of the flow coupled with the transport. Let \(\mathcal {T}_h\) be the shape-regular triangulation by a family of partitions of \(\text{\O }\) into d-simplices \(T\), \(h_T\) denote the diameter of T and \(h = \max _{T \in \mathcal {T}_h} h_T\). Also we denote by \({\mathcal {E}_h}\) the set of all edges, and by \({\mathcal {E}^{o}_h}\) and \({\mathcal {E}^{\partial }_h}\) the collection of all interior and boundary edges, respectively.

We shall also introduce standard tools such as jumps and averages of scalar and vector valued functions across the edges of \(\mathcal {T}_h\). Let e be an interior edges shared by two elements \(T^\pm \). We define the unit normal vectors \(\textbf{n}^\pm \) on e pointing exterior to \(T^\pm \), respectively. For a function \(\phi \) that is piecewise smooth on \(\mathcal {T}_h\), with \(\phi ^\pm = \phi |_{T^\pm }\), we define

$$\begin{aligned} \{\!\{\phi \}\!\} = \frac{1}{2} (\phi ^+ + \phi ^-) \quad \text{ and } \quad [\![\phi ]\!] = \phi ^+ \textbf{n}^+ + \phi ^-\textbf{n}^- \quad \forall e \in \mathcal {E}_h^o, \end{aligned}$$
(16)

where \(\mathcal {E}_h^o\) is the set of interior edges e. For a vector-valued function \(\varvec{\tau }\), piecewise smooth on \(\mathcal {T}_h\), with \(\varvec{\tau }^\pm = \varvec{\tau }|_{T^\pm }\), we define

$$\begin{aligned} \{\!\{\varvec{\tau }\}\!\} = \frac{1}{2} (\varvec{\tau }^+ + \varvec{\tau }^-) \quad \text{ and } \quad [\![\varvec{\tau } ]\!] = \varvec{\tau }^+ \textbf{n}^+ + \varvec{\tau }^-\textbf{n}^- \quad \forall e \in \mathcal {E}_h^o. \end{aligned}$$
(17)

For a set of boundary edges \(e \in \mathcal {E}_h^\partial \), let

$$\begin{aligned} [\![\phi ]\!] = \phi \textbf{n}, \quad \text{ and } \quad \{\!\{\varvec{\tau }\}\!\} = \varvec{\tau }, \quad \forall e \in \mathcal {E}_h^\partial . \end{aligned}$$
(18)

The space \(H^{s}(\mathcal {T}_h)\) \((s\in \mathbb {R})\) is the set of element-wise \(H^{s}\) functions on \(\mathcal {T}_h\) with \(s \ge 1\), and \(L^{2}({\mathcal {E}_h})\) refers to the set of functions whose traces on the elements of \({\mathcal {E}_h}\) are square integrable. Let \(\mathbb {P}_k(T)\) denote the space of polynomials of degree at most k on T. Define the space of piecewise discontinuous polynomials of degree k by

$$\begin{aligned} V_{h,k}:= \left\{ p \in L^2(\Omega ) | \ p_{|_{T}} \in \mathbb {P}_k(T), \ \forall T\in \mathcal {T}_h \right\} . \end{aligned}$$
(19)

We also use the following notations:

$$\begin{aligned} (v,w)&:=\displaystyle \sum _{T\in \mathcal {T}_h} \int _{T} v\, w dx \qquad \forall \,\, v ,w \in L^{2} (\mathcal {T}_h), \\ \langle v, w\rangle _{{\mathcal {E}_h}}&:=\displaystyle \sum _{e\in {\mathcal {E}_h}} \int _{e} v\, w \,ds \qquad \forall \, v, w \in L^{2}({\mathcal {E}_h}). \end{aligned}$$

3.1 DG Formulation for the Flow and the Concept of the Local Conservation

In this section, we use \(V_{h,k_p}\) as the DG space for the pressure approximation and present the DG formulation for the flow equation:

$$\begin{aligned} \textbf{u}&= -\kappa \nabla p, \quad \text{ in } \Omega , \end{aligned}$$
(20a)
$$\begin{aligned} \nabla \cdot \textbf{u}&= f, \quad \text{ in } \Omega , \end{aligned}$$
(20b)

which is subject to the boundary conditions (5). The interior penalty DG formulation [27, 28] for (20) is then given as: Find \(P \in V_{h,k_p}\) such that

$$\begin{aligned} \begin{aligned}&\quad (\kappa \nabla P, \nabla w) - \langle \{\!\{\kappa \nabla P\}\!\}, [\![w ]\!] \rangle _{\mathcal {E}_h} + \langle \sigma [\![P ]\!], [\![w ]\!] \rangle _{\mathcal {E}_h^o} + \langle \sigma (P-g_D), w \rangle _{\Gamma _D} \\&\quad + \theta _f \langle \{\!\{\kappa \nabla w\}\!\}, [\![P ]\!] \rangle _{\mathcal {E}_h^o} +\theta _f \langle \kappa \nabla w \cdot \textbf{n}, (P -g_D) \rangle _{\Gamma _D} \\&= (f,w)-\langle g_N\cdot \textbf{n},w\rangle _{\Gamma _N}, \quad \forall w \in V_{h,k_p}, \end{aligned} \end{aligned}$$
(21)

where \(\sigma \) is the penalty parameter and it is given as \(\sigma = O(1/h)\). Note that the parameter \(\theta _f\) determines the type of DG, namely, \(\theta _f = 0\) for IIPG, \(\theta _f = -1\) for SIPG and \(\theta _f = 1\) for NIPG [29]. We shall now present the numerical flux, which is locally conservative of degree \(k_p\).

  1. 1.

    For all \(T\in \mathcal {T}_h\) and all \(\varvec{r}_h\in [\mathbb {P}_{k_p-1}(T)]^d\)

    $$\begin{aligned} (\textbf{U},\textbf{r}_h)_T=-(\kappa \nabla P, \textbf{r}_h)_T-\theta _f \langle \{\!\{\kappa \textbf{r}_h\}\!\}, [\![P ]\!] \rangle _{\mathcal {E}_h^o\cap \partial T}-\theta _f \langle \kappa \textbf{r}_h \cdot \textbf{n}, (P -g_D) \rangle _{\Gamma _D\cap \partial T} \end{aligned}$$
    (22)
  2. 2.

    For all \(e\in \mathcal {E}_h\):

    $$\begin{aligned} \mathbf{{U}}&= -\{\!\{\kappa \nabla P\}\!\} + \sigma [\![P ]\!], \quad \text{ on } e,~\forall e \in \mathcal {E}_h^o, \end{aligned}$$
    (23a)
    $$\begin{aligned} \mathbf{{U}}\cdot \textbf{n}&= g_N, \quad \text{ on } e, ~\forall e \in \Gamma _N, \end{aligned}$$
    (23b)
    $$\begin{aligned} \mathbf{{U}}\cdot \textbf{n}&= -(\kappa \nabla P) \cdot \textbf{n}+ \sigma (P - g_D),~ \text{ on } e, \quad \forall e \in \Gamma _D, \end{aligned}$$
    (23c)

The flux \(\textbf{U}\) can be shown to satisfies the following equation for each \(T \in \mathcal {T}_h\) [17]:

$$\begin{aligned} \int _T \nabla \cdot \mathbf{{U}} w \, dx = \int _T f w \, dx, \quad \forall w \in V_{h,k_p}. \end{aligned}$$
(24)

We can view this identity as a stronger version of the local conservation since the standard local conservation is the case when the equation (24) holds for w being the piecewise constant function. Furthermore, if \(k_p\) is replaced by \(k_c\), then it has been discussed as the compatibility condition in [12], which will be discussed in more details in § 4.1 below. Thus, we are motivated to introduce this condition as a definition, i.e., the local conservation of degree k:

Definition 1

The flux \(\textbf{U}\) is said to be locally conservative of degree k with respect to the triangulation \(\mathcal {T}_h\) if and only if for all \(T \in \mathcal {T}_h\), it holds that

$$\begin{aligned} \int _T \nabla \cdot \textbf{U}\, w \, dx = \int _T f\, w \, dx, \quad \forall w \in \mathbb {P}_{k}(T). \end{aligned}$$
(25)

In § 4, we discuss the importance of the local conservation, which include \(L^2\) norm stability, zeroth order accuracy, positivity and maximum principle preserving. We remark that if \(\nabla \cdot \textbf{U}= f\), i.e., strong conservation holds, then such a local conservation is necessarily true.

3.2 DG Formulation for the Transport

In this section, we present the DG formulation for transport, primarily based on the work of Brezzi, Marini, and Süli [21] for the hyperbolic part of the transport. The elliptic part follows the standard interior penalty method by Wheeler [27], similar to the flow case.

In our discussion, we shall assume that the mesh is sufficiently small so that

$$\begin{aligned} \textbf{U}\cdot \textbf{n}_e|_e \text{ does } \text{ not } \text{ change } \text{ its } \text{ sign } \text{ for } \text{ all } e \in \mathcal {E}_h, \end{aligned}$$
(26)

where \(\textbf{n}_e\) is the normal to the edge e. This is crucial to establish the relationship between Lesaint-Raviart DG [30] and Brezzi-Marini-Süli DG. Under this assumption, for any given edge \(e \in \mathcal {E}_h^o\), which is the common edge of two triangles \(T_1\) and \(T_2\), we can determine which triangle is upstream triangle \(T^-\) and which is the downstream triangle \(T^+\). Specifically, if \(\textbf{U}\cdot \textbf{n}^1 \ge 0\), then \(T_1=T^-\) is the upstream triangle, and \(T_2=T^+\) is the downstream triangle. Otherwise, we denote \(T_1 = T^+\) and \(T_2 = T^-\). For \(e \in \mathcal {E}_h^\partial \), if \(e \in \Gamma _-\), then \(T = T^+\) while if \(e \in \Gamma _+\), then \(T = T^-\).

We shall consider the transport equation (7) and boundary condition (9) with \(\textbf{u}\) replaced by \(\textbf{U}\), i.e.,

$$\begin{aligned} \partial _t c + \nabla \cdot ( \textbf{U}c - D \nabla c) = f c^*, \quad \text{ in } \Omega \times (0,\mathbb {T}], \end{aligned}$$
(27)

subject to the boundary conditions

$$\begin{aligned} (c\textbf{U}- D\nabla c) \cdot \textbf{n}&= c_\textrm{I} \textbf{U}\cdot \textbf{n}, \quad \Gamma _\textrm{I} \times (0,\mathbb {T}] \end{aligned}$$
(28a)
$$\begin{aligned} D\nabla c \cdot \textbf{n}&= 0, \quad \Gamma _\textrm{O} \times (0,\mathbb {T}]. \end{aligned}$$
(28b)

By applying a simple Euler time discretization and Brezzi-Marini-Süli DG to (27), we have the following Euler-DG formulation: Given the old time level solution \(C^\textrm{old}\), find \(C \in V_{h,k_c}\) such that

$$\begin{aligned} \begin{aligned}&\gamma (C, w) - (\mathbf{{U}} C - D \nabla C, \nabla w) + \left\langle \left( \{\!\{C \mathbf{{U}}\}\!\} + c_e [\![C ]\!] - \{\!\{D\nabla C\}\!\} \right) , [\![w ]\!] \right\rangle _{\mathcal {E}_h^o} \\&+ \theta _c \langle \{\!\{D\nabla w\}\!\}, [\![C ]\!] \rangle _{\mathcal {E}_h^o} + \langle c_\textrm{I} \mathbf{{U}}\cdot \textbf{n}, w\rangle _{\Gamma _\textrm{I}} + \langle C\mathbf{{U}}\cdot \textbf{n}, w \rangle _{\Gamma _\textrm{O}} + \langle \sigma _D [\![C ]\!], [\![w ]\!] \rangle _{\mathcal {E}_h^o} \\&= (fC^*, w) + (g,w), \qquad \forall w \in V_{h,k_c}, \end{aligned} \end{aligned}$$
(29)

where \(g = \gamma C^\textrm{old}\) with \(\gamma = \dfrac{1}{\Delta t}\), \(c_e = |\textbf{U}\cdot \textbf{n}|/2\), the jump stabilized term, as discussed in [21], and the parameter \(\theta _c\) determines the type of DG scheme for the diffusion part of the transport, i.e., for \(\theta _c = 0\), it gives IIPG, while \(\theta _c = -1\) and \(\theta _c = 1\) give SIPG and NIPG, respectively. \(\sigma _D\) is the penalty parameter for the diffusive term. Note that \(\sigma _D = 0\) if \(D = 0\). In particular, for the pure hyperbolic case \(D = 0\), the equation (30) reduces to

$$\begin{aligned} \begin{aligned}&\gamma (C, w) - (\mathbf{{U}} C, \nabla w) + \left\langle \left( \{\!\{C \mathbf{{U}}\}\!\} + c_e [\![C ]\!] \right) , [\![w ]\!] \right\rangle _{\mathcal {E}_h^o} \\&+ \langle c_\textrm{I} \mathbf{{U}}\cdot \textbf{n}, w\rangle _{\Gamma _\textrm{I}} + \langle C\mathbf{{U}}\cdot \textbf{n}, w \rangle _{\Gamma _O} = (fC^*, w) + (g,w), \quad \forall w \in V_{h,k_c}, \end{aligned} \end{aligned}$$
(30)

which can also be written as the following formulation:

$$\begin{aligned} \begin{aligned}&\sum _{T \in \mathcal {T}_h} \int _T \gamma C w - C (\textbf{U}\cdot \nabla w)\, dx + \sum _{e \not \subset \Gamma _-} \int _e \{\!\{\textbf{U}C\}\!\} \,[\![w ]\!] \, ds + \sum _{e\in \mathcal {E}_h^0}\int _e c_e[\![C ]\!]\,[\![w ]\!]\,ds\\&=\int _\Omega fC^* w \, dx + \int _\Omega g\,w\, dx - \sum _{e \subset \Gamma _-} \int _e (\textbf{U}\cdot \textbf{n}) c_\textrm{I} w \, ds, \quad \forall w \in V_{h,k_c}, \end{aligned} \end{aligned}$$
(31)

where \(\{\!\{\textbf{U}C\}\!\}_u=\{\!\{C \mathbf{{U}}\}\!\} + c_e [\![C ]\!]\) represents the upwind value of \(\textbf{U}C\). More precisely, it is defined as across the edge of an element over which it is evaluated. We recall the definition of the upwind value for \(\textbf{U}C\), given through

$$\begin{aligned} \{\!\{\textbf{U}C\}\!\}_u = \left\{ \begin{array}{ll} \textbf{U}C^+ & \text{ if } \textbf{U}\cdot \textbf{n}^+> 0 \\ \textbf{U}C^- & \text{ if } \textbf{U}\cdot \textbf{n}^- > 0 \\ \textbf{U}\{\!\{C\}\!\} & \text{ if } \textbf{U}\cdot \textbf{n}^\pm = 0. \end{array} \right. \end{aligned}$$
(32)

4 The Zeroth Order Accuracy, \(L^2\)-Stability, Positivity and Discrete Maximum Principle (DMP)

In this section, assuming that \(\textbf{U}\) is locally conservative of degree k, we shall establish the zeroth order accuracy discussed in [12], the \(L^2\) stability, positivity and maximum principle of the solution to transports. For simplicity and within the scope of our presentation, we shall restrict our focus to the non-diffusive transports case. Namely, we assume that the transport is given by the following linear hyperbolic equation:

$$\begin{aligned} \partial _t c + \nabla \cdot (\textbf{U}c) = fc^*, \quad \text{ in } \quad \Omega \times (0,\mathbb {T}], \end{aligned}$$
(33)

subject to

$$\begin{aligned} c = c_\textrm{I}, \quad \text{ on } \quad \Gamma _- = \{ x \in \partial \Omega : \textbf{U}\cdot \textbf{n}< 0 \}. \end{aligned}$$
(34)

4.1 The Zeroth Order Accuracy

In this section, we shall discuss the zeroth order accuracy and the compatibility condition discussed in Dawson, Sun and Wheeler [12]. Basically, the compatibility condition is the minimal requirement imposed on the flux approximation to obtain meaningful solution to the transport. The meaningfulness of the solution to the transport was found at two requirements. One is the global conservation and the other is the zeroth-order accuracy. For the schemes in this paper, the requirement of the global conservation is generally independent of how \(\textbf{U}\) is computed [12]. Thus, this does not seem to be closely related to the compatibility condition. Rather, it is related to the zeroth-order accuracy. The zeroth-order accuracy can be considered to be a weaker version of the maximum or minimum principle. Namely, if the transport scheme can not reproduce a constant solution, it means there arise spurious sources and sinks due to numerical inaccuracies. In relation to DG formulation (31) of the transport, the zeroth order accuracy is shown to hold under the assumption that the numerical flux satisfies the following compatibility condition [12]:

$$\begin{aligned} - (\mathbf{{U}}, \nabla w)_\Omega + \langle \mathbf{{U}}, [\![w ]\!]\rangle _{\mathcal {E}_h^o} + \langle \mathbf{{U}}\cdot \textbf{n}, w \rangle _{\partial \Omega } = (f,w)_{\Omega }, \quad \forall w \in V_{h,k_c}. \end{aligned}$$
(35)

Note that this is obtained by setting \(C=C^*=c_\textrm{I}=c^0\) is a constant in the equation (30) and it is equivalent to the following statement, i.e., for all \(T \in \mathcal {T}_h\), it holds that

$$\begin{aligned} \int _T \nabla \cdot \textbf{U}\, w \, dx = \int _T f \, w \, dx, \quad \forall w \in V_{h,k_c}. \end{aligned}$$
(36)

We observe that the compatibility condition is the local conservation of degree \(k_c\). We remark that in the orginal work in [12], the flux formulation is introduced so that it satisfies the conservation of degree \(k_c\) only for the IIPG, i.e., \(\theta _f = 0\). On the other hand, the flux \(\textbf{U}\) presented in (23) allows for the conservation of degree k for general case. This observation is summarized in the following theorem:

Theorem 2

For \(k_c \ge 0\), the compatibility condition or the local conservation of degree \(k = k_c\) can be achieved by using \(k_p \ge k_c\) for the flow equation. This leads to the zeroth order accuracy for all \(\theta _f = -1, 0, 1\).

Proof

We recall that the flux \(\textbf{U}\) satisfies the equation (23). Thus, in order to obtain the local conservation of degree \(k_c\), it is clear that we must use \(k_p \ge k_c\). For \(k_c \ge 0\), the local conservation of degree \(k_c\) can be achieved, which leads to the zeroth order accuracy. This completes the proof. \(\square \)

In the next subsection, we shall consider two technical tools. The first one is the equivalence relationship between the Lesaint-Raviart DG method and the BMS DG method for the hyperbolic equation (33). The second one is the relationship between the Lesaint-Raviart DG method and the characteristic method along the streamline. These will play a crucial role to establish the main results in this paper.

4.2 The Lesaint-Raviart DG Method and Its Equivalence with the BMS-DG Scheme

In this section, we shall introduce the Lesaint-Raviart DG formulation for the equation (33) and show that it is equivalent to the BMS-DG formulation.

We note that similar to the streamline diffusion methods [12, 31], the Lesaint-Raviart DG formulation is based on the following reformulation of (33):

$$\begin{aligned} \partial _t c+ \textbf{U}\cdot \nabla c + (\nabla \cdot \textbf{U})c = fc^*. \end{aligned}$$
(37)

After time discretization by Euler’s method, the Lesaint-Raviart formulation is designed using the discontinuous Galerkin finite element: Find \(c_h \in V_{h,k_c}\) such that \(c_h = c_\textrm{I}\) on \(\Gamma _-\) and satisfies

$$\begin{aligned} \begin{aligned}&\sum _{T \in \mathcal {T}_h} \int _T (\textbf{U}\cdot \nabla c_h)w_h + (\nabla \cdot \textbf{U}) c_h w_h + \gamma c_h w_h \, dx \\&- \sum _{T \in \mathcal {T}_h} \int _{\Gamma _-^{\circ }(T)}(c_h^+ - c_h^-) w_h^+ (\textbf{U}\cdot \varvec{n}^+) \, ds + \sum _{e\in \Gamma _-}\int _e c_h |\textbf{U}\cdot \textbf{n}| w_h \, ds \\&= \sum _{T \in \mathcal {T}_h} \int _T (fc^* + g) w_h\, dx + \sum _{e\in \Gamma _-}\int _e c_\textrm{I} |\textbf{U}\cdot \textbf{n}|w_h\, ds, \quad \forall w_h \in V_{h,k_c}, \end{aligned} \end{aligned}$$
(38)

where \(g=\gamma c_h^{old}\) with \(\gamma =\frac{1}{\Delta t}\), \(\Gamma _-^{\circ }(T)\) represents the interior edge with \(\textbf{U}\cdot \textbf{n}<0\) and \(u^\pm = \lim \limits _{\epsilon \rightarrow 0^+} u(\varvec{x} \pm \epsilon \textbf{U})\). The following lemma basically establishes the equivalence relationship between the BMS-DG method and Lesaint-Raviart DG method.

Lemma 1

It holds true that

$$\begin{aligned} \begin{aligned}&\sum _{T \in \mathcal {T}_h} \int _{\partial T} c_h w_h (\textbf{U}\cdot \varvec{n})\, ds - \sum _{T \in \mathcal {T}_h} \int _{\Gamma _-^{\circ }(T)} (c_h^+ - c_h^-) w_h^+ (\textbf{U}\cdot \varvec{n}^+) \, ds\\&-\int _{\Gamma _-} c_h\textbf{U}\cdot \textbf{n}w_h \, ds = \sum _{e \not \subset \Gamma ^-} \int _e \{\!\{Uc_h\}\!\} \, [\![w_h ]\!] \,ds + \sum _{e \in \mathcal {E}_h^o}\int _e \frac{|\textbf{U}\cdot \varvec{n}|}{2} [\![c_h ]\!] \, [\![w_h ]\!] \, ds. \end{aligned} \end{aligned}$$
(39)

Proof

It is well known that [32]

$$\begin{aligned} \sum _{T \in \mathcal {T}_h} \int _{\partial T} (\textbf{U}\cdot \varvec{n})c_h w_h \, ds = \sum _{e \in \mathcal {E}_h} \int _e \{\!\{\textbf{U}c_h\}\!\}[\![w_h ]\!] \, ds + \sum _{e \in \mathcal {E}_h^o} \int _e [\![\textbf{U}c_h ]\!] \{\!\{w_h\}\!\}\, ds. \end{aligned}$$
(40)

Thus, we have that

$$\begin{aligned} \begin{aligned}&\sum _{T \in \mathcal {T}_h} \int _{\partial T} c_h w_h (\textbf{U}\cdot \varvec{n})\, ds - \sum _{T \in \mathcal {T}_h} \int _{\Gamma _-^{\circ }(T)} (c_h^+ - c_h^-) w_h^+ (\textbf{U}\cdot \varvec{n}^+) \, ds -\int _{\Gamma _-} c_h\textbf{U}\cdot \textbf{n}w_h \, ds \\&= \sum _{e \in \mathcal {E}_h} \int _e \{\!\{\textbf{U}c_h\}\!\}[\![w_h ]\!] \, ds + \sum _{e \in \mathcal {E}_h^o} \int _e [\![\textbf{U}c_h ]\!] \{\!\{w_h\}\!\}\, ds-\int _{\Gamma _-} c_h\textbf{U}\cdot \textbf{n}w_h \, ds\\&\quad - \sum _{T \in \mathcal {T}_h} \int _{\Gamma _-^{\circ }(T)} (c_h^+ - c_h^-) w_h^+ (\textbf{U}\cdot \varvec{n}^+) \, ds. \end{aligned} \end{aligned}$$

Since \([\![\phi ]\!] = \phi \varvec{n}\) and \(\{\!\{\varvec{\tau }\}\!\} = \varvec{\tau }\) on \(e \in \mathcal {E}_h^\partial \), we see that

$$\begin{aligned} \sum _{e \in \mathcal {E}_h} \int _e\{\!\{\textbf{U}c_h\}\!\} [\![w_h ]\!] \,ds = \sum _{e \notin \Gamma _-} \int _e\{\!\{\textbf{U}c_h\}\!\} [\![w_h ]\!] \,ds + \sum _{e \in \Gamma _-}\int _e (\textbf{U}\cdot \varvec{n} ) gw_h \, ds. \end{aligned}$$
(41)

Thus, we only need to show that

$$\begin{aligned} \begin{aligned}&\sum _{e \in \mathcal {E}_h^o} \int _e [\![\textbf{U}c_h ]\!] \{\!\{w_h\}\!\} \, ds - \sum _{T \in \mathcal {T}_h} \int _{\Gamma _-^{\circ }(T)} (c_h^+ - c_h^-) w_h^+ (\textbf{U}\cdot \varvec{n}^+) \, ds \\&= \sum _{e \in \mathcal {E}_h^o} \int _e \frac{|\textbf{U}\cdot \varvec{n}|}{2} [\![c_h ]\!]\cdot [\![w_h ]\!]\, ds. \end{aligned} \end{aligned}$$
(42)

For any given \(e \in \mathcal {E}_h^o\), we see that

$$\begin{aligned} & \quad [\![\textbf{U}c_h ]\!]\{\!\{w_h\}\!\} - (c_h^+ - c_h^-)w_h^+ \textbf{U}\cdot \textbf{n}^+ \\ & =( \textbf{U}c_h^+ \cdot \textbf{n}^+ + \textbf{U}c_h^- \cdot \textbf{n}^- ) \frac{w_h^+ + w_h^-}{2} - (c_h^+ - c_h^-) w_h^+ \textbf{U}\cdot \varvec{n}^+ \\ & = -\frac{1}{2} \textbf{U}c_h^+w_h^+ \varvec{n}^+ + \frac{1}{2} \textbf{U}c_h^+w_h^- \varvec{n}^+ -\frac{1}{2} \textbf{U}c_h^-w_h^+ \varvec{n}^- + \frac{1}{2} \textbf{U}c_h^-w_h^- \varvec{n}^- \\ & = \frac{|\textbf{U}\cdot \varvec{n}|}{2} [\![c_h ]\!] \cdot [\![w_h ]\!]. \end{aligned}$$

This completes the proof. \(\square \)

By using the integral by parts for the first term in (38), we can easily find that the Lemma 1 shows the equivalence between the BMS-DG scheme [21] and Lesaint-Raviart DG scheme [20]. Due to the equivalence relationship, we can conclude that \(C = c_h\).

4.3 The Relation between the Lesaint-Raviart DG Method and the Characteristic Method and Relevant Results

In this section, we shall investigate the relationship between the characteristic methods and the Lesaint-Raviart DG, to solve the non-divergence form of equation (37), or (33). This is crucial to prove the positivity and maximum principle of the BMS DG formulation. We first introduce an instrumental lemma.

Lemma 2

Assume that the flux satisfies the local conservation of degree \(k\ge 2k_c\). Then the system (38) reduces to the following:

$$\begin{aligned} B(C, w_h) = F(w_h), \quad \forall w_h \in V_{h,k_c}, \end{aligned}$$
(43)

where

$$\begin{aligned} \begin{aligned} B(C, w_h):=&\sum _{T \in \mathcal {T}_h} \int _T (\textbf{U}\cdot \nabla C + f_{_+} C + \gamma C) w_h \, dx \\&\,\, + \sum _{e \in \mathcal {E}_h^o} \int _e [\![C ]\!]\textbf{n}^+ w_h^+ |\textbf{U}\cdot \textbf{n}|\, ds + \sum _{e \in \Gamma _-} \int _e C |\textbf{U}\cdot \textbf{n}| w_h\, ds \nonumber \\ F(w_h):=&\int _\Omega f_{_+} \widetilde{c} w_h \, dx + \sum _{e \in \Gamma _-} \int _e c_\textrm{I} |\textbf{U}\cdot \textbf{n}| w_h\, ds + \int _\Omega g w_h \, ds, \end{aligned} \end{aligned}$$

where \(f_{_+}\) is the source and \(g = \gamma C^\textrm{old}\) with \(\gamma = \frac{1}{\Delta t}\).

Proof

Since \(\textbf{U}\) is locally conservative with the degree \(k\ge 2k_c\), we get

$$\begin{aligned} \int _\Omega \nabla \cdot \textbf{U}C w_h \, dx = \int _\Omega f C w_h \, dx, \quad \forall C, w_h \in V_{h,k_c}. \end{aligned}$$
(44)

By using the fact that \(c^* = C\) for \(f<0\), we can conclude that \(B(C,w_h)=F(w_h)\). \(\square \)

The associated norm is given as follows:

$$\begin{aligned} \Vert w\Vert _h^2 = \Vert w\Vert _{0,\Omega }^2 + \sum _{e \in \mathcal {E}_h^o} \int _e [\![w ]\!]^2 |\textbf{U}\cdot \textbf{n}| \, ds + \sum _{e \in \Gamma _-} \int _{e} w^2 |\textbf{n}\cdot \textbf{U}| \, ds, \quad \forall w \in V_{h,k_c}. \end{aligned}$$
(45)

We note that the bilinear form B satisfies the coercivity with respect to the above energy norm, i.e., \(\Vert \cdot \Vert _h\) [20]. The BMS DG can also be shown to be stable with respect to \(\Vert \cdot \Vert _h\) [21].

We shall now consider the Characteristic method following [33, 34]. We introduce a parameter \(\eta \), i.e., the pseudo time step size and denote \(S(x,t,\tau )\) the solution of differential system of characteristics:

$$\begin{aligned} \frac{dS}{d\tau } = \textbf{U}(S) \quad \text{ subject } \text{ to } S(x,t,t) = x. \end{aligned}$$
(46)

We note that since \(\textbf{U}\in W^{1,\infty }\), the Cauchy-Lipschitz theorem [35] leads to the unique existence of the solution. We shall denote the characteristic feet of x by \(X^\eta (x)\), i.e.,

$$\begin{aligned} X^\eta (x) = S(x,t,t-\eta ), \quad \forall \eta \in \mathrm{I\! R} . \end{aligned}$$
(47)

Note that \(X^\eta (x)\) is the position of x at the previous time following the velocity \(\textbf{U}\) for \(\eta > 0\) i.e., the upstream position of x for \(\eta > 0\). Under the local conservation of degree \(k = 2k_c\), the variational formulation of characteristic method is given by finding \(c^\eta \in L^2(\Omega )\) such that

$$\begin{aligned} B_\eta (c^\eta ,w) = F_\eta (w), \quad \forall w \in L^2(\Omega ), \end{aligned}$$
(48)

where

$$\begin{aligned} \begin{aligned} B_\eta (c,w):=&\frac{1}{\eta } \int _{\Omega } c w \,dx - \frac{1}{\eta } \int _{\Omega _1} c(X^\eta (x)) w \, dx + \int _\Omega (f_{_+}c + \gamma c) w \, dx \\ F_\eta (w):=&\int _\Omega f_{_+} \widetilde{c} w \, dx + \frac{1}{\eta } \int _{\Omega _2} c_\textrm{I} w \, dx + \int _\Omega g w\,dx, \end{aligned} \end{aligned}$$

with \(\Omega _1 \cup \Omega _2 = \Omega \) being such that

$$\begin{aligned} \Omega _{1} = \{x \in \Omega : X^\eta (x) \in \Omega \} \quad \text{ and } \quad \Omega _{2} = \{x \in \Omega : X^\eta (x) \notin \Omega \}. \end{aligned}$$

We now consider to solve the equation (48) using DG with the approximation space given by \(V_{h,k_c}\). The discrete problem can then be read as to find \(C^\eta \in V_{h,k_c}\) such that

$$\begin{aligned} B_\eta (C^\eta ,w_h) = F_\eta (w_h), \quad \forall w_h \in V_{h,k_c}. \end{aligned}$$
(49)

To investigate the well-posedness of the equation (49), the special energy norm denoted by \(\Vert \cdot \Vert _{h,\eta }\) has been introduced in [22], i.e.,

$$\begin{aligned} \begin{aligned}&\Vert w\Vert _{h,\eta }^2:= \int _{\Omega } w^2 \, dx + \frac{1}{\eta } \int _{\Omega _2} w^2 (x) \, dx + \frac{1}{\eta } \int _{\Omega _1} \left( w (x) - w (X^\eta (x)) \right) ^2 dx \\&\quad \quad \qquad +\int _{\Omega _3} \frac{w^2 (X^\eta (x))}{\eta } \, dx, \quad \forall w \in V_{h,k_c}. \end{aligned} \end{aligned}$$
(50)

where \(\Omega _3 = X^{-\eta }(\Omega )\backslash \Omega \). The bilinear form \(B_\eta \) is shown to be coercive with respect to the energy norm \(\Vert \cdot \Vert _{h,\eta }\) and thus, the well-posedness was established in [22]. Most importantly, the following results were established in [22]

Theorem 3

Assume that \(\textbf{U}\in W^{1,\infty }(\Omega )\). Then

$$\begin{aligned} \begin{aligned} \lim _{\eta \rightarrow 0} B_\eta (u,v)&= B(u,v), \quad \forall u, v \in V_{h,k_c}, \\ \lim _{\eta \rightarrow 0} F_\eta (v)&= F(v), \quad \forall v \in V_{h,k_c}, \end{aligned} \end{aligned}$$
(51)

and

$$\begin{aligned} \lim _{\eta \rightarrow 0} \Vert u\Vert _{h,\eta } = \Vert u\Vert _h, \quad \forall u \in V_{h,k_c}. \end{aligned}$$
(52)

The natural consequence of this theorem is that \(C_\eta \) converges to C as \(\eta \rightarrow 0\). Namely, we have

$$\begin{aligned} \lim _{\eta \rightarrow 0} C^\eta = C. \end{aligned}$$
(53)

We shall use this result to prove \(L^2\) norm stability, positivity and the maximum principle. For the \(L^2\) norm stability, we first introduce the weighted \(L^2\) norm, which is defined by

$$\begin{aligned} \Vert u\Vert _{L^2_\eta }=\left( \int _\Omega \left( 1+\eta f_{_+}+\eta \gamma \right) u^2\,dx\right) ^{\frac{1}{2}}. \end{aligned}$$
(54)

Theorem 4

Assume that the flux satisfies the local conservation of degree \(k\ge 2k_c\) and \(M=\max \{|c^0|, |c_\textrm{I}|,|\widetilde{c}|\}\), then the solution \(C^\eta \) to (48) satisfies the \(L^2_\eta \) stability:

$$\begin{aligned} \Vert C^\eta \Vert _{L^2_\eta }\le \Vert M\Vert _{L^2_\eta }. \end{aligned}$$
(55)

Proof

We shall first invoke the fixed point iteration to obtain \(c^\eta _h\). Set \(0<c^{\eta ,0}_h <M\) and consider the following iterates \(\{C^{\eta ,\ell }\}_{\ell = 0,1,\cdots }\) defined by the following rule:

$$\begin{aligned} \begin{aligned}&\frac{1}{\eta } \int _{\Omega } C^{\eta ,\ell +1} w_h \,dx - \frac{1}{\eta } \int _{\Omega _1} C^{\eta ,\ell }(X^\eta (x)) w_h \, dx + \int _\Omega (f_{_+} + \gamma ) C^{\eta ,\ell +1} w_h \, dx \\&= \int _\Omega f_{_+} \widetilde{c} w_h \, dx + \frac{1}{\eta } \int _{\Omega _2} c_\textrm{I} w_h \, dx + \int _\Omega g w_h\, dx. \end{aligned} \end{aligned}$$
(56)

We recall that \(C^\eta \) solves the following equation:

$$\begin{aligned} \begin{aligned}&\frac{1}{\eta } \int _{\Omega } C^{\eta } w_h \,dx - \frac{1}{\eta } \int _{\Omega _1} C^{\eta }(X^\eta (x)) w_h \, dx + \int _\Omega (f_{_+} + \gamma ) C^{\eta } w_h \, dx \\&= \int _\Omega f_{_+} \widetilde{c}w_h \, dx + \frac{1}{\eta } \int _{\Omega _2} c_\textrm{I} w_h \, dx + \int _\Omega g w_h \, dx. \end{aligned} \end{aligned}$$
(57)

By subtracting two equations, setting \(w_h = e_h^{\ell +1} = C^{\eta ,\ell +1} - C^\eta \) and multiplying \(\eta \) to both sides, we get

$$\begin{aligned} (1 + \eta \min _{x \in \Omega } (f_{_+} + \gamma ) )\int _{\Omega } |e_{h}^{\ell +1}|^2 \,dx= & \int _{\Omega _1} e_h^{\ell }(X^\eta (x)) e_h^{\ell +1} \, dx \\\le & \left( \int _{\Omega _1} |e_h^\ell (X^\eta )|^2 \, dx \right) ^{\frac{1}{2}} \left( \int _\Omega |e_h^{\ell +1}|^2 \,dx \right) ^{\frac{1}{2}}. \end{aligned}$$

Thus, we have the following inequality since \(X^\eta \) is one-to-one and \(\Omega _1 \subset \Omega \),

$$\begin{aligned} (1 + \eta \min _{x \in \Omega }(f_{_+} + \gamma )) \Vert e_{h}^{\ell +1}\Vert _{0,\Omega } \,dx \le \Vert e_h^\ell \Vert _{0,\Omega _1} \le \Vert e_h^\ell \Vert _{0,\Omega }. \end{aligned}$$
(58)

Thus, we prove the convergence of the fixed point iteration. Let

$$\begin{aligned} \widetilde{C}^{\eta ,\ell }(x)= \left\{ \begin{aligned}&C^{\eta ,\ell }(X^\eta (x)), & x\in \Omega _1\\&c_\textrm{I}, & x\in \Omega _2 \end{aligned} \right. \end{aligned}$$

Then we have

$$\begin{aligned} \begin{aligned}&\frac{1}{\eta } \int _{\Omega } C^{\eta ,\ell +1} w_h \,dx + \int _\Omega (f_{_+} + \gamma ) C^{\eta ,\ell +1} w_h \, dx \\&= \int _\Omega f_{_+} \widetilde{c} w_h \, dx + \frac{1}{\eta } \int _{\Omega } \widetilde{C}^{\eta ,\ell } w_h \, dx + \int _\Omega g w_h\, dx. \end{aligned} \end{aligned}$$
(59)

Take \(w_h=C^{\eta ,\ell +1}\) in the above equation, we get

$$\begin{aligned} \begin{aligned}&\quad \frac{1}{\eta } \int _{\Omega } (C^{\eta ,\ell +1})^2 \,dx + \int _\Omega (f_{_+} + \gamma ) (C^{\eta ,\ell +1})^2 \, dx \\&= \int _\Omega f_{_+} \widetilde{c} C^{\eta ,\ell +1} \, dx + \frac{1}{\eta } \int _{\Omega } \widetilde{c}_h^{\eta ,\ell } C^{\eta ,\ell +1} \, dx + \int _\Omega g C^{\eta ,\ell +1}\, dx\\&\le \frac{1}{2}\int _\Omega f_{_+}|\widetilde{c}|^2\, dx +\frac{1}{2}\int _\Omega f_{_+}|C^{\eta ,\ell +1}|^2\, dx + \frac{1}{2\eta }\int _\Omega |\widetilde{C}^{\eta ,\ell }|^2\, dx + \frac{1}{2\eta } \int _\Omega |C^{\eta ,\ell +1}|^2\, dx\\&\quad + \frac{1}{2}\int _\Omega \gamma |C^{old}|^2\,dx + \frac{1}{2}\int _\Omega \gamma |C^{\eta ,\ell +1}|^2\, dx \end{aligned} \end{aligned}$$
(60)

by using the Cauchy-Schwarz inequality and the Young’s equation. Therefore,

$$\begin{aligned} \begin{aligned}&\quad \int _\Omega \left( 1+\eta f_{_+}+\eta \gamma \right) |C^{\eta ,\ell +1}|^2\, dx\\&\le \int _\Omega \eta f_{_+}|\widetilde{c}|^2\, dx +\int _\Omega |\widetilde{C}^{\eta ,\ell }|^2\, dx+\int _\Omega \eta \gamma |C^{old}|^2\,dx\\&\le \int _\Omega \left( 1+\eta f_{_+}+\eta \gamma \right) M^2\,dx. \end{aligned} \end{aligned}$$
(61)

Thus, \(\Vert C^{\eta ,\ell +1}\Vert _{L^2_\eta }\le \Vert M\Vert _{L^2_\eta }\). By the convergence of this iterative method, we get the result \(\Vert C^{\eta }\Vert _{L^2_\eta }\le \Vert M\Vert _{L^2_\eta }\). \(\square \)

Theorem 5

Assume that the flux satisfies the local conservation of degree \(k\ge 2k_c\), and suppose that the problem (33) has the nonnegative inflow \(c_\textrm{I}\) and initial \(c^0\) condition, \(M=\max \{|c^0|, |c_\textrm{I}|, |\widetilde{c}|\}\). Then the numerical solution C obtained by BMS-DG satisfies the \(L^2\) stability.

Proof

We can easily find that \(\lim \limits _{\eta \rightarrow 0}\Vert u\Vert _{L^2_\eta }=\Vert u\Vert _{L^2}\). Thus, by combining the Theorem 3 and the equation (53), we can conclude that

$$\begin{aligned} \Vert C\Vert _{L^2} \le \Vert M\Vert _{L^2}. \end{aligned}$$
(62)

This completes the proof. \(\square \)

Next, we shall assume that \(k_c = 0\) and prove the positivity and the maximum principle.

Theorem 6

Assume that the flux satisfies the local conservation of degree \(k\ge 2k_c=0\). The solution \(C^\eta \) to (49) satisfies \(0\le C^\eta \le M\), where

$$\begin{aligned} M = \max \{|c^{0}|, |c_\textrm{I}|,|\widetilde{c}| \}. \end{aligned}$$
(63)

Proof

Consider piecewise constant function in (59), define \(w_h=1\) in T and \(w_h=0\) in others, then we have

$$\begin{aligned} \begin{aligned}&\frac{1}{\eta } \int _T C^{\eta ,\ell +1} \,dx + \int _T (f_{_+} + \gamma ) C^{\eta ,\ell +1} \, dx \\&= \int _T f_{_+} \widetilde{c} \, dx + \frac{1}{\eta } \int _{T} \widetilde{C}^{\eta ,\ell }(x) \, dx + \int _T g\, dx. \end{aligned} \end{aligned}$$
(64)

Obviously, we can get \(C^{\eta ,\ell +1}\ge 0\) by induction. Additionally, the above equation yields

$$\begin{aligned} \begin{aligned} \int _T \left( \frac{1}{\eta }+f_{_+} + \gamma \right) C^{\eta ,\ell +1}\, dx&= \int _T f_{_+} \widetilde{c} \, dx + \frac{1}{\eta } \int _{T} \widetilde{C}^{\eta ,\ell } \, dx + \int _T g\, dx \\&\le \int _T \left( \frac{1}{\eta }+f_{_+} + \gamma \right) M\,dx. \end{aligned} \end{aligned}$$
(65)

Then we have,

$$\begin{aligned} \begin{aligned} \int _T \left( \frac{1}{\eta }+f_{_+} + \gamma \right) (C^{\eta ,\ell +1}-M)\,dx\le 0. \end{aligned} \end{aligned}$$

Thus, \(C^{\eta ,\ell +1}\le M\) since \(\dfrac{1}{\eta }+f_{_+} + \gamma >0\). Using the fact that the fixed point iteration converges, we can conclude that \(0\le C^\eta \le M\). \(\square \)

Combined with the above theorem and (53), we can obtain the positivity and the discrete maximum principle.

Theorem 7

Assume that the flux satisfies the local conservation of degree \(k\ge 2k_c=0\) and suppose that the problem (33) has the nonnegative inflow \(c_\textrm{I}\) and initial condition \(c^0\), \(M=\max \{|c^0|, |c_\textrm{I},|\widetilde{c}|\}\). Then the numerical solution C obtained by BMS-DG satisfies the positivity and the discrete maximum principle.

5 Numerical Experiments

In this section, we present a simple numerical experiment that confirms our theory. We shall consider to solve the transport equation (7) with \(\textbf{u}\) governed by the Darcy’s law (4). Here we assume \(\mu (c) = 1\).

5.1 1D Case of Propagating a Concentration Front Through the Domain

We first consider the one-dimensional transport equation without the diffusion term:

$$\begin{aligned} \partial _t c + (uc)_x = fc^*, \quad 0< x < 1, \text{ with } t > 0, \end{aligned}$$
(66)

where \(f = u_x = -\pi /2 \sin (\pi x/2)\) is the sink, that is \(c^* = c\). Note that there is no source in this case. For the flow equation, we choose \(K=1\) with Dirichlet boundary condition given as \(p(0)=0\) and \(p(1)=-2/\pi \). Thus, the flow direction is from left to right, we let the inflow concentration \(c_\textrm{I}=1\) and the initial condition \(c^0=0.1\).

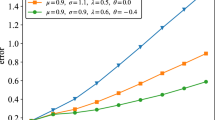
We study the behavior of the solution and the maximum principle. We discretize the interval [0, 1] with 10, 20 and 50 grid blocks, respectively. For the time step, we use \(\Delta t=0.02\) at \(T=0.5\). Use the piecewise linear function for the flow equation with penalty parameter \(\sigma =100/h\). From the first two figures in Fig. 1, we find that this method give virtually identical transport solutions, namely a traveling front two constant regions where \(c=1\) and \(c=0.1\). However, when using a piecewise linear function for the transport, we observe that the solution encounters nonphysical values, even when we use 300 points.

Fig. 1
figure 1

Concentration values at \(T=0.5\) with piecewise constant function(left) and piecewise linear function(right)

Full size image

5.2 2D Case with No External Force and No Diffusion

A simple example is the permeability block. Let \(\Omega = (0,1)^2\), and the permeability tensor \(\kappa \) is defined as a diagonal tensor defined as follows:

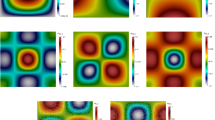
$$\begin{aligned} \begin{aligned} \varvec{\kappa } = \left\{ \begin{array}{l} \left( \begin{array}{cc} 10^{-3} & 0 \\ 0 & 10^{-3} \end{array} \right) \text{ in } \Omega _s = \left( \frac{3}{8}, \frac{5}{8} \right) \times \left( \frac{1}{4}, \frac{3}{4} \right) \\ \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \text{ elsewhere. } \end{array} \right. \end{aligned} \end{aligned}$$
(67)

The inflow boundary condition for c is given as \(c_\textrm{I} = 1 \text{ on } \Gamma _{D1} \times (0, T],\) subject to the initial condition \(c(0,x) = 0\) in \(\Omega \). The pressure boundary condition is given as \(p = 1 \text{ on } \Gamma _{D1}\), \(p = 0 \text{ on } \Gamma _{D2}\) and \(\textbf{u}\cdot \textbf{n}= 0 \text{ on } \Gamma _N\) For simplicity, we shall set \(f = D(\textbf{u}) = 0\). The block and the solution to the flow equation solved by \(DG_1\) can be seen in Fig. 2. After applying a piecewise constant function to solve the transport equation, we obtain the results depicted in Fig. 3, showcasing \(T=0.5, 1, 1.5,\) and 3 from left to right. These results adhere to the maximum principle and maintain positivity.

Fig. 2
figure 2

Left: Domain; Middle: K-block; Right: Pressure

Full size image
Fig. 3
figure 3

Concentration values at \(T=0.5, 1.0, 1.5, 3.0\) (from left to right)

Full size image

5.3 2D Case with External Force for Injection and Extraction

We now consider the nonzero external force case. Let \(\Omega = (0,1)^2\). The diagonal entry for the permeability \(\varvec{\kappa }\) is defined by:

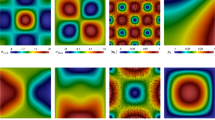
$$\begin{aligned} \varvec{\kappa } = \left\{ \begin{array}{l} \left( \begin{array}{cc} 10^{-3} & 0 \\ 0 & 10^{-3} \end{array} \right) \text{ for } x \ge 0.5 \\ \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \text{ elsewhere. } \end{array} \right. \end{aligned}$$
(68)

The fluid is injected at the corner (0, 0) with the injection rate \(f^+=100\), and it is extracted at the corner (1, 1) with the extraction rate \(f^-=-100\). Using the piecewise linear function for the flow equation and the piecewise constant function for the transport equation, we set \(\Delta t=h=0.01\). In Fig. 4, we can see that the fluid smears into the low permeability zone and towards the extraction point, results in a physical values. If we use the piecewise linear function for transport equation, solutions greater than 1 will occur.

Fig. 4
figure 4

Concentration values at \(T=0, 4, 6, 10\) with injection and extraction. The first row used the piecewise constant function and the second row used the piecewise linear function

Full size image

6 Conclusions

In this paper, we introduce the new concept of the locally conservative flux, i.e., the local conservation of degree \(k \ge 0\). This can be interpreted as the intermediate local conservation between the standard local conservation and the strong conservation. Under this condition, we prove the \(L^2\)-stability for the transport equation. Besides, we show how the positivity and maximum principle can be obtained when the piecewise constant function is used for approximating the transport. This resolves the long standing open question. Finally, several numerical experiments are carried out to verify the theoretical results.