Skip to main content
Springer Nature Link
Log in

Efficient Structure-Preserving Scheme for the Space Fractional Allen–Cahn Equation with Logarithmic Flory–Huggins Potential

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

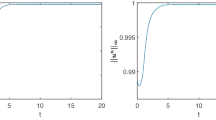
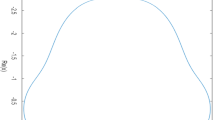
Abstract

In this paper, a numerical method is proposed for solving the space fractional Allen–Cahn equation with logarithmic Flory–Huggins potential. Due to the strong nonlinearity of potential function and singularity of logarithmic term, how to constructed an effective scheme that preserves both the unconditional discrete maximum principle and unconditional original energy stability is a great challenge for this problem. To overcome these difficulties, the stabilized method is applied to construct a structure-preserving scheme, where the weighted and shifted Grünwald difference formula is used to approximate the Riesz fractional derivative. The advantages of this method are that the nonlinear logarithmic term is explicitly treated, the proposed scheme is linear and easy to implement and it preserves the unconditional original energy stability. Then, for any time step, the unique solvability of scheme, discrete maximum principle preserving and original energy stability are all rigorously proved. Moreover, the detailed error estimate in maximum norm is given. In addition, adaptive time-stepping algorithm is used to improve computational efficiency in long time simulations. In numerical experiments, the effects of fractional order \(\alpha \) on the phase change process are also studied. The numerical results verify the effectiveness of the proposed algorithms and the correctness of the theoretical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability

All data generated or analysed during this study are included in this article.

References

  1. Cahn, J.W., Hilliard, J.E.: Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28(2), 258–267 (1958)

    MATH  Google Scholar 

  2. Xu, C., Prince, J.L.: Snakes, shapes, and gradient vector flow. IEEE Trans. Image Process. 7(3), 359–369 (1998)

    MathSciNet  MATH  Google Scholar 

  3. Liu, C., Shen, J.: A phase field model for the mixture of two incompressible fluids and its approximation by a Fourier-spectral method. Phys. D 179(3–4), 211–228 (2003)

    MathSciNet  MATH  Google Scholar 

  4. Anderson, D.M., McFadden, G.B., Wheeler, A.A.: Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 30(1), 139–165 (1998)

    MathSciNet  MATH  Google Scholar 

  5. Du, Q., Liu, C., Wang, X.: A phase field approach in the numerical study of the elastic bending energy for vesicle membranes. J. Comput. Phys. 198(2), 450–468 (2004)

    MathSciNet  MATH  Google Scholar 

  6. Evans, L.C., Soner, H.M., Souganidis, P.E.: Phase transitions and generalized motion by mean curvature. Commun. Pure Appl. Math. 45(9), 1097–1123 (1992)

    MathSciNet  MATH  Google Scholar 

  7. Allen, S.M., Cahn, J.W.: A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27, 1085–1095 (1979)

    MATH  Google Scholar 

  8. Hou, D., Ju, L., Qiao, Z.: A linear second-order maximum bound principle-preserving BDF scheme for the Allen-Cahn equation with a general mobility. Math. Comput. 92(344), 2515–2542 (2023)

    MathSciNet  MATH  Google Scholar 

  9. Yang, X., Zhang, G.: Convergence analysis for the invariant energy quadratization (IEQ) schemes for solving the Cahn-Hilliard and Allen-Cahn equations with general nonlinear potential. J. Sci. Comput. 82, 1–28 (2020)

    MathSciNet  MATH  Google Scholar 

  10. Geng, Y., Teng, Y., Wang, Z., et al.: A deep learning method for the dynamics of classic and conservative Allen-Cahn equations based on fully-discrete operators. J. Comput. Phy. 496, 112589 (2024)

    MathSciNet  MATH  Google Scholar 

  11. Li, J., Ju, L., Cai, Y., et al.: Unconditionally maximum bound principle preserving linear schemes for the conservative Allen-Cahn equation with nonlocal constraint. J. Sci. Comput. 87, 1–32 (2021)

    MathSciNet  MATH  Google Scholar 

  12. Shen, J., Tang, T., Yang, J.: On the maximum principle preserving schemes for the generalized Allen-Cahn equation. Commun. Math. Sci. 14(6), 1517–1534 (2016)

    MathSciNet  MATH  Google Scholar 

  13. Zhang, B., Bu, W., Xiao, A.: Efficient difference method for time-space fractional diffusion equation with Robin fractional derivative boundary condition. Numer. Algorithms 88, 1965–1988 (2021)

    MathSciNet  MATH  Google Scholar 

  14. Tian, W., Zhou, H., Deng, W.: A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 84(294), 1703–1727 (2015)

    MathSciNet  MATH  Google Scholar 

  15. Yang, Y., Chen, Y., Huang, Y., et al.: Spectral collocation method for the time-fractional diffusion-wave equation and convergence analysis. Comput. Math. Appl. 73(6), 1218–1232 (2017)

    MathSciNet  MATH  Google Scholar 

  16. Yang, Y., Wang, J., Chen, Y., et al.: Compatible \(L^2\) norm convergence of variable-step L1 scheme for the time-fractional MBE model with slope selection. J. Comput. Phy. 467, 111467 (2022)

    MATH  Google Scholar 

  17. Liao, H., Tang, T., Zhou, T.: An energy stable and maximum bound preserving scheme with variable time steps for time fractional Allen-Cahn equation. SIAM J. Sci. Comput. 43(5), A3503–A3526 (2021)

    MathSciNet  MATH  Google Scholar 

  18. Huang, C., Stynes, M.: A sharp \(\alpha \)-robust \(L^\infty (H^1)\) error bound for a time-fractional Allen-Cahn problem discretised by the Alikhanov \(L2-1_\sigma \) scheme and a standard FEM. J. Sci. Comput. 91(2), 43 (2022)

    MATH  Google Scholar 

  19. Liao, H., Zhu, X., Sun, H.: Asymptotically compatible energy and dissipation law of the nonuniform \(L2-1_\sigma \) scheme for time fractional Allen-Cahn model. J. Sci. Comput. 99(2), 46 (2024)

    MathSciNet  MATH  Google Scholar 

  20. Nec, Y., Nepomnyashchy, A., Golovin, A.: Front-type solutions of fractional Allen-Cahn equation. Physica D 237(24), 3237–3251 (2008)

    MathSciNet  MATH  Google Scholar 

  21. Copetti, M.I.M., Elliott, C.M.: Numerical analysis of the Cahn-Hilliard equation with a logarithmic free energy. Numer. Math. 63, 39–65 (1992)

    MathSciNet  MATH  Google Scholar 

  22. Cherfils, L., Miranville, A., Zelik, S.: The Cahn-Hilliard equation with logarithmic potentials. Milan J. Math. 79, 561–596 (2011)

    MathSciNet  MATH  Google Scholar 

  23. Hou, T., Tang, T., Yang, J.: Numerical analysis of fully discretized Crank-Nicolson scheme for fractional-in-space Allen-Cahn equations. J. Sci. Comput. 72, 1214–1231 (2017)

    MathSciNet  MATH  Google Scholar 

  24. He, D., Pan, K., Hu, H.: A spatial fourth-order maximum principle preserving operator splitting scheme for the multi-dimensional fractional Allen-Cahn equation. Appl. Numer. Math. 151, 44–63 (2020)

    MathSciNet  MATH  Google Scholar 

  25. Chen, H., Sun, H.: A dimensional splitting exponential time differencing scheme for multidimensional fractional Allen-Cahn equations. J. Sci. Comput. 87(1), 30 (2021)

    MathSciNet  MATH  Google Scholar 

  26. Cai, Y., Sun, H., Tam, S.: Numerical study of a fast two-level strang splitting method for spatial fractional Allen-Cahn equations. J. Sci. Comput. 95(3), 71 (2023)

    MathSciNet  MATH  Google Scholar 

  27. Zhang, B., Yang, Y.: A new linearized maximum principle preserving and energy stability scheme for the space fractional Allen-Cahn equation. Numer. Algorithms 93(1), 179–202 (2023)

    MathSciNet  MATH  Google Scholar 

  28. Zhang, H., Yan, J., Qian, X., et al.: On the preserving of the maximum principle and energy stability of high-order implicit-explicit Runge-Kutta schemes for the space-fractional Allen-Cahn equation. Numer. Algorithms 88, 1309–1336 (2021)

    MathSciNet  MATH  Google Scholar 

  29. Hu, B., Zhang, W., Zhao, X.: Convergence analysis of the maximum principle preserving BDF2 scheme with variable time-steps for the space fractional Allen-Cahn equation. J. Comput. Appl. Math. 448, 115951 (2024)

    MathSciNet  MATH  Google Scholar 

  30. Chen, H., Sun, H.: Second-order maximum principle preserving Strang’s splitting schemes for anisotropic fractional Allen-Cahn equations. Numer. Algorithms 90(2), 749–771 (2022)

    MathSciNet  MATH  Google Scholar 

  31. Chen, W., Wang, C., Wang, X., et al.: Positivity-preserving, energy stable numerical schemes for the Cahn-Hilliard equation with logarithmic potential. J. Comput. Phys. X 3, 100031 (2019)

    MathSciNet  MATH  Google Scholar 

  32. Izsák, F.J., Szekeres, B.: Models of space-fractional diffusion: a critical review. Appl. Math. Lett. 71, 38–43 (2017)

    MathSciNet  MATH  Google Scholar 

  33. Qiao, Z., Zhang, Z., Tang, T.: An adaptive time-stepping strategy for the molecular beam epitaxy models. SIAM J. Sci. Comput. 33(3), 1395–1414 (2011)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China Project (No. 12261131501), the Project of Scientific Research Fund of the Hunan Provincial Science and Technology Department (No. 2023GK2029, No. 2024JC1003, No. 2024JJ1008), and “Algorithmic Research on Mathematical Common Fundamentals” Program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province of China.

Author information

Authors and Affiliations

  1. CAS AMSS-PolyU Joint Laboratory of Applied Mathematics, The Hong Kong Polytechnic University Shenzhen Research Institute, Shenzhen, 518057, China

    Biao Zhang

  2. Hunan Key Laboratory for Computation and Simulation in Science and Engineering, Xiangtan University, Xiangtan, 411105, Hunan, China

    Biao Zhang

  3. School of Mathematics and Computational Science, Xiangtan University, Xiangtan, 411105, Hunan, China

    Yin Yang

  4. National Center for Applied Mathematics in Hunan, Hunan International Scientific and Technological Innovation Cooperation Base of Computational Science, Xiangtan, 411105, Hunan, China

    Yin Yang

Authors
  1. Biao Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yin Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yin Yang.

Ethics declarations

Conflict of interest

The authors declare that they have no Conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, B., Yang, Y. Efficient Structure-Preserving Scheme for the Space Fractional Allen–Cahn Equation with Logarithmic Flory–Huggins Potential. J Sci Comput 103, 18 (2025). https://doi.org/10.1007/s10915-025-02832-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-025-02832-1

Keywords