Pointwise Error Bounds in POD Methods Without Difference Quotients

Abstract

In this paper we consider proper orthogonal decomposition (POD) methods that do not include difference quotients (DQs) of snapshots in the data set. The inclusion of DQs have been shown in the literature to be a key element in obtaining error bounds that do not degrade with the number of snapshots. More recently, the inclusion of DQs has allowed to obtain pointwise (as opposed to averaged) error bounds that decay with the same convergence rate (in terms of the POD singular values) as averaged ones. In the present paper, for POD methods not including DQs in their data set, we obtain error bounds that do not degrade with the number of snapshots if the function from where the snapshots are taken has certain degree of smoothness. Moreover, the rate of convergence is as close as that of methods including DQs as the smoothness of the function providing the snapshots allows. We do this by obtaining discrete counterparts of Agmon and interpolation inequalities in Sobolev spaces. Numerical experiments validating these estimates are also presented.

1 Introduction

There seems to be an unclosed debate on wether it is necessary or advisable to include the difference quotients (DQs) of the snapshots (or function values) in the data set in proper orthogonal decomposition (POD) methods. These allow for a remarkable dimension reduction in large-scale dynamical systems by projecting the equations onto smaller spaces spanned by the first elements of the POD basis. This basis is extracted from the data set, originally the set of snapshots, although, as mentioned, some authors include their DQs. Inclusion of these has been essential to obtain optimal error bounds [8, 12, 15, 19] for POD methods. More recently, pointwise (in time) error bounds have been proved in case DQs are added to the set of snapshots [12], or if the DQs are complemented with just one snapshot [4]. In fact, counterexamples are presented in [12] showing that if DQs are not included, pointwise projection errors degrade with the number of snapshots. However, this degradation is hard to find in many practical instances, and, at the same time, while some authors report improvement in their numerical simulations if DQs are included in the data set [8], others find just the opposite [10, 11].

The present paper does not pretend to settle the argument, but hopes to shed some light on why, in agreement with the numerical experience of some authors, it may be possible to obtain good results in practice without including DQs. In particular, we show that if a function has first derivatives (with respect to time) square-integrable in time, POD projection errors do not degrade with the number of snapshots. Furthermore, if second or higher-order derivatives are square-integrable in time, POD methods are convergent and, the higher the order of the derivatives that are square integrable, the closer to optimal the rate of convergence becomes. We do this by obtaining discrete versions of Agmon and interpolation inequalities in Sobolev spaces, which allow to bound the $L^\infty$ norm of a function in terms of the $L^2$ norm and higher-order Sobolev’s norms.

We remark that our results do not contradict previous results in the literature. On the one hand, the error bounds we prove are as close to optimal as the smoothness of the solution allows, but not optimal. On the other hand, concerning the counterexamples in [12], we notice that they require the snapshots to be multiples of the POD basis and, hence, an orthogonal set, a property that is lost if a function is smooth and the snapshots are function values taken at increasingly closer times as the number of snapshots increases, because, on the one hand, the distance between two orthogonal vectors is not smaller than their norms and, on the other hand, for a continuous function, the distance between two consecutive function values of finer and finer partitions tends to zero. In conclusion, the snapshots of the counterexamples in [12] cannot be function values of the same function at denser and denser partitions of the same time interval.

The reference [15] is the first one showing convergence results for POD methods for parabolic problems. Starting with this paper one can find several references in the literature developing the error analysis of POD methods. We mention some references that are not intended to be a complete list. In [16] the same authors of [15] provide error estimates for POD methods for nonlinear parabolic systems arising in fluid dynamics. The authors of [3] show that comparing the POD approximation with the $L^2$ projection over the reduced order space instead of the $H_0^1(\Omega )$-projection (as in [15]) DQs are not required in the set of snapshots. However, in that case, the norm of the gradient of the $L^2$-projection has to be bounded. This leads to non-optimal estimates for the truncation errors, see [12]. POD approximation errors in different norms and using different projections can also be found in [19].

The rest of the paper is as follows. In Sect. 2 we present the main results of this paper and their application to obtain pointwise error bounds in POD methods based only on snapshots. Section 3 present some numerical experiments. In Sect. 4, the auxiliary results needed to prove the main results in Sect. 2 are stated and proved, and the final section contains the conclusions.

2 Main Results

Let $\Omega$ be a bounded region in ${\mathbb {R}}^d$ with a smooth boundary or a Lipschitz polygonal boundary. We use standard notation, so that $H^s(\Omega )$ denotes the standard Sobolev space of index s. We also consider the space $H^1_0(\Omega )$ of functions vanishing on the boundary and with square integrable first derivatives. Let $T>0$ and let $u: \Omega \times [0,T] \rightarrow {\mathbb {R}}$ be a function such that its partial derivative with respect to its second argument, denoted by t henceforth, satisfies that $u\in H^m(0,T,X)$, where X denotes either $L^2(\Omega )$ or $H^1_0(\Omega )$, and

$$\begin{aligned} \left\| u\right\| _{H^m(0,T,X)} =\biggl ( \sum _{k=0}^m \frac{1}{T^{2(m-j)}}\int _0^T \bigl \Vert \partial _t^k u(\cdot ,t)\bigr \Vert _X^2\,\textrm{d}t\biggr )^{1/2} \end{aligned}$$

(1)

and $\left\| \cdot \right\| _X$ denotes the norm in X, that is $\left\| f\right\| _X=(f,f)^{1/2}$ if $X=L^2(\Omega )$ or $\left\| f\right\| _X=(\nabla f,\nabla f)^{1/2}$ if $X=H^1_0(\Omega )$. Typically, in many practical instances, u is a finite element approximation to the solution of some time-dependent partial differential equation. The factors $1/T^{2(m-j)}$ in the definition of $\left\| \cdot \right\| _{H^m(0,T,X)}$ are introduced so that the constants in the estimates that follow are scale-invariant (see e.g., [2, Chapter 4]). In what follows, if a constant is denoted with a lower case letter, this means that it is scale-invariant.

Given a positive integer $M>0$ and the corresponding time-step $\Delta t=T/M$, we consider the time levels $t_n=n\Delta t$, $n=0,\ldots ,M$, and the function values or snapshots of u

$$\begin{aligned} u^n = u(\cdot ,t_n),\qquad n=0,\ldots ,M. \end{aligned}$$

We denote by $\sigma _1\ge \ldots \ge \sigma _{J}$ the singular values and by $\varphi ^1,\ldots ,\varphi ^{J}$ the left singular vectors of the operator from ${\mathbb {R}}^{M+1}$ (endorsed with the standard Euclidean norm) which maps every vector $x=[x_1,\ldots ,x_{M+1}]^T$ to

$$\begin{aligned} Kx=\frac{1}{\sqrt{M+1}}\sum _{n=0}^M x_{n+1} u^n, \end{aligned}$$

(2)

operator which, being of finite rank, is compact. The singular values satisfy that $\lambda _k=\sigma _k^2$, for $k=1,\ldots ,J$ are the positive eigenvalues of the correlation matrix $M=\frac{1}{M+1}((u^i,u^j)_X)_{0\le i,j\le M}$. The left singular vectors, known as the POD basis, are mutually orthogonal and with unit norm in X. For $1\le r\le d$ let us denote by

$$\begin{aligned} V_r=\textrm{span}(\varphi ^1,\ldots ,\varphi ^r), \end{aligned}$$

and by $P^r_X:X\rightarrow V_r$ the orthogonal projection of X onto $V_r$. It is well-known that

$$\begin{aligned} \frac{1}{M+1}\sum _{n=0}^M \bigl \Vert u^n - P_X^r u^n\bigr \Vert _X^2 =\sum _{k>r} \sigma _k^2. \end{aligned}$$

(3)

In the present paper, the rate of decay given by the square root of the right-hand side above will be referred to as optimal (see [8]).

In many instances of interest in practice, at least when u is a finite element approximation to the solution of a dissipative partial differential equation (PDE), the singular values decay exponentially fast, so that for very small values of r (compared with the dimension of the finite element space) the right-hand side of (3) is smaller than the error of u with respect the solution of the PDE it approximates.

POD methods are Galerkin methods where the approximating spaces are the spaces $V_r$. In POD methods, one obtains values $u_r^n\in V_r$ intended to be approximations $u_r^n\approx u^n$, $n=0,\ldots , M$, and (3) is key in obtaining estimates for the errors $u_r^n-u^n$. Yet, the fact that the left hand side (3) is an average allows only for averaged estimates of the errors $u_r^n-u^n$, and one would be interested in pointwise estimates. In order to obtain them, some authors assume (without a result to support it) that the individual errors $\bigl \Vert u^n-P_X^r u^n\bigr \Vert _X$ decay with r as the square root of the right-hand side of (3) (see e.g., [9, (2.9)]).

Yet, in principle, the only rigorous pointwise estimate that one can deduce from (3) is

$$\begin{aligned} \bigl \Vert u^n - P_X^r u^n\bigr \Vert _X \le \sqrt{M+1} \biggl (\sum _{k>r} \sigma _k^2\biggr )^{\frac{1}{2}}, \qquad n=0,\ldots ,M. \end{aligned}$$

(4)

This estimate is sharp as shown in examples provided in [12], where for at least one value of n, the equality is reached. Estimate (4) degrades with the number $M+1$ of snapshots. One would expect then in practice that if M is increased while maintaining the value of r the individual errors $\bigl \Vert u^n - P_X^r u^n\bigr \Vert _X$ should increase accordingly. Yet this is not necessary the case as results in Table 1 show, with correspond to the snapshots of the quadratic FE approximation to the periodic solution of the Brusselator problem described in [7] (see also Sect. 3 below) in the case where $X=L^2(\Omega )$, $r=25$ and T is one period.

Table 1 Maximum pointwise projection error $\max _{0\le n\le M}\bigl \Vert u^n - P_X^r u^n\bigr \Vert _X$ for different values of the number of snapshots $M+1$ and u being the quadratic FE approximation to the periodic solution of the Brusselator problem described in [7], when $X=L^2(\Omega )$, $r=25$ and T is one period

The results in Table 1 are in agreement with the following result.

Theorem 2.1

Let u be bounded in $H^1(0,T,X)$. Then, for the constant $c_A$ defined in (40) below, the following bound holds:

$$\begin{aligned} \max _{0\le n\le M}\bigl \Vert u^n - P_X^r u^n\bigr \Vert _X \le c_A \biggl ({2T}\sum _{k>r} \sigma _k^2\biggr )^{\frac{1}{4}}\bigl \Vert (I-P_X^r)\partial _t u\Vert _{L^2(0,T,X)}^{\frac{1}{2}} + \biggl ({2}\sum _{k>r} \sigma _k^2\biggr )^{\frac{1}{2}}. \end{aligned}$$

If $u_0+\cdots +u_M=0$, then the second term on the right-hand side above can be omitted.

Proof

The result is a direct consequence of the case $m=1$ in estimate (73) in Theorem 4.12 below when applied to $f=u-P_X^r u$ and the identity (3) above, as we now explain. The norm $\left\| \cdot \right\| _0$ in (73) is defined in (38–39). With this norm and applying (3), we have

$$\begin{aligned} \left\| u-P_X^r u\right\| _0&=\biggl (\frac{T}{M} \sum _{n=0}^M \left\| u-P_X^r u\right\| _0^2\biggr )^\frac{1}{2} =\biggl (\frac{M+1}{M} T\sum _{k>r}\sigma _k^2\biggr )^\frac{1}{2} , \end{aligned}$$

(5)

and the proof is finished by noticing that $(M+1)/M\le 2$, for $M\ge 1$. $\square$

Observe that in the pointwise estimate in Theorem 2.1 no factor depending on M appears on the right-hand side, except, perhaps, the singular values, but if $u\in H^1(0,T,X)$ then, $\sigma _k\rightarrow \sigma _{c,k}$ as $M\rightarrow \infty$, where $\sigma _{c,1}\ge \sigma _{c,2} \ge \ldots \,$, are the singular values of the operator $K_c:L^2(0,T)\rightarrow X$ given by [16, Section 3.2]

$$\begin{aligned} K_cf=\frac{1}{T} \int _0^t f(t)u(t)\,\textrm{d}t. \end{aligned}$$

Observe also that, at worst,

$$\begin{aligned} \bigl \Vert (I-P_X^r)\partial _t u\bigr \Vert _{L^2(0,T,X)} \le \bigl \Vert \partial _t u\Vert _{L^2(0,T,X)}. \end{aligned}$$

Thus, Theorem 2.1 guarantees that pointwise projection errors do not degrade as the number of snapshots increases. Furthermore, they decay with r, although like $\left( \Sigma _{k>r} \sigma _k^2\right) ^{1/4}$, which is the square root of the optimal rate. Yet, the following result shows that pointwise projection errors decay with a rate as close to optimal as the smoothness of u allows. In the sequel we define

$$\begin{aligned} r_M=\frac{M+1}{M} \end{aligned}$$

(6)

Theorem 2.2

Let u be bounded in $H^m(0,T,X)$. Then, for the constants $c_A$ defined in  (48) and $c_m$ in Lemma 4.10 below, the following bound holds:

$$\begin{aligned} \max _{0\le n\le M} \bigl \Vert u^n - P_X^r u^n\bigr \Vert _X \le&\sqrt{2} c_Ac_m^{\frac{1}{2}} \biggl ({r_MT}\sum _{k>r} \sigma _k^2\biggr )^{\frac{1}{2}-\frac{1}{4m}}\bigl \Vert (I-P_X^r)\partial _t u\bigr \Vert _{H^{m-1}(0,T,X)}^{\frac{1}{2m}} \nonumber \\& + \biggl ({r_M}\sum _{k>r} \sigma _k^2\biggr )^{\frac{1}{2}}. \end{aligned}$$

If $u_0+\cdots +u_M=0$, then the second term on the right-hand side above can be omitted.

Proof

Similarly to Theorem 2.1, the result is a direct consequence of estimate (73) in Theorem 4.12 below applied to $f=u-P_X^r u$, the identity (3) above and (5). $\square$

The above results account for projection errors, but in the analysis of POD methods the error between the POD approximation and the snapshots, $u_r^n - u^n$ depends also on the difference quotients

$$\begin{aligned} Du^n=\frac{u^n-u^{n-1}}{\Delta t}, \qquad n=1,\ldots ,M. \end{aligned}$$

(7)

for which we have the following result.

Theorem 2.3

In the conditions of Theorem 2.1 the following bound holds:

$$\begin{aligned} \biggr (\Delta t\sum _{n=1}^M \bigl \Vert (I-P_X^r)Du^n\bigr \Vert _X^2\biggr )^{\frac{1}{2}}\le 2c_m \biggl ({r_MT}\sum _{k>r} \sigma _k^2\biggr )^{\frac{m-1}{2m}} \bigl \Vert (I-P_X^r)\partial _t u\Vert _{H^{m-1}(0,T,X)}^{\frac{1}{m}}. \end{aligned}$$

Proof

The proof is a direct consequence of estimate (72) in Theorem 4.12 below applied to $f=u-P_X^r u$, the identity (3) and (5). $\square$

Remark 2.4

An important case in practice in that of periodic orbits, since they are key elements in bifurcation diagrams of many dynamical systems associated to PDEs. In this case, the snapshot $u_0$ can be omitted in (2) and (3), and $M+1$ can be replaced by M in previous formulae (see also Sect. 4.1) and, consequently, the ratio $r_M$ in (6) can be replaced by 1. Also, in the estimates in Theorems 2.1 and 2.2 one can replace the constant $c_m$ by 1, which gives much more favourable estimates (see values of constants $c_m$ in Table 7 as well as $\bigl \Vert (I-P_X^r)\partial _t u\bigr \Vert _{H^{m-1}(0,T,X)}$ can be replaced by $\bigl \Vert (I-P_X^r)\partial _t^m u\bigr \Vert _{L^2(0,T,X)}$, that is

$$\begin{aligned}&\max _{0\le n\le M} \bigl \Vert u^n - P_X^r u^n\bigr \Vert _X \le \sqrt{2} c_A\biggl ({T}\sum _{k>r} \sigma _k^2\biggr )^{\frac{1}{2}-\frac{1}{4m}}\bigl \Vert (I-P_X^r)\partial ^m_t u\bigr \Vert _{L^2(0,T,X)}^{\frac{1}{2m}} \nonumber \\&\hspace{8pc} +\biggl (\sum _{k>r} \sigma _k^2\biggr )^{\frac{1}{2}}, \end{aligned}$$

(8)

$$\begin{aligned}&\biggr (\Delta t\sum _{n=1}^M \bigl \Vert (I-P_X^r)Du^n\bigr \Vert _X^2\biggr )^{\frac{1}{2}}\le 2\biggl ({T}\sum _{k>r} \sigma _k^2\biggr )^{\frac{1}{2}-\frac{1}{2m}} \bigl \Vert (I-P_X^r)\partial _t^m u\bigr \Vert _{L^2(0,T,X)}^{\frac{1}{m}}. \end{aligned}$$

(9)

As in Theorem 2.1, the second term on the right-hand side of (8) can be omitted if the snapshots have zero mean. The proof of these estimates follows by applying Theorem 4.11 to $(I-P_X^r) u$.

Some reduction in the size of the constants $c_m$ can be obtained also when computing quasi periodic orbits in an invariant tori if one uses the techniques described in [17] to compute them, since although $u(T)\ne u(0)$, one still has $\left\| u(T)-u(0)\right\| \ll 1$, and one can modify the technique so that this is also the case with first derivatives or higher order ones.

Remark 2.5

In the analysis of POD methods, as it will be the case in next section, one usually has to estimate $(I-P_X^r)$ in a norm $\Vert \cdot \Vert$ other than that of X. If $\left\| \cdot \right\|$ is the norm of a Hilbert space W containing the snapshots $u^0,\ldots , u^M$, then one can use [12, Lemma 2.2] to get

$$\begin{aligned} \frac{1}{M+1} \sum _{n=0}^m \bigl \Vert (I-P_X^r)u^n\bigr \Vert ^2 = \sum _{k>r} \sigma _k^2 \bigl \Vert \varphi ^k\bigr \Vert ^2. \end{aligned}$$

(10)

Applying this estimate instead of the identity (3) in the proofs of Theorems 2.2 and 2.3 one gets the following estimates

$$\begin{aligned}&\max _{0\le n\le M} \bigl \Vert u^n - P_X^r u^n\bigr \Vert \le \sqrt{2} c_Ac_m^{\frac{1}{2}} \biggl ({r_MT}\sum _{k>r} \sigma _k^2 \bigl \Vert \varphi ^k\bigr \Vert ^2\biggr )^{\frac{1}{2}-\frac{1}{4m}}\bigl \Vert (I-P_X^r)\partial _t u\bigr \Vert _{H^{m-1}(0,T,W)}^{\frac{1}{2m}} \nonumber \\&\hspace{7.5pc} +\biggl ({r_M}\sum _{k>r} \sigma _k^2\bigl \Vert \varphi ^k\bigr \Vert ^2\biggr )^{\frac{1}{2}}. \end{aligned}$$

(11)

$$\begin{aligned}&\biggr (\Delta t\sum _{n=1}^M \bigl (I-P_X^r)Du^n\bigr \Vert ^2\biggr )^{\frac{1}{2}}\!\! \nonumber \\&\qquad \le 2c_m \biggl ({r_MT}\sum _{k>r} \sigma _k^2 \bigl \Vert \varphi ^k\bigr \Vert ^2\biggr )^{\frac{m-1}{2m}}\! \bigl \Vert (I-P_X^r)\partial _t u\bigr \Vert _{H^{m-1}(0,T,W)}^{\frac{1}{m}}. \end{aligned}$$

(12)

As in Remark 2.4, when u is periodic in t with period T, then, $c_m$ can be replaced by 1, $\bigl \Vert (I-P_X^r)\partial _t u\bigr \Vert _{H^{m-1}(0,T,W)}$ by $\bigl \Vert (I-P_X^r)\partial _t^m u\Vert _{L^2(0,T,W)}$ and $r_M$ can also be replaced by 1.

2.1 Application to a POD Method

We now apply the previous results to obtain pointwise error bounds for a POD method applied to the heat equation where no DQ were included in the data set to obtain the POD basis $\{\varphi _1,\ldots ,\varphi _J\}$. To discretize the time variable we consider two methods, the implicit Euler method and the second-order backward differentiation formula (BDF2). Analysis similar to part of computations done in the present section has been done before (see e.g., [6, Lemma 3]) but it is carried out here because better error constants are obtained.

Let us assume that u is a semi-discrete FE approximation to the solution of the heat equation with a forcing term f so that $u(t)\in V$ for some FE space V of piecewise polynomials over a triangulation and satisfies

$$\begin{aligned} (\partial _t u,\varphi ) + \nu (\nabla u,\nabla \varphi ) = (f,\varphi ), \quad \forall \varphi \in V, \end{aligned}$$

(13)

where $\nu >0$ is the thermal diffusivity and, in this section, $(\cdot ,\cdot )$ denotes the standard inner product of $L^2(\Omega )$. We consider the POD method

$$\begin{aligned} (Du_r^n,\varphi ) + \nu (\nabla u_r^n,\nabla \varphi ) = (f,\varphi ),\qquad \forall \varphi \in V_r, \qquad n=1,\ldots , M, \end{aligned}$$

(14)

with

$$\begin{aligned} u_r^0=R_ru(\cdot ,0), \end{aligned}$$

(15)

where $R_r$ denotes the Ritz projection,

$$\begin{aligned} (\nabla R_r u,\nabla \varphi ) = (\nabla u,\nabla \varphi ),\qquad \forall \varphi \in V_r. \end{aligned}$$

Instead of using the first-order convergent Euler method considered above we may use the BDF2, with gives the the following method

$$\begin{aligned} (\mathcal{D}u_r^n,\varphi ) + \nu (\nabla u_r^n,\nabla \varphi ) = (f,\varphi ),\qquad \forall \varphi \in V_r, \qquad n=2,\ldots , M, \end{aligned}$$

(16)

where

$$\begin{aligned} \mathcal{D} u_r^n = \frac{3}{2} D u_r^n - \frac{1}{2}Du_r^{n-1}, \qquad n=2,\ldots ,M, \end{aligned}$$

(17)

and, for simplicity,

$$\begin{aligned} u_r^n=P_X^r u^n,\qquad n=0,1. \end{aligned}$$

(18)

We now prove the following result.

Theorem 2.6

Let X be $H^1_0$ and let $p=1$ in the case of method (14–15) and $p=2$ otherwise. Assume that $u\in H^{p+1}(0,T,L^2)\cap H^{m}(0,T,H^1_0)$ for some $m\ge 2$. Then, the following bound holds for $0\le n\le M$:

$$\begin{aligned} \big \Vert u_r^n - u^n\big \Vert&\le 4C_P\sqrt{T}c_m \bigg ({r_MT}\sum _{k>r} \sigma _k^2\bigg )^{\frac{1}{2}- \frac{1}{2m}} \big \Vert (I-P_X^r)\partial _t u\big \Vert _{H^{m-1}(0,T,H^1_0)}^{\frac{1}{m}} \nonumber \\&\quad +\sqrt{2}C_P c_Ac_m^{1/2} \bigg ({r_MT}\sum _{k>r} \sigma _k^2\bigg )^{\frac{1}{2}- \frac{1}{4m}}\big \Vert (I-P_X^r)\partial _t u\big \Vert _{H^{m-1}(0,T,H^1_0)}^{\frac{1}{2m}} \nonumber \\&\quad + \bigg ({r_M}\sum _{k>r} \sigma _k^2\bigg )^{\frac{1}{2}} + \sqrt{p+3}(\Delta t)^p\sqrt{T} \left\| \partial _t^{p+1}u\right\| _{L^2(0,T,L^2)}. \end{aligned}$$

(19)

Proof

Since the POD basis $\{\varphi _1,\ldots ,\varphi _J\}$ has been computed with respect to the inner product in $H^1_0$, we have $P_X^r=R_r$. We first analyze method (14–15). We notice that

$$\begin{aligned} (DP_X^ru^n,\varphi ) + \nu (\nabla P_X^r u^n,\nabla \varphi )=(f,\varphi ) + (\tau ^n,\varphi ), \qquad \forall \varphi \in V_r, \end{aligned}$$

(20)

where

$$\begin{aligned} \tau ^n = DP_X^r u^n - \partial _tu(\cdot ,t_n),\qquad n=1,\ldots ,M. \end{aligned}$$

Subtracting (20) from (14), for the error

$$\begin{aligned} e_r^n=u_r^n - P_X^r u^n,\qquad n=0,\ldots ,M, \end{aligned}$$

we have the following relation,

$$\begin{aligned} (De_r^n,\varphi ) + \nu (\nabla e_r^n,\nabla \varphi ) = (\tau ^n,\varphi ),\qquad \forall \varphi \in V_r, \qquad n=1,\ldots , M. \end{aligned}$$

(21)

Taking $\varphi =\Delta t e_r^n$ and using that $(e_r^n - e_r^{n-1},e_r^n) = (\bigl \Vert e_r^n \bigr \Vert ^2 - \bigl \Vert e_r^{n-1} \bigr \Vert ^2 + \bigl \Vert e_r^n-e_r^{n-1} \bigr \Vert ^2)/2$, one obtains

$$\begin{aligned} \bigl \Vert e_r^n \bigr \Vert ^2 - \bigl \Vert e_r^{n-1} \bigr \Vert ^2 +2\nu {\Delta t}\bigl \Vert \nabla e_r^n\bigr \Vert ^2 \le 2{\Delta t}\bigl \Vert \tau ^n\bigr \Vert \bigl \Vert e_r^n\bigr \Vert , \end{aligned}$$

(22)

If $\bigl \Vert e_r^n\bigr \Vert > \bigl \Vert e_r^{n-1}\bigr \Vert$, then $-1< -\bigl \Vert e_r^{n-1}\bigr \Vert /\bigl \Vert e_r^n\bigr \Vert$. Hence, dividing both sides of (22) by $\bigl \Vert e_r^n\bigr \Vert$ we get

$$\begin{aligned} \bigl \Vert e_r^n \bigr \Vert - \bigl \Vert e_r^{n-1} \bigr \Vert \le 2{\Delta t}\bigl \Vert \tau ^n\bigr \Vert . \end{aligned}$$

(23)

If, on the contrary, $\bigl \Vert e_r^n\bigr \Vert \le \bigl \Vert e_r^{n-1}\bigr \Vert$, for the right-hand side in (22) we write $\bigl \Vert \tau ^n\bigr \Vert \bigl \Vert e_r^n\bigr \Vert \le \bigl \Vert \tau ^n\bigr \Vert ( \bigl \Vert e_r^n\bigr \Vert + \bigl \Vert e_r^{n-1}\bigr \Vert )/2$ so that dividing both sides of (22) by $\bigl \Vert e_r^n\bigr \Vert + \bigl \Vert e_r^{n-1}\bigr \Vert$, we also obtain (23). Summing from $n=1$ to $n=m$ and using (15) we obtain

$$\begin{aligned} \bigl \Vert e_r^m \bigr \Vert \le 2\Delta t\sum _{n=1}^m \bigl \Vert \tau ^n\bigr \Vert \le 2\sqrt{T} \biggl (\Delta t\sum _{n=1}^m \bigl \Vert \tau ^n\bigr \Vert ^2\biggr )^{\frac{1}{2}}, \end{aligned}$$

(24)

where, in the last step we have applied Hölder’s inequality.

With respect to $\tau ^n$, by adding $\pm Du^n$ we have

$$\begin{aligned} \bigl \Vert \tau _n\bigr \Vert \le \bigl \Vert (I-P_X^r) Du^n\bigr \Vert + \big \Vert Du^n- \partial _t u(\cdot ,t_n)\bigr \Vert . \end{aligned}$$

If $u\in H^2(0,T,L^2)$ Taylor expansion with integral remainder allows us to write

$$\begin{aligned} \big \Vert Du^n- \partial _t u(\cdot ,t_n)\bigr \Vert&\le \frac{1}{\Delta t}\biggl \Vert \int _{t_{n-1}}^{t_n} \!\!(t-t_{n-1}) \partial ^2_{t} u(\cdot ,t)\,\textrm{d}t\biggr \Vert \le \sqrt{\Delta t} \bigl \Vert \partial ^2_t u\bigr \Vert _{L^2(t_{n-1},t_n,L^2)}. \end{aligned}$$

Thus, from (24) we get

$$\begin{aligned} \bigl \Vert e_r^m \bigr \Vert \le 2\sqrt{T} \biggl (\Delta t\sum _{n=1}^m\bigl \Vert (I-P_X^r)D u^n\bigr \Vert ^2\biggr )^{\frac{1}{2}} + 2\Delta t\sqrt{T} \bigl \Vert \partial _t^2u\bigr \Vert _{L^2(0,T,L^2)}. \end{aligned}$$

Using Poincaré inequality

$$\begin{aligned} \bigl \Vert v\bigr \Vert \le C_P \bigl \Vert \nabla v\bigr \Vert ,\qquad \forall v\in H^1_0(\Omega ), \end{aligned}$$

(25)

and applying Theorem 2.3 we have

$$\begin{aligned} \max _{0\le n \le M} \bigl \Vert e_r^n\bigr \Vert \le &4c_mC_P\sqrt{T} \biggl ({r_MT}\sum _{k>r} \sigma _k^2\biggr )^{\frac{m-1}{2m}} \bigl \Vert (I-P_X^r)\partial _t u\bigr \Vert _{H^{m-1}(0,T,H^1_0)}^{\frac{1}{m}} \nonumber \\& + 2\Delta t\sqrt{T} \left\| \partial _t^2u\right\| _{L^2(0,T,L^2)}. \end{aligned}$$

Finally, to estimate the errors $u^n-u_r^n$ we write $u_r^n - u^n = e_r^n + P_X^r u^n-u^n$, and apply (25) and Theorem 2.2 to conclude (19).

The analysis of method (16–18) is very similar to that of (14), and we comment on the differences next. As it is well-known (and a simple calculation shows) $(\mathcal{D}e_r^n,e_r^n)=\mathcal{E}_n^2 - \mathcal{E}_{n-1}^2$, where

$$\begin{aligned} \mathcal{E}_n =\frac{1}{2} \left( \bigl \Vert e_r^n\bigr \Vert ^2 + \bigl \Vert 2e_r^n - e_r^{n-1}\bigr \Vert ^2\right) ^{1/2}, \quad n=1,\ldots ,M. \end{aligned}$$

It is easy to check that $\left\| e_r^n \right\| \le \mathcal{E}_n$, so that one can repeat (with obvious changes) the analysis above with the implicit Euler method with $\left\| e_r^n\right\|$ replaced by $\mathcal{E}_n$ to reach

$$\begin{aligned} \bigl \Vert e_r^m \bigr \Vert \le \mathcal{E}_m \le \Delta t\sum _{n=2}^m \bigl \Vert \mathcal{T}^n\bigr \Vert \le \sqrt{T} \biggl (\Delta t\sum _{n=2}^m \bigl \Vert \mathcal{T}^n\bigr \Vert ^2\biggr )^{\frac{1}{2}}, \end{aligned}$$

(26)

instead of (24), where we have used that $\mathcal{E}_1=0$ due to (18), and where

$$\begin{aligned} \mathcal{T}^n = P_X^r \mathcal{D} u^n - \partial _t u(\cdot ,t_n) = (P_X^r-I) \mathcal{D} u^n + \mathcal{D} u^n - \partial _t u(\cdot , t_n). \end{aligned}$$

For the last term above we have (see e.g., [6, Lemma 4])

$$\begin{aligned} \bigl \Vert \mathcal{D} u^n - \partial _t u(\cdot , t_n)\bigr \Vert \le \sqrt{5}(\Delta t)^{3/2} \biggl (\int _{t_{n-2}}^{t_n} \bigl \Vert \partial _{t}^3 u(\cdot ,t)\bigr \Vert ^2\,\textrm{d}t\biggr )^{\frac{1}{2}}. \end{aligned}$$

Consequently, from (26) and noticing that $\bigl \Vert \mathcal{D}e_r^n\bigr \Vert \le (3/2)\bigl \Vert De_r^n\bigr \Vert + (1/2)\bigl \Vert De_r^{n-1}\bigr \Vert$, we have

$$\begin{aligned} \bigl \Vert e_r^m\bigr \Vert \le 2\sqrt{T} \biggl (\Delta t\sum _{n=1}^m \bigl \Vert (I-P_X^r) Du^n\bigr \Vert ^2\biggr )^{1/2} + \sqrt{5T} (\Delta t)^2 \bigl \Vert \partial _t^3 u\bigr \Vert _{L^2(0,T,L^2)}, \end{aligned}$$

(27)

so that applying (25) and Theorem 2.3 it follows that

$$\begin{aligned} \max _{0\le n \le M} \bigl \Vert e_r^n\bigr \Vert \le&4c_mC_P\sqrt{T} \biggl ({r_MT}\sum _{k>r} \sigma _k^2\biggr )^{\frac{m-1}{2m}} \bigl \Vert (I-P_X^r)\partial _t u\bigr \Vert _{H^{m-1}(0,T,H^1_0)}^{\frac{1}{m}} \nonumber \\& + (\Delta t)^2\sqrt{5T} \left\| \partial _t^3u\right\| _{L^2(0,T,L^2)}, \end{aligned}$$

and, for the error $u_r^n - u = e_r^n + (I-P_X^r) u_n$, applying Theorem 2.2 we get (19). $\square$

Remark 2.7

In view of Remark 2.5, in the above estimates we may replace the Poincaré constant $C_P$ by 1, $\sigma _k^2$ by $\sigma _k^2\bigl \Vert \varphi _k\bigr \Vert ^2$ and the norm $\left\| \cdot \right\| _{H^{m-1}(0,T,H^1_0)}$ by $\left\| \cdot \right\| _{H^{m-1}(0,T,L^2)}$. Also in view of Remark 2.4, when u is periodic in t with period T, the constant $c_m$ can be replaced by 1 and $\bigl \Vert (I-P_X^r)\partial _t u\bigr \Vert _{H^{m-1}(0,T,H^1_0)}$ by $\bigl \Vert (I-P_X^r)\partial _t^m u\bigr \Vert _{L^2(0,T,H^1_0)}$ (or by $\bigl \Vert (I-P_X^r)\partial _t^m u\bigr \Vert _{L^2(0,T,L^2)}$ if we use the estimates in Remark 2.5).

Remark 2.8

If, for the method (16), $u_r^1$ is computed from $u_r^0$ with one step of the implicit Euler method, instead of setting $u_r^1=P_X^r u^1$, then one can use a general stability result for the BDF2 like [6, Lemma 3] and then, use standard estimates to express the term $Du^1 - \partial _t u(\cdot , t_1)$ in $\tau ^1$ as $\big \Vert Du^1- \partial _t u(\cdot ,t_1)\bigr \Vert \le {\Delta t} \bigl \Vert \partial ^2_t u\bigr \Vert _{L^\infty (0,t_1,L^2)}.$ Thus, one gets estimates similar to (19) but with different constants multiplying the different terms and $\bigl \Vert \partial _t^3u\bigr \Vert _{L^2(0,T,L^2)}$ replaced by $\bigl \Vert \partial _t^3u\bigr \Vert _{L^2(0,T,L^2)} + \bigl \Vert \partial ^2_t u\bigr \Vert _{L^\infty (0,t_1,L^2)}$.

Remark 2.9

If $X=L^2$, that is, if the POD basis is computed with respecto to the $L^2$ inner product then, instead of $(\tau ^n,\varphi )$ in (20), one has $(\tau ^n,\varphi ) + \nu (\nabla (P_X^r -I)u^n,\nabla \varphi )$ and, thus, arguing as above, one has to estimate

$$\begin{aligned} \nu \Delta t\sum _{n=1}^m \left\| \nabla (P_X^r -I)u^n\right\| _0^2 \end{aligned}$$

which can be bounded in terms of the stiffness matrix of the POD basis or, according to [12, Lemma 2.2] can be bounded in terms of

$$\begin{aligned} \Delta t\sum _{k>r} \sigma _k^2\left\| \nabla \varphi _k\right\| _0^2. \end{aligned}$$

Although in many practical problems one can check that the sum above is only a moderate factor larger than $\sum _{r>k} \sigma _k^2$, at present, the only rigorous bound available is proportional to $C_Ph^{-2}\sum _{r>k} \sigma _k^2$, where h is the mesh diameter of the FE mesh. The same can be said of the stiffness matrix of the POD basis. Consequently, at present, it is not possible to prove optimal bounds if the POD basis is computed with respect to the $L^2$ inner product.

3 Numerical Experiments

3.1 Test 1: The Brusselator with Diffusion

We now check some of the estimates of previous sections. For the snapshots, we consider the semi-discrete piecewise quadratic FE approximation over a uniform $80\times 80$ triangulation (with diagonals running southwest-northeast) of the unit square of the stable periodic orbit of the following system, which, in the abssence of diffusion, is known as the Brusselator (see e.g., [14, p. 115]):

$$\begin{aligned} \begin{array}{rclcl} u_t& =& \nu \Delta u +1 +u^2v - 4 u,& \qquad & (t,x)\in \Omega \times (0,T],\\ v_t & =& \nu \Delta v+3 u -u^2v,& \qquad & (t,x)\in \Omega \times (0,T],\\ & & u(x,t)=1, \quad v(x,t) =3,& & (t,x)\in \Gamma _1\times (0,T],\\ & & \partial _n u(x,t)=\partial _n v(t,x) =0,& & (x,t)\in \Gamma _2\times (0,T],\\ \end{array} \end{aligned}$$

(28)

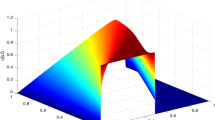
where $\nu =0.002$, $\Omega =[0,1]\times [0,1]$, $\Gamma _1\subset \partial \Omega$ is the union of sides $\{x=1\}\bigcup \{ y=1\}$, and $\Gamma _2$ is the rest of $\partial \Omega$ (see [7] for details). This system was chosen for numerical test in [7] because it has a stable limit cycle, and, hence, nontrivial asymptotic dynamics, as opposed to many reaction-diffusion systems where solutions tend to a steady state as time tends to infinity. The period of this limit cycle is $T=7.090636$ (up to 7 significant digits). This system is particularly challenging for the size of its time derivatives, which, as it can be seen in Fig. 1, they vary considerably over one period.

Fig. 1

$L^2$ norms of the time derivatives of the finite element approximation ${\varvec{u}}_h$ to the periodic orbit solution of (28)

In what follows, $M=256$. We took values ${\varvec{u}}(\cdot , t_n)=[u(\cdot ,t_n),v(\cdot , t_n)]^T$, $n=0,\ldots ,M$, and, in order to have snapshots taking value zero on $\Gamma _1$ we subtracted their mean so that ${\varvec{u}}^n = {\varvec{u}}(\cdot ,t_n) - m_0$, where $m_0=({\varvec{u}}(\cdot ,t_1)+\cdots +{\varvec{u}}(\cdot ,t_M))/M$ (notice that being ${\varvec{u}}$ periodic with period T, there is no need to include ${\varvec{u}}(\cdot ,0)$ in the data set to obtain the POD basis, since ${\varvec{u}}(\cdot ,0)={\varvec{u}}(\cdot ,T)$).

We first check estimate (8) for $X=L^2$ and two values of r, $r=24$ and $r=31$. The value of $r=24$ was chosen because it was the first value of r for which $\gamma _r$ in (30) was below $5.35\times 10^{-5}$, which, as explained in [7], is the maximum error of the snapshots with respect the true solution of (28) (recall that the snapshots are FE approximations, not the true solution). The value $r=31$ was chosen for comparison. We have the following values for the left-hand side and tail of the singular values

$$\begin{aligned} \max _{1\le n\le M} \bigl \Vert (I-P_X^r){\varvec{u}}^n\bigr \Vert _X ={\left\{ \begin{array}{rcr} 1.63\times 10^{-4},& \ & r=24,\\ 1.47\times 10^{-5},& & r=31,\end{array}\right. } \end{aligned}$$

(29)

$$\begin{aligned} \gamma _r\equiv \biggl (\sum _{k>r} \sigma _k^2\biggr )^{1/2} = {\left\{ \begin{array}{rcr} 4.61\times 10^{-5},& \ & r=24,\\ 4.56\times 10^{-6},& & r=31,\end{array}\right. } \end{aligned}$$

(30)

and Table 2 shows the right-hand side of (8). We notice that there is an overestimation by a factor of 20.

Table 2 Test 1. Right-hand side of (8) for $X=L^2$ and different values of m

We now check estimates (9) and (12) when $W=L^2(\Omega )$ and $\left\| \cdot \right\|$ its norm, which have been used in (27) in the previous section to obtain estimate (19) and in Remark. 2.7. We have the following values

$$\begin{aligned} \biggr (\Delta t\sum _{n=1}^M \bigl \Vert (I-P_X^r)D{\varvec{u}}^n\bigr \Vert ^2\biggr )^{\frac{1}{2}} ={\left\{ \begin{array}{lcl} 9.41\times 10^{-3},& \ & r=24,\\ 8.60\times 10^{-4},& & r=31.\end{array}\right. } \end{aligned}$$

(31)

Notice that $X=H^1_0$ but we are measuring $(I-P_X^r)D{\varvec{u}}^n$ in the $L^2$ norm. Applying Poincaré inequality (25) and (9) the quantity above can be estimated by

$$\begin{aligned} \rho _m \equiv 2C_P\biggl (\sum _{k>r} \sigma _k^2\biggr )^{\frac{1}{2}-\frac{1}{2m}} \bigl \Vert \nabla (I-P_X^r)\partial _t^m {\varvec{u}}\bigr \Vert _{L^2(0,T,L^2)}^{\frac{1}{m}}. \end{aligned}$$

(32)

On the other hand according to Remark 2.7, and taking into account that we are in the periodic case, it can also be estimated by

$$\begin{aligned} \mu _m \equiv 2\biggl (\sum _{k>r} \sigma _k^2\bigl \Vert \varphi _k\bigr \Vert ^2\biggr )^{\frac{1}{2}-\frac{1}{2m}} \bigl \Vert (I-P_X^r)\partial _t^m {\varvec{u}}\bigr \Vert _{L^2(0,T,L^2)}^{\frac{1}{m}}. \end{aligned}$$

(33)

Table 3 shows the corresponding values. Notice that $C_P=\lambda ^{-1/2}$, where $\lambda$ is the smallest eigenvalue of the $-\Delta$ operator subject to homogeneous Dirichlet boundary condition on $\Gamma _1$ and homogeneous Neumann boundary condition on $\Gamma _2$, and, thus, $C_P=\sqrt{2}/\pi$. By comparing the values in Table 3 with those in (31), we can see that while $\rho _m$ is not a good estimate, $\mu _m$ slightly overestimates the quantities in (31) by a factor that does not reach 3.1.

Table 3 Test 1. Estimates (32) and (33) for (31)

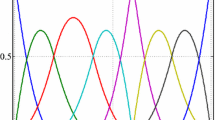
The fact that $\mu _m$ is a much better estimate than $\rho _m$ is explained in part by the size of the values $\bigl \Vert \varphi _k\bigr \Vert$ which, as shown in Fig. 2, they are small and well below the constant $C_P$ (marked with a red dotted line in the plot).

Fig. 2

$L^2$ norms of the elements $\varphi ^1,\ldots ,\varphi ^J$ of the POD basis for $X=H^1_0$ and constant $C_P$ in (25)

3.2 Test 2: Flow Around a Cylinder

We now consider the well-known benchmark problem defined in [18] associated to the Navier–Stokes equations,

$$\begin{aligned} \begin{array}{rcll} {\varvec{u}}_t -\nu \Delta {\varvec{u}}+ ({\varvec{u}}\cdot \nabla ){\varvec{u}}+ \nabla p & =& {\varvec{f}}& \text {in }\ \Omega \times (0,T], \\ \nabla \cdot {\varvec{u}}& =& 0& \text {in }\ \Omega \times (0,T], \end{array} \end{aligned}$$

(34)

where, as it is well-known, ${\varvec{u}}$ is the velocity field of a fluid moving in the domain $\Omega$, p the kinematic pressure, $\nu >0$ the kinematic viscosity coefficient, and ${\varvec{f}}$ represents the accelerations due to external body forces acting on the fluid. The domain is given by

$$\begin{aligned} \Omega =(0,2.2)\times (0,0.41)/\left\{ (x,y) \mid (x-0.2)^2 + (y-0.2)^2 \le 0.0025\right\} . \end{aligned}$$

On the inflow boundary, $x=0$, the velocity is prescribed by

$$\begin{aligned} {\varvec{u}}(0,y,t)=\frac{6}{0.41^2}\left( \begin{array}{c} y(0.41-y)\\ 0\end{array}\right) , \qquad t\ge 0, \end{aligned}$$

and on the outflow boundary $x=2.2$ we set the so-called “do nothing" boundary condition. On the rest of the boundary the velocity is set ${\varvec{u}}=\textbf{0}$. It is well known that for ${\varvec{f}}=\textbf{0}$ and $\nu =0.001$ there is a stable periodic orbit.

We take the snapshots from the FE approximation to the velocity field ${\varvec{u}}$ computed in [5], which uses 27168 degrees of freedom for the velocity and 3480 for the pressure. It was checked in [5] that the relative errors in the velocity of this approximation are below 0.003 and 0.03 in the the $L^2$ and $H^1$ norms repectively, and the period of the periodic orbit of this approximation is $T=0.331761$. As in the previous section we set $M=256$, and the mean was subtracted to the function values ${\varvec{u}}(\cdot , t_n)$ in order to have snapshots with zero value on the inflow boundary.

This is also a challenging problem because of the size of the derivatives, which are shown in Table 4.

Table 4 Maximum of the $L^2$ norm of the time derivatives of the velocity ${\varvec{u}}$

As in the previous section, we first check estimate (8) for $X=L^2$ and the values of r given by $r=12$ and $r=20$, which were chosen with the same criteria as in Sect. 3.1. The following values for the left-hand of side of (8) and the tail of the singular values are

$$\begin{aligned} \max _{1\le n\le M} \bigl \Vert (I-P_X^r){\varvec{u}}^n\bigr \Vert _X =\left\{ \begin{array}{rcr} 1.86\times 10^{-3},& \ & r=12,\\ 9.62\times 10^{-5},& & r=20,\end{array}\right. \end{aligned}$$

(35)

$$\begin{aligned} \gamma _r\equiv \biggl (\sum _{k>r} \sigma _k^2\biggr )^{1/2} = \left\{ \begin{array}{rcr} 1.76\times 10^{-3},& \ & r=12,\\ 8.95\times 10^{-5},& & r=20,\end{array}\right. \end{aligned}$$

(36)

whereas those of the right-hand side of (8) are given in Table 5, where we appreciate an overestimation by a factor that does not reach the value of 20. We also checked all values of r between $r=11$ and $r=70$, and found that the factor of the overestimation was between 5.6 and 27.4, and the average value was 16.33.

Table 5 Test 2. Right-hand side of (8) for $X=L^2$ and different values of m

In view of the large overestimation of (9) in Sect. 3.1, we only check estimate (12) in the present section. For the left-hand side, we have the following values

$$\begin{aligned} \biggr (\Delta t\sum _{n=1}^M \bigl \Vert (I-P_X^r)D{\varvec{u}}^n\bigr \Vert ^2\biggr )^{\frac{1}{2}} =\left\{ \begin{array}{lcl} 1.56\times 10^{-2},& \ & r=12,\\ 9.65\times 10^{-5},& & r=20,\end{array}\right. \end{aligned}$$

(37)

and in Table 6 we have those of the right-hand side. We see that the values of $\mu _m$ overestimate (37) by a factor that does not reach 23. Indeed, repeating these computations for r ranging from $r=11$ to $r=80$, we found that the values of $\mu _m$ for $m=2,3,4,5$ were at least three times larger than those of the left-hand side of (12), but the overestimation was always by a factor below 26, the average factor being 10.3.

Table 6 Test 2. Estimate (33) for (37)

We now test the non periodic case. For this, we consider equally spaced snapshots over half a period and take $M=128$. We first check that we are in the general case by computing the value $\Vert {\varvec{u}}^M - {\varvec{u}}^0\Vert /\max ( \Vert {\varvec{u}}^0\Vert ,\Vert {\varvec{u}}^M\Vert )$, which turned out to be 1.66. With respect to estimates (11) and (12) we check if the values of the constants $c_m$ in Table 7 are sharp or if they are a consequence of the techniques used in the proofs. We can see this by checking if the more benign estimates of the periodic case (where $c_m=1$) also hold for non periodic functions. This seems to be the case as it can be seen in Fig. 3, where, for both plots, the blue lines which correspond to the left-hand sides of estimates (11) and (12) are below the rest of the values, which correspond to the right-hand sides of the estimates (8) and (9) of the periodic case. We checked that the ratio of $\max \Vert (I-P_X) u_n\Vert$ over the right-hand side of (8) in the left plot never exceded 18, and that of the left-hand side of (12) over $\mu _m$, $m=2,3,4,5$ in the right-plot never exceded 22. These suggests that, perhaps with different techniques for the proofs, the estimates for the general case may be improved. However, this will be subject of future work.

Table 7 The first five values of coefficient $c_m$ in (62)

Fig. 3

Left: left-hand side of (11) and right-hand side of (8). Right: left-hand side of (12) and values of $\mu _m$ in (33) for $m=2,3,4,5$

4 Abstract Results

In this section we state and prove a series of results which are needed to prove those in Sect. 2. We do this in a more general setting.

Let X be a Hilbert space with inner product $(\cdot ,\cdot )$ and associated norm $\bigl \Vert \cdot \bigr \Vert$. In order to have shorter subindices in this section for $T>0$ and positive integer M we denote

$$\begin{aligned} \tau =T/M, \end{aligned}$$

instead of $\Delta t$ as in previous sections. Thus, we write, $t_n=n\tau$, $n=0,\ldots ,M$. For a sequence $f_\tau =(f_n)_{n=0}^M$ in X we denote

$$\begin{aligned} Df_n=D^1 f_n = \frac{f_n-f_{n-1}}{\tau },\qquad n=1,\ldots ,M, \end{aligned}$$

and, for $k=2,\ldots \,J$,

$$\begin{aligned} D^k f_n= \frac{D^{k-1} f_n - D^{k-1} f_{n-1}}{\tau },\qquad n=k,\ldots ,J. \end{aligned}$$

(Notice the backward notation). Also, for simplicity we will use

$$\begin{aligned} D^0 f_n=f_n,\qquad n=0,\ldots ,M. \end{aligned}$$

We define

$$\begin{aligned} \bigl \Vert f_\tau \bigr \Vert _{0}&=\biggl ( \tau \sum _{n=0}^{M}\bigl \Vert f_n\bigr \Vert ^2 \biggr )^{1/2}, \end{aligned}$$

(38)

$$\begin{aligned} \bigl \Vert Df_\tau \bigr \Vert _{0}&=\biggl ( \tau \sum _{n=1}^{M}\bigl \Vert Df_n\bigr \Vert ^2 \biggr )^{1/2}, \end{aligned}$$

(39)

The proof of the following lemma is the discrete counterpart of the following identity and estimate

$$\begin{aligned} \left\| f(t_n)\right\| ^2&=\left\| f(t_m)\right\| ^2 +2 \int _{t_m}^{t_n} (f(s),f'(s))\, \textrm{d}s \\& \le \left\| f(t_m)\right\| ^2 +2{ \left\| f\right\| _{L^2(0,T,X)} \bigl \Vert f'\bigr \Vert _{L^2(0,T,X)}}. \end{aligned}$$

Lemma 4.1

Let $f_\tau =(f_n)_{n=0}^M$ a sequence in X satisfying that $f_0+\cdots +f_M=0$. Then

$$\begin{aligned} \bigl \Vert f_n\bigr \Vert \le c_A\bigl \Vert f_\tau \bigr \Vert _0^{1/2} \bigl \Vert Df_\tau \bigr \Vert _0^{1/2},\qquad n=0,\ldots ,M, \end{aligned}$$

where

$$\begin{aligned} c_A = \sqrt{2 + 2/3}. \end{aligned}$$

(40)

Proof

For $0\le m<n$, we write

$$\begin{aligned} \bigl \Vert f_n\bigr \Vert ^2 - \bigl \Vert f_m\bigr \Vert ^2&= \bigl \Vert f_n\bigr \Vert ^2 - \bigl \Vert f_{n-1}\bigr \Vert ^2 +\cdots + \bigl \Vert f_{m+1}\bigr \Vert ^2 - \bigl \Vert f_m\bigr \Vert ^2 \nonumber \\ &= \sum _{j=m+1}^n \textrm{Re}((f_j+f_{j-1}, f_j-f_{j-1})) \nonumber \\ &\le \tau \sum _{j=m+1}^n \bigl \Vert f_j+f_{j-1}\bigr \Vert \bigl \Vert Df_j\bigr \Vert . \end{aligned}$$

Now applying Hölder’s inequality and noticing that $\bigl \Vert a+b\bigr \Vert ^2 \le 2\bigl \Vert a\bigr \Vert ^2 + 2\bigl \Vert b\bigr \Vert ^2$, we have

$$\begin{aligned} \bigl \Vert f_n\bigr \Vert ^2- \bigl \Vert f_m\bigr \Vert ^2 \le \biggl (2\tau \bigl \Vert f_n\bigr \Vert ^2 + 4\tau \sum _{j=m+1}^{n-1} \bigl \Vert f_j\bigr \Vert ^2+2\tau \bigl \Vert f_m\bigr \Vert ^2 \biggr )^{1/2} \bigl \Vert D f_\tau \bigr \Vert _0, \end{aligned}$$

(41)

and, hence,

$$\begin{aligned} \bigl \Vert f_n\bigr \Vert ^2- \bigl \Vert f_m\bigr \Vert ^2&\le 2\bigl \Vert f_\tau \bigr \Vert _0 \bigl \Vert Df_\tau \bigr \Vert _0. \end{aligned}$$

(42)

A similar argument also shows (42) for $n<m\le M$.

Also, for $0\le l\le m$, we have $f_m =f_l + \tau (Df_{l+1} + \cdots + Df_m)$, so that applying Hölder’s inequality it follows that

$$\begin{aligned} \bigl \Vert f_m - f_l \bigr \Vert \le \sqrt{\left| m-l\right| \tau } \bigl \Vert D f_\tau \bigr \Vert _0. \end{aligned}$$

(43)

A similar argument shows that (43) also holds for $m<l \le M$. Now, since we are assuming that $f_\tau$ is of zero mean, we can write

$$\begin{aligned} f_m =f_m -\frac{1}{M+1}\sum _{l=0}^M f_l= \frac{1}{M+1}\sum _{l\ne m} (f_m -f_l), \end{aligned}$$

and, thus, taking norms, applying (43)

$$\begin{aligned} \bigl \Vert f_m\bigr \Vert \le \frac{\sqrt{\tau }}{M+1} \biggl ( \sum _{l\ne m} \left| m-l\right| ^{1/2}\biggr )\bigl \Vert Df_\tau \bigr \Vert _0. \end{aligned}$$

Now, a simple calculation shows that

$$\begin{aligned} \frac{1}{M+1} \sum _{l\ne m} \left| m-l\right| ^{1/2}\le \frac{1}{M+1} \sum _{l=1}^M l^{1/2} \end{aligned}$$

and it is not difficult to prove that the last expresion does not exceed $(2/3)\sqrt{M}$. Thus, it follows that

$$\begin{aligned} \bigl \Vert f_m\bigr \Vert \le \frac{2}{3}\sqrt{T} \bigl \Vert D f_\tau \bigr \Vert _0. \end{aligned}$$

(44)

We now take m such that

$$\begin{aligned} \bigl \Vert f_m\bigr \Vert = \min _{0\le l\le M} \bigl \Vert f_l\bigr \Vert . \end{aligned}$$

(45)

We have that

$$\begin{aligned} \bigl \Vert f_m\bigr \Vert = \frac{\sqrt{T}}{\sqrt{T}}\bigl \Vert f_m\bigr \Vert = \frac{1}{\sqrt{T}} \left( \tau M\bigl \Vert f_m\bigr \Vert ^2\right) ^{1/2} \le \frac{1}{\sqrt{T}} \bigl \Vert f_\tau \bigr \Vert _0. \end{aligned}$$

(46)

From this inequality and (44) it follows that for $f_m$ satisfying (45) we have

$$\begin{aligned} \bigl \Vert f_m\bigr \Vert ^2 \le {\frac{2}{3}} \bigl \Vert f_\tau \bigr \Vert _0\bigl \Vert Df_\tau \bigr \Vert _0. \end{aligned}$$

This, together with (42) finishes the proof. $\square$

Remark 4.2

Notice that (41) implies (42) also in the case where $\left\| f_\tau \right\|$ is defined as

$$\begin{aligned} \bigl \Vert f_\tau \bigr \Vert _{0}=\biggl (\frac{\tau }{2}\bigl \Vert f_0\bigr \Vert ^2+ \tau \sum _{n=1}^{M-1}\bigl \Vert f_n\bigr \Vert ^2+ \frac{\tau }{2}\bigl \Vert f_M\bigr \Vert ^2 \biggr )^{1/2}, \end{aligned}$$

(47)

and that (46) also holds in this case. Thus, Lemma 4.1 is valid if $\left\| f_\tau \right\|$ is defined as in (47).

Remark 4.3

If the Hilbert space X is either ${\mathbb {R}^d}$ for some $d\ge 0$, or $L^2(\Omega )$, for some $\Omega \subset {\mathbb {R}}^d$ or (a subespace of) the Sobolev space $H^s(\Omega )$ for some integer $s>0$, then the constant $c_A$ in (40) can be set to

$$\begin{aligned} c_A=\sqrt{2}. \end{aligned}$$

(48)

We now show that this is the case for $X=L^2(\Omega )$ since the argument is easily adapted to the other cases. We first notice that since the sequence $f_\tau$ has zero mean, then, for every $x\in ~\Omega$ (except maybe in a set of zero measure) not all values $(f_n(x))_{n=0}^M$ can have the same sign. Consequently, for every $x\in \Omega$ there is an integer $m_x\in [1,M]$ and a value $\lambda _x\in [0,1]$ for which $0=(1-\lambda _x) f_{m_x}(x) +\lambda _x f_{m_x-1}(x) =0$. We notice then that

$$\begin{aligned} f_{m_x}^2(x)= & f_{m_x}(x) f_{m_x}(x) =f_{m_x}(x)(f_{m_x}(x) -((1-\lambda _x) f_{m_x}(x) +\lambda _x f_{m_x-1}(x) )\\= & f_{m_x}(x) \lambda _x(f_{m_x}(x) -f_{m_x-1}(x) ). \end{aligned}$$

Thus, for $x\in \Omega$ such that $m_x \le n$, arguing as in the proof of Lemma 4.1 we may write

$$\begin{aligned} f_n^2(x)&= f_{m_x}^2(x) + \tau \sum _{j=m_x+1}^n \textrm{Re}\left( (f_j(x)+f_{j-1}(x))Df_j(x)\right) \nonumber \\& \le \tau \lambda _x\left| f_{m_x}(x)\right| \left| Df_{m_x}(x)\right| + \tau \sum _{j=m_x+1}^n \left| f_j(x)+f_{j-1}(x)\right| \left| Df_j(x)\right| . \end{aligned}$$

This argument is easily adapted to the case where $m_x>n$. Observe that the last inequality implies

$$\begin{aligned} f_n^2(x) \le \tau \sum _{j=1}^M \left( \left| f_j(x)\right| +\left| f_{j-1}(x)\right| \right) \left| Df_j(x)\right| , \end{aligned}$$

and a similar argument shows that this inequality to be valid also when $m_x>n$. Thus, integrating in $\Omega$ it easily follows that $\left\| f_n\right\| ^2 \le 2\left\| f_\tau \right\| _0 \left\| D f_\tau \right\| _0$.

We now treat first the periodic case, since it is less technical than the general one and the main ideas can be presented more easily.

4.1 The Periodic Case

In this subsection we assume that $f_M=f_0$ and we extend periodically the sequence $f_\tau$, that is $f_{m} = f_{M+m}$ for $m=\pm 1,\pm 2,\ldots \,$. Also, we will consider $\left\| f_\tau \right\| _0$ as defined in (47). We define $\bigl \Vert D^{k} f_\tau \bigr \Vert _{0}$ as

$$\begin{aligned} \bigl \Vert D^kf_\tau \bigr \Vert _{0} =\biggl (\tau \sum _{n=1}^M \bigl \Vert D^k f_n\bigr \Vert ^2\biggr )^{1/2},\quad k=2,\ldots ,M. \end{aligned}$$

(49)

Notice that for $k=1$ the expression above coincides with $\left\| D f_\tau \right\|$ defined in (39). Also, since $f_0=f_M$, the expression in (49) for $k=0$ coincides with the alternative definition of $\left\| f_\tau \right\|$ given in (47), for which, as observed in Remark 4.2 Lemma 4.1 is also valid.

The proof of the following lemma is the discrete counterpart of integration by parts in a periodic function

$$\begin{aligned} \bigl \Vert f'\bigr \Vert ^2 = \int _0^T (f'(t),f'(t))\,\textrm{d}t = -\int _0^T (f(t),f''(t))\,\textrm{d}t \le {\left\| f\right\| _{L^2(0,T,X)} \bigl \Vert f''\bigr \Vert _{L^2(0,T,X)}.} \end{aligned}$$

Lemma 4.4

Let $f_\tau =(f_n)_{n\in {\mathbb {Z}}}$ be a periodic sequence in X with period M. Then, for $k=2,\ldots ,M-1$,

$$\begin{aligned} \bigl \Vert D^kf_\tau \bigr \Vert _0 \le \bigl \Vert D^{k-1} f_\tau \bigr \Vert _0^{1/2} \bigl \Vert D^{k+1} f_\tau \bigr \Vert _0^{1/2} \end{aligned}$$

Proof

Since $\tau \bigl \Vert D^k f_n\bigr \Vert ^2=\tau (D^k f_n, D^k f_n)= (D^k f_n,D^{k-1} f_n - D^{k-1} f_{n-1})$, we have

$$\begin{aligned} \bigl \Vert D^kf_\tau \bigr \Vert _0^2&= \sum _{n=1}^M (D^k f_n, D^{k-1} f_n - D^{k-1} f_{n-1}) \nonumber \\& = (D^kf_M ,D^{k-1}f_M) - (D^kf_1,D^{k-1} f_{0}) - \sum _{n=1}^{M-1} (D^k f_{n+1} - D^kf_n, D^{k-1}f_n). \end{aligned}$$

Now we notice that for the second term on the right-hand side above we have $(D^kf_1,D^{k-1} f_{0})=(D^kf_{M+1},D^{k-1} f_{M})$, and thus

$$\begin{aligned} \bigl \Vert D^kf_\tau \bigr \Vert ^2 = - \sum _{n=1}^{M} (D^k f_{n+1} - D^kf_n, D^{k-1}f_n) =-\tau \sum _{n=1}^{M} (D^{k+1} f_{n+1}, D^{k-1}f_n) \end{aligned}$$

and the proof is finished by applying Hölder’s inequality. $\square$

The proof of the following reuslt follows the ideas in the proof of [1, Lemma 4.12] adapted to the discrete case.

Lemma 4.5

Let $f_\tau =(f_n)_{n\in {\mathbb {Z}}}$ a periodic sequence in X with period M. Then, for $m=2,\ldots ,M$,

$$\begin{aligned} \bigl \Vert D^1 f_\tau \bigr \Vert _0 \le \bigl \Vert f_\tau \bigr \Vert _0^{\frac{m-1}{m}} \bigl \Vert D^mf_\tau \bigr \Vert _0^{\frac{1}{m}}. \end{aligned}$$

(50)

Proof

We will prove below that (50) will be a consequence of the following inequality

$$\begin{aligned} \bigl \Vert D^{k} f_\tau \bigr \Vert _0 \le \bigl \Vert f_\tau \bigr \Vert _0^{\frac{1}{k+1}} \bigl \Vert D^{k+1}f_\tau \bigr \Vert _0^{\frac{k}{k+1}}, \qquad k=1,\ldots ,M-1, \end{aligned}$$

(51)

which we will now proof by induction. Notice that (51) holds for $k=1$ as a direct application of Lemma 4.4. Now assume that (51) holds for $k=1,\ldots ,m-1$, and let us check that it also holds for $k=m$. Applying Lemma 4.4 we have

$$\begin{aligned} \bigl \Vert D^{m} f_\tau \bigr \Vert _0 \le \bigl \Vert D^{m-1} f_\tau \bigr \Vert _0^{1/2} \bigl \Vert D^{m+1}f_\tau \bigr \Vert _0^{1/2}. \end{aligned}$$

Applying the induction hypothesis we have

$$\begin{aligned} \bigl \Vert D^{m} f_\tau \bigr \Vert _0 \le \bigl \Vert f_\tau \bigr \Vert _0^{\frac{1}{2m}}\bigl \Vert D^{m} f_\tau \bigr \Vert _0^{\frac{m-1}{2m}} \bigl \Vert D^{m+1}f_\tau \bigr \Vert _0^{1/2}, \end{aligned}$$

so that dividing by $\bigl \Vert D^{m} f_\tau \bigr \Vert _0^{\frac{m-1}{2m}}$ we obtain

$$\begin{aligned} \bigl \Vert D^{m} f_\tau \bigr \Vert _0^{\frac{m+1}{2m}} \le \bigl \Vert f_\tau \bigr \Vert _0^{\frac{1}{2m}} \bigl \Vert D^{m+1}f_\tau \bigr \Vert _0^{1/2}, \end{aligned}$$

from where (51) follows.

Now, to proof (50), we start with the case $m=2$, which holds as a direct application of Lemma 4.4 for $k=1$. Then we apply (51) repeatedly to the factor with the highest-order difference, that is

$$\begin{aligned} \bigl \Vert D^1 f_\tau \bigr \Vert _0\le & \bigl \Vert f\bigr \Vert ^{\frac{1}{2}} \bigl \Vert D^2f_\tau \bigr \Vert _0^{\frac{1}{2}} \le \bigl \Vert f\bigr \Vert ^{\frac{1}{2}+\frac{1}{6}} \bigl \Vert D^3f_\tau \bigr \Vert _0^{\frac{1}{3}} \le \bigl \Vert f\bigr \Vert ^{\frac{1}{2}+\frac{1}{6} + \frac{1}{12}} \bigl \Vert D^4f_\tau \bigr \Vert _0^{\frac{1}{4}} \\\le & \ldots \le \bigl \Vert f\bigr \Vert ^{\frac{1}{2}+\frac{1}{6} +\cdots \frac{1}{m(m-1)}} \bigl \Vert D^mf_\tau \bigr \Vert _0^{\frac{1}{m}}, \end{aligned}$$

and the proof is finished by noticing that

$$\begin{aligned} \frac{1}{2}+\frac{1}{6} +\cdots \frac{1}{m(m-1)}&= \frac{1}{2} + \left( \frac{1}{2} - \frac{1}{3} \right) + \left( \frac{1}{3} - \frac{1}{4} \right) +\cdots + \left( \frac{1}{m-1} - \frac{1}{m} \right) \nonumber \\ &\le 1 - \frac{1}{m} = \frac{m-1}{m}. \end{aligned}$$

$\square$

From Lemmas 4.1 and 4.5 the following result follows.

Lemma 4.6

Let $f_\tau =(f_n)_{n\in {\mathbb {Z}}}$ a periodic sequence in X with period M and zero mean. Then, for $k=1,\ldots ,M$, the following estimate holds:

$$\begin{aligned} \bigl \Vert f_n\bigr \Vert \le c_A\bigl \Vert f_\tau \bigr \Vert _0^{1-\frac{1}{2m}} \bigl \Vert D^mf_\tau \bigr \Vert _0^{\frac{1}{2m}}, \end{aligned}$$

(52)

where $c_A$ is the constant in (40).

4.2 The General Case

In this section, and unless stated otherwise, $f_\tau =(f_n)_{n=0}^M$ is a sequence in X with zero mean. We define

$$\begin{aligned} \bigl \Vert D^k f_\tau \bigl \Vert _0&= \biggl (\tau \sum _{n=k}^M \bigl \Vert D^k f_n\bigr \Vert ^2\biggr )^{1/2}, \qquad k=1,\ldots ,M, \end{aligned}$$

and, in order to obtain scale invariant constants, for each $k=0,\ldots ,M$,

$$\begin{aligned} \bigl \Vert D^k f_\tau \bigl \Vert _m = \biggl (\sum _{j=k}^{k+m} \frac{1}{T_j^{2(m+k-j)}}\bigl \Vert D^j f_\tau \bigr \Vert _0^2\biggr )^{1/2}, \qquad m=1,\ldots , M-k, \end{aligned}$$

(53)

where, here and in the sequel, $T_0=T$, and

$$\begin{aligned} T_k = (M+1-k) \tau ,\qquad k=1,\ldots ,M. \end{aligned}$$

(54)

We also denote

$$\begin{aligned} m_k=\frac{1}{M+1-k} \sum _{n=k}^M D^kf_n. \end{aligned}$$

(55)

Observe that by applying Hölder’s inequality one gets

$$\begin{aligned} \bigl \Vert m_k\bigr \Vert \le \frac{1}{\sqrt{T_k}} \bigl \Vert D^k f_\tau \bigr \Vert _0 \end{aligned}$$

(56)

On the other hand, it is easy to check $m_k = \min _{\alpha \in {\mathbb {R}}} \left\| D^kf_\tau - \alpha \right\| _0$, where by $D^k f_\tau -\alpha$ we denote the sequence $(D^k f_n -\alpha )_{n=k}^M$. Consequently, for the sequence $D^k f_\tau -m_k = (D^k f_n -m_k)_{n=k}^M$, we have

$$\begin{aligned} \bigl \Vert D^kf_\tau - m_k\bigr \Vert _0 \le \bigl \Vert D^k f_\tau \bigr \Vert _0. \end{aligned}$$

(57)

Our first result extends Lemma 4.1 to the sequences $(D^kf_n)_{n=k}^M$, whose means are not 0.

Lemma 4.7

The following bound holds for $k=1,\ldots M$,

$$\begin{aligned} \bigl \Vert D^k f_n\bigr \Vert \le c_{A,1} \bigl \Vert D^k f_\tau \bigr \Vert _0^{1/2}\bigl \Vert D^k f_\tau \bigr \Vert _1^{1/2},\qquad n=k,\ldots ,M-1, \end{aligned}$$

where

$$\begin{aligned} c_{A,1} = \left( 1 + c_A^{4/3} \right) ^{3/4}, \end{aligned}$$

(58)

and $c_A$ is the constant in (40).

Proof

Applying Lemma 4.1 we have

$$\begin{aligned} \bigl \Vert D^kf_n - m_k\bigr \Vert&\le c_A \bigl \Vert D^kf_\tau - m_k\bigr \Vert _0^{1/2} \bigl \Vert D^{k+1} f_\tau \bigr \Vert _0^{1/2} \nonumber \\& \le {c_A} \bigl \Vert D^kf_\tau \bigr \Vert _0^{1/2} \bigl \Vert D^{k+1} f_\tau \bigr \Vert _0^{1/2}, \end{aligned}$$

(59)

where in the last inequality we have applied (57). Thus, by writing $D^k f_n = D^k f_n -m_k + m_k$ and in view of (56), we have

$$\begin{aligned} \bigl \Vert D^kf_n\bigr \Vert&\le {c_A} \bigl \Vert D^kf_\tau \bigr \Vert _0^{1/2} \bigl \Vert D^{k+1} f_\tau \bigr \Vert _0^{1/2} + T_k^{-1/2}\bigl \Vert D^k f_\tau \bigr \Vert _0 \nonumber \\& = \bigl \Vert D^kf_\tau \bigr \Vert _0^{1/2}\left( {c_A} \bigl \Vert D^{k+1} f_\tau \bigr \Vert _0^{1/2}+ T_k^{-1/2}\bigl \Vert D^k f_\tau \bigr \Vert _0^{1/2}\right) . \end{aligned}$$

Now applying Hölder’s inequality, $ab + cd \le (a^p+c^p)^{\frac{1}{p}} (b^q+d^q)^{\frac{1}{q}}$, to the second factor above, with $p=4/3$ and $q=4$, the proof is finished. $\square$

Next, we extend Lemma 4.4 to the general case

Lemma 4.8

For $k=1,\ldots ,M-1$,

$$\begin{aligned} \bigl \Vert D^kf_\tau \bigr \Vert _0 \le c_{B,1}\bigl \Vert D^{k-1} f_\tau \bigr \Vert _0^{1/2} \bigl \Vert D^{k} f_\tau \bigr \Vert _1^{1/2}, \end{aligned}$$

where

$$\begin{aligned} { c_{B,1} =\left( 2+ 4(c_Ac_{A,1})^2\right) ^{1/2}.} \end{aligned}$$

(60)

Proof

We notice that $D^k f_\tau = D(D^{k-1}f_\tau - m_{k-1})$ and let us denote

$$\begin{aligned} y_n=D^{k-1} f_n -m_{k-1},\qquad n=k-1,\ldots ,M. \end{aligned}$$

Thus, arguing as in the proof of Lemma 4.4 we have

$$\begin{aligned} \bigl \Vert D^k f_\tau \bigr \Vert ^2&=\sum _{n=k}^M (D^k f_n, y_n-y_{n-1}) \nonumber \\& =(D^kf_M,y_M)-(D^kf_k,y_{k-1}) -\sum _{n=k}^{M-1} (D^{k}f_{n+1}-D^k f_n ,y_n) \nonumber \\& =(D^kf_M,y_M)-(D^kf_k,y_{k-1}) -\tau \sum _{n=k}^{M-1} (D^{k+1}f_{n+1} ,y_n). \end{aligned}$$

We apply (59) and Lemma 4.7 to the first two terms on right-hand side above, and we apply (57) to the last one, to get,

$$\begin{aligned} \bigl \Vert D^k f_\tau \bigr \Vert ^2&\le {2c_Ac_{A,1}} \bigl \Vert D^{k-1}f_\tau \bigr \Vert _0^{\frac{1}{2}} \bigl \Vert D^{k} f_\tau \bigr \Vert _0\bigl \Vert D^{k} f_\tau \bigr \Vert _1^{\frac{1}{2}} + \bigl \Vert D^{k-1}f_\tau \bigr \Vert _0 \bigl \Vert D^{k+1}f_\tau \bigr \Vert _0 \nonumber \\ & \le \frac{1}{2} \bigl \Vert D^{k} f_\tau \bigr \Vert _0^2 + {2c_A^2c_{A,1}^2} \bigl \Vert D^{k-1}f_\tau \bigr \Vert _0\bigl \Vert D^{k} f_\tau \bigr \Vert _1 + \bigl \Vert D^{k-1} f_\tau \bigr \Vert _0 \bigl \Vert D^{k+1}f_\tau \bigr \Vert _0. \end{aligned}$$

Thus,

$$\begin{aligned} \bigl \Vert D^k f_\tau \bigr \Vert ^2&\le \bigl \Vert D^{k-1} f_\tau \bigr \Vert _0\left( {4c_A^2c_{A,1}^2}\bigl \Vert D^{k} f_\tau \bigr \Vert _1 +{2}\bigl \Vert D^{k+1}f_\tau \bigr \Vert _0\right) \nonumber \\& \le \bigl \Vert D^{k-1} f_\tau \bigr \Vert _0{\left( 4c_A^2c_{A,1}^2+2\right) }\bigl \Vert D^{k} f_\tau \bigr \Vert _1, \end{aligned}$$

and the proof is finished for $k\ge 2$. $\square$

Lemma 4.9

For $m=2,\ldots ,M$,

$$\begin{aligned} \bigl \Vert D^1f_\tau \bigr \Vert _0 \le c_{m}\bigl \Vert f_\tau \bigr \Vert _0^{\frac{m-1}{m}} \bigl \Vert D^{1} f_\tau \bigr \Vert _{m-1}^{\frac{1}{m}}, \end{aligned}$$

(61)

where

$$\begin{aligned} c_{m} = \prod _{j=0}^{m-2} \hat{c}_j^\frac{1}{j+1}. \end{aligned}$$

(62)

and the constants $\hat{c}_j$ are given in (66) below.

Proof

The result will be a consequence of the following inequality that will be proven below by induction:

$$\begin{aligned} {\bigl \Vert D ^kf_\tau \bigr \Vert _{j} \le \hat{c}_{j} \bigl \Vert D^{k-1}f_\tau \bigr \Vert _{0}^{\frac{1}{j+2}} \bigl \Vert D ^k f_\tau \bigr \Vert _{j+1}^{\frac{j+1}{j+2}}.} \end{aligned}$$

(63)

If (63) holds for $j=0,\ldots ,m-2$, then, applying it successively we have

$$\begin{aligned} \bigl \Vert D ^1f_\tau \bigr \Vert _{0} \le \hat{c}_0 \bigl \Vert f_\tau \bigr \Vert _{0}^{\frac{1}{2}}\bigl \Vert D ^1f_\tau \bigr \Vert _{1}^{\frac{1}{2}}\le & \hat{c}_0\hat{c}_1^{\frac{1}{2}} \bigl \Vert f_\tau \bigr \Vert _{0}^{\frac{1}{2}+\frac{1}{6}}\bigl \Vert D ^1f_\tau \bigr \Vert _{2}^{\frac{1}{3}} \le \ldots \\\le & c_m \bigl \Vert f_\tau \bigr \Vert _{0}^\beta \bigl \Vert D ^1f_\tau \bigr \Vert _{m-1}^{\frac{1}{m}} \end{aligned}$$

where

$$\begin{aligned} \beta =\sum _{j=1}^{m-1} \frac{1}{j(j+1)}=\sum _{j=1}^{m-1}\left( \frac{1}{j} - \frac{1}{j+1}\right) = 1 -\frac{1}{m}= \frac{m-1}{m}, \end{aligned}$$

(64)

so that (61) follows. We now prove (63). Lemma 4.8 shows it holds for $j=0$ with $\hat{c}_0 = c_{B,1}$. Let us assume that it holds for $j=0,\ldots ,m-2$, and let us show that it holds for $m-1$. We do this for $k=1$ since the argument is the same for $k>1$. We notice

$$\begin{aligned} \bigl \Vert D ^1f_\tau \bigr \Vert _{m-1} = \left( T^{-2(m-1)}\bigl \Vert D ^1f_\tau \bigr \Vert _{0}^2 +\bigl \Vert D ^2f_\tau \bigr \Vert _{m-2}^2 \right) ^{\frac{1}{2}} \end{aligned}$$

and apply the induction hypotheses to the second term on the right-hand side above to get

$$\begin{aligned} \bigl \Vert D ^1f_\tau \bigr \Vert _{m-1}&\! =\! \left( T^{-2(m-1)}\bigl \Vert D ^1f_\tau \bigr \Vert _{0}^2 +\hat{ {c}}_{m-2}^2\bigl \Vert D ^1f_\tau \bigr \Vert _{0}^{\frac{2}{m}} \bigl \Vert D ^2f_\tau \bigr \Vert _{m-1}^{\frac{2(m-1)}{m}} \right) ^{\frac{1}{2}} \nonumber \\& \! =\! \bigl \Vert D ^1f_\tau \bigr \Vert _{0}^{\frac{1}{m}} \!\left( T^{-2(m-1)}\bigl \Vert D ^1f_\tau \bigr \Vert _{0}^{\frac{2(m-1)}{m}} \!+\hat{ {c}}_{m-2}^2 \bigl \Vert D ^2f_\tau \bigr \Vert _{m-1}^{\frac{2(m-1)}{m}} \right) ^{\frac{1}{2}} \nonumber \\& \! =\! AB. \end{aligned}$$

Now, we use that, as argued above, the induction hypothesis implies that (61) holds, so that we can write

$$\begin{aligned} \bigl \Vert D ^1f_\tau \bigr \Vert _{m-1}&= c_m^{\frac{1}{m}} \bigl \Vert f_\tau \bigr \Vert _0^{\frac{m-1}{m^2}} \bigl \Vert D ^1f_\tau \bigr \Vert _{m-1}^{\frac{1}{m^2}} B, \end{aligned}$$

so that, dividing by $\bigl \Vert D ^1f_\tau \bigr \Vert _{m-1}^{\frac{1}{m^2}}$ we have

$$\begin{aligned} \bigl \Vert D ^1f_\tau \bigr \Vert _{m-1}^{\frac{m^2-1}{m^2}}&= c_m^{\frac{1}{m}} \bigl \Vert f_\tau \bigr \Vert _0^{\frac{m-1}{m^2}} B, \end{aligned}$$

which implies

$$\begin{aligned} \bigl \Vert D ^1f_\tau \bigr \Vert _{m-1}&= c_m^{\frac{m}{m^2-1}} \bigl \Vert f_\tau \bigr \Vert _0^{\frac{1}{m+1}} B^{\frac{m^2}{m^2-1}}. \end{aligned}$$

(65)

Now we apply Holder’s inequality $ab+cd \le (a^p+c^p)^{1/p}(b^q+d^q)^{1/q}$ to B, with $p=m$ and $q=m/(m-1)$

$$\begin{aligned} B&\le \left( 1+\hat{ {c}}_{m-2}^{2m}\right) ^{\frac{1}{2m}} \left( T^{-2m}\bigl \Vert D ^1f_\tau \bigr \Vert _{0}^{2}+ \bigl \Vert D ^2f_\tau \bigr \Vert _{m-1}^2 \right) ^{\frac{m-1}{2m}} \nonumber \\& = \left( 1+\hat{ {c}}_{m-2}^{2m}\right) ^{\frac{1}{2m}} \bigl \Vert D^1 f_\tau \bigr \Vert _m^{\frac{m-1}{m}}, \end{aligned}$$

which, together with (65), implies

$$\begin{aligned} \bigl \Vert D ^1f_\tau \bigr \Vert _{m-1} = \left( \left( 1+\hat{ {c}}_{m-2}^{2m}\right) c_m^2\right) ^{\frac{m}{2(m+1)(m-1)}} \bigl \Vert f_\tau \bigr \Vert _0^{\frac{1}{m+1}}\bigl \Vert D^1 f_\tau \bigr \Vert _m^{\frac{m}{m+1}}. \end{aligned}$$

This is (63) for $j=m-1$ with

$$\begin{aligned} \hat{c}_j = \left( 1+\hat{{c}}_{j-1}^{2(j+1)}\right) ^{\frac{j+1}{2(j+2)j}} \biggl (\prod _{i=0}^{j-1} \hat{c}_i^{\frac{1}{i+1}}\biggr )^{\frac{j+1}{(j+2)j}},\qquad \hat{c}_0={c_{B,1}}, \end{aligned}$$

(66)

where $c_{B,1}$ is the constant given in (60). $\square$

Table 7 shows the first 5 values of $c_m$ for $c_A$ given by (48). Computation of further values suggests that $c_m\approx \gamma ^{m-1}$ with $\gamma =5.9416$.

From Lemmas 4.1 and 4.9 the following result follows.

Lemma 4.10

Let $f_\tau =(f_n)_{n=0}^M$ a sequence in X with zero mean. Then, for $m=1,\ldots ,M-1$, the following estimate holds:

$$\begin{aligned} \bigl \Vert f_n\bigr \Vert \le c_Ac_m^{\frac{1}{2}}\bigl \Vert f_\tau \bigr \Vert _0^{1-\frac{1}{2m}} \bigl \Vert D^1f_\tau \bigr \Vert _{m-1}^{\frac{1}{2m}}, \end{aligned}$$

(67)

where $c_A$ is the constant in (40) (or (48) for X being a space of functions or ${\mathbb {R}}^N$) and $c_m$ is $c_m=1$ if $m=1$ and the constant in (62) for $m\ge 2$.

4.3 Application to Sequences of Function Values

We consider now the case where X is either $L^2(\Omega )$ or some Sobolev space $H^s(\Omega )$ for some domain $\Omega \subset {\mathbb {R}}^d$, $\left\| \cdot \right\|$ its norm, and $f_n=f(\cdot , t_n)$ for some function $f:\Omega \times [0,T] \rightarrow {\mathbb {R}}$ such that $f\in H^m(0,T,X)$. We first notice that since for $x\in \Omega$ we have $D^{k-1} f(x,t_n) =\partial ^{k-1} f(x,\xi )$ for some $\xi \in (t_{n-k+1},t_n)$, then it follows that

$$\begin{aligned} \bigl \Vert D^kf_n\bigr \Vert \le \frac{\sqrt{k}}{\sqrt{\tau }} \bigl \Vert \partial ^kf\bigr \Vert _{L^2(t_{n-k},t_n,X)},\qquad k\le n\le M. \end{aligned}$$

(68)

Consequently,

$$\begin{aligned} \bigl \Vert D^kf_\tau \bigr \Vert _0 \le k\bigl \Vert \partial ^kf\bigr \Vert _{L^2(0,T,X)}. \end{aligned}$$

(69)

We have the following result.

Theorem 4.11

Let $f:X\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ a function which is T-periodic in its last variable and such that $f\in H^m(0,T,X)$. Then, the sequence $f_\tau =(f_n)_{n=1}^M$ satisfies the following bounds for $1\le m\le M-1$:

$$\begin{aligned} \bigl \Vert Df_\tau \bigr \Vert _0&\le 2^{\frac{m-1}{m}}m^{\frac{1}{m}}\left\| f_\tau \right\| _0^{\frac{m-1}{m}} \left\| \partial ^m f\right\| _{L^2(0,T,X)}^{\frac{1}{m}}, \nonumber \\ \bigl \Vert f_n\bigr \Vert&\le 2^{\frac{m-1}{2m}}m^{\frac{1}{2m}}c_A\left\| f_\tau \right\| _0^{1-\frac{1}{2m}} \left\| \partial ^m f\right\| _{L^2(0,T,X)}^{\frac{1}{2m}} +\frac{1}{\sqrt{T}}\bigl \Vert f_\tau \bigr \Vert _0, \quad 1\le n\le M, \end{aligned}$$

where $c_m$ is the constant in Lemma 4.10. If $f_1+\cdots +f_M=0$, the the last term on the right-hand side above can be omitted.

Proof

Let us denote $m_0=(f_1+\cdots +f_M)/M$. Applying Hölder’s inequality is easy to check that $\left| m_0\right| \le T^{-1/2}\bigl \Vert f_\tau \bigr \Vert _0$ and, consequently, $\left\| f_\tau -m_0\right\| _0 \le 2\left\| f_\tau \right\| _0$. Thus, by expressing $f_n=(f_n-m_0)+m_0$, applying Lemmas 4.5 and 4.6 to $f_\tau - m_0$ and using (69) the result follows for $m\ge 2$. For $m=1$ the result follows form Lemma 4.6 and (69). $\square$

For the general case, in view of the definition of $\bigl \Vert D^k f_\tau \bigl \Vert _m$ in (53) and (69) we have

$$\begin{aligned} \bigl \Vert D f_\tau \bigr \Vert _{m-1}^{\frac{1}{m}}&\!\le \! \biggl ( \sum _{k=0}^{m-1} (k+1)^2\left( \frac{T}{T_{k+1}}\right) ^{2(m-k)} \!\!\! \frac{1}{T^{2(m-k)}}\bigl \Vert \partial _t^{k+1} f\bigr \Vert _{L^2(0,T,X)}^2\biggr )^{\frac{1}{2m}} \nonumber \\& \!\le \! \max _{0\le k \le m-1} (k+1)^{\frac{1}{m}}\left( \frac{T}{T_{k+1}}\right) ^{\frac{m-k}{m}} \bigl \Vert \partial _tf\bigr \Vert _{H^{m-1}(0,T,X)}^{\frac{1}{m}}, \end{aligned}$$

(70)

where $\left\| \cdot \right\| _{H^{m-1}(0,T,X)}$ is defined in (1). We now estimate the maximum above. In view of the expression of $T_k$ in (54), for $1\le k\le m-1$ we have

$$\begin{aligned} & \left( \frac{T}{T_{k+1}}\right) ^{\frac{m-k}{m}} =\left( \frac{M}{M-k}\right) ^{\frac{m-k}{m}} = \left( 1 +\frac{k}{M-k}\right) ^{\frac{m-k}{m}} = \left( 1 +\frac{1}{(M/k)-1}\right) ^{\frac{m-k}{m}} \\ & =\left( \left( 1 +\frac{1}{(M/k)-1}\right) ^{(M/k)-1}\right) ^{\frac{m-k}{m((M/k)-1)}} \le e^{\frac{m-k}{m((M/k)-1)}} = e^{\frac{k(m-k)}{m(M-k)}}. \end{aligned}$$

Now the function $x\mapsto x(m-x)/(m(M-x))$ is monotone increasing in the interval $[1,m-1]$, unless $m\le M/4$ where it has a relative maximum at $(M/2)-\sqrt{(M^2/4)-Mm}$, but is easy to check that this value is strictly larger than m. Consequently, its maximum is achieved at $x=m-1$. Noticing that $x^{1/x} \le e^{\frac{1}{e}}$ for $x>0$, we conclude that, for $2\le m\le M$

$$\begin{aligned} \max _{0\le k \le m-1} (k+1)^{\frac{1}{m}}\left( \frac{T}{T_{k+1}}\right) ^{\frac{m-k}{m}} \le e^{\frac{m-1}{m(M-m+1)}+\frac{1}{e}}\le e^{1+\frac{1}{e}}. \end{aligned}$$

One can check that $e^{1+\frac{1}{e}}\le 3.93$. Thus, from (70) it follows that

$$\begin{aligned} \bigl \Vert D^{1} f_\tau \bigr \Vert _{m-1}^{\frac{1}{m}} \le 4 \bigl \Vert \partial _tf\bigr \Vert _{H^{m-1}(0,T,X)}^{\frac{1}{m}}. \end{aligned}$$

(71)

Theorem 4.12

Let $f\in H^m(0,T,X)$. Then, the sequence $f_\tau =(f_n)_{n=0}^M$ satisfies the following bound for $1\le m\le M$:

$$\begin{aligned} \bigl \Vert D^1 f_\tau \bigr \Vert&\le 2^{\frac{m-1}{m}}c_m \left\| f_\tau \right\| _0^{\frac{m-1}{m}} \left\| \partial _t f\right\| _{H^{m-1}(0,T,X)}^{\frac{1}{m}}, \end{aligned}$$

(72)

$$\begin{aligned} \bigl \Vert f_n\bigr \Vert&\le 2^{\frac{m-1}{2m}} c_Ac_m^{1/2} \bigl \Vert f_\tau \bigr \Vert _0^{1-\frac{1}{2m}} \left\| \partial _t f\right\| _{H^{m-1}(0,T,X)}^{\frac{1}{2m}} +\frac{1}{\sqrt{T}}\bigl \Vert f_\tau \bigr \Vert _0, \nonumber \\&n=0,\ldots ,M. \end{aligned}$$

(73)

If $f_0+\cdots +f_M=0$, the last term on the right-hand side above can be omitted.

Proof

Let us denote $m_0=(f_0+\cdots +f_M)/(M+1)$. Applying Hölders inequality one sees that $\left| m_0\right| \le T^{-1/2}\bigl \Vert f_\tau \bigr \Vert _0$ so that $\left\| f_\tau -m_0\right\| _0 \le 2\left\| f_\tau \right\| _0$. Thus, by writing $f_n=(f_n-m_0)+m_0$, applying Lemmas 4.9 (if $m\ge 2$) and 4.10 to $f_\tau - m_0$ and using (71) the proof is finished. $\square$

5 Summary and Conclusions

Several estimates, pointwise and averaged, have been proved for POD methods whose data set does not include DQs of the snapshots. These estimates include pointwise projection errors of snapshots (Theorems 2.1 and 2.2 in the general case and estimate (8) in the case of periodic functions in time) for orthogonal projections in $L^2$ and $H^1_0$. They also include $L^2$ norm of $H^1_0$-projection errors (estimate (11)), for which estimate (10) has been used. Our estimates also include (the square root of) the average of squared projection error of DQs (Theorem 2.3 for the general case and estimate (9) for periodic functions) again in the $L^2$ and $H^1_0$ cases, as well as the average of squares of $L^2$ norms of Ritz projection errors of DQs (estimate (12)). In all cases, when projections are onto the space spanned by the first r elements of the POD basis, the rate of decay in terms of $\sigma _{r+1}^2 + \cdots +\sigma _J^2$ is as close to the optimal value $(\sigma _{r+1}^2 +\cdots + \sigma _J^2)^{1/2}$ as the smoothness of the function from where the snapshots are taken allows.

These estimates have been used to obtain error bounds with the same rates of decay for POD methods applied to the heat equation, where both backward Euler method and the BDF2 are considered for discretization of the time variable (Theorem 2.6). The heat equation has been chosen for simplicity, but it is clear that, with techniques for nonlinear problems such as those, for example, in [5, 7, 9, 13, 16], it is possible to extend these estimates to POD methods not using DQs in the data set for nonlinear equations.

Numerical experiments are also presented in this paper, where snapshots are taken from two challenging problems due to the size of derivatives with respect to time (see Fig. 1) and Table 4), derivatives which feature in the estimates commented above. In these experiments, pointwise projection errors are overestimated by our error bounds by factors not exceeding 28, and by a factor also not exceeding 28 in the case of the (square root of) the average of squares of $L^2$ norms of Ritz projection errors of DQs, if the estimates are those in Remark 2.7, although these factors are likely to be problem-dependent.

This research was motivated by a better understanding of POD methods that do not include DQs of the snapshots in the data set. In particular by the apparent contradiction that while counterexamples in [12] clearly show that pointwise projection errors do degrade with the number of snapshots, computations like those in Table 1 suggest that this may not necessarily be the case in practice. By taking into account the smoothness of functions from where the snapshots are taken, new estimates have been obtained and the apparent contradiction mentioned above has been explained, as well as better knowledge of the decay rate of pointwise errors when DQs are omitted from the data set.