1 Introduction

The use of the discontinuous Galerkin method (dG) is growing, see for example [10, 14], and over recent decades it has become one of the dominant approach for solving some classes of partial differential equations (PDEs). In this method, the approximation polynomials can be modal (cell-based), and the cells can have complex shapes as long as one can integrate polynomials over these cells and their faces, which provides the method with greater flexibility. Consequently, the use of polygonal meshes in 2D and polyhedral meshes in 3D is on the rise, see [10, 16], a typical goal is to have a mesh that faithfully captures the input domain geometry. The integration of a polynomial over a mesh element is a crucial and indispensable step in dG method. When the elements have complex shapes, the computation of these integrals becomes challenging. The literature on this subject is extensive and remains active, as evidenced by recent publications. In this work, we propose a method that is both easy to understand and straightforward to implement.

In [10, Chapter 6], one can find the state of the art of polynomial integration methods over polygons and polyhedra, see also [23]. The methods used in the literature for calculating these integrals fall into three main categories:

  1. i)

    The first category consists in partitioning the domain of integration \(D\) with a tessellation of a finite number of simple elements, such as tetrahedra, and calculating the integrals over each of these individual elements, see [1].

  2. ii)

    The second category uses quadrature formulas to compute these integrals, see [2, 17, 20,21,22,23].

  3. iii)

    The third category is based on the generalized Stokes’ theorem to convert volume integrals into surface integrals, as seen in [11, 12, 18, 19, 21]. The method we propose here falls within the scope of this category, although our approach differs from those in the references mentioned above.

The authors in [11] propose a method for integrating positively homogeneous functions over polygons and polyhedra, using Euler’s formula. Recall that a function f(x) is said to be positively homogeneous of degree q if: \( f(\lambda x) = \lambda ^q \ f(x)\), for all \(\lambda >0\), which satisfies Euler’s homogeneous function theorem: \(q f (x) = x \cdot \nabla f(x)\). Monomials are homogeneous functions, and thus the proposed approach allows the integration of polynomials over polygons and polyhedra.

In 2D geometries, polynomial integration over arbitrary polygons can be performed exactly when the polygon edges are either line segments or circular arcs, as shown in [8]. The approach used in [8] for polygons was extended in [3, 4] to extruded 2D cells of the form \(S \times [z_0, z_1]\), where S is a polygon. In this document, we extend the approach of [8] for 2D polygonal meshes to handle 3D polyhedral meshes with arbitrary shapes. Our method differs from that in [11] and is more general, allowing the integration of functions that are not necessarily homogeneous. While both approaches employ Stokes’ theorem, but with two different versions. Indeed, here we use Stokes’ theorem in its classical form, also known as curl theorem [9, page 294], converting the surface integral of the curl of a vector field \({\textbf{G}}\) into a line integral over the boundary of the surface:

$$\begin{aligned} \int _S (\mathbf{{\nabla }}\times {\textbf{G}}) \cdot {\hat{{\varvec{n}}}}\ \textrm{d}s = \oint _{\partial S} {\textbf{G}}\cdot \textrm{d}\textbf{r}, \end{aligned}$$

where the symbol \(\times \) represents the cross product, \({\hat{{\varvec{n}}}}\) is the unit normal vector to the surface S, \(\textrm{d}s\) represents the infinitesimal surface area element, \(\partial S\) denotes the closed boundary of S oriented positively according to Stokes’ theorem, using the right hand rule, and \( \textrm{d}\textbf{r}\) is the infinitesimal vector element along the curve \(\partial S\).

Whereas in [11], they use the generalized version of Stokes’ theorem, which is expressed for a vector field \({\textbf{G}}(x)\) and a function f(x) as:

$$\begin{aligned} \int _D(\mathbf{{\nabla }}\cdot {\textbf{G}}) f(x) \textrm{d}x + \int _D{\textbf{G}}\cdot \mathbf{{\nabla }}f(x) \textrm{d}x = \int _{\partial D} ({\textbf{G}}\cdot {\hat{{\varvec{n}}}}) f(x) \textrm{d}s. \end{aligned}$$

In [11], the above equation is applied whether D represents a volume region, a surface, or curved line.

2 Notations and Definitions

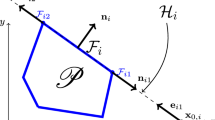
In this section, we introduce the notations, definitions, and assumptions useful throughout the paper. Let \(D\) be an open and bounded region in \({\mathbb {R}}^3\), not necessarily convex. We denote its boundary by \(\partial D\), assumed to be piecewise smooth, so that the unit normal vector \({\hat{{\varvec{n}}}}= ({\hat{{\varvec{n}}}}_x, {\hat{{\varvec{n}}}}_y, {\hat{{\varvec{n}}}}_z)\) to the boundary \(\partial D\), oriented outward from \(D\), is well-defined almost everywhere in the sense of the Lebesgue measure \(\textrm{d}s\) on the surface \(\partial D\).

In other words, \(D\) is an arbitrary polyhedron whose boundary \(\partial D\) can be decomposed into a finite number of faces that are not necessarily flat and are pairwise disjoint. We denote the finite set of these faces by \({\mathbb {F}}\), so:

$$\begin{aligned} \partial D= \bigcup _{{\mathcal {F}}\in {\mathbb {F}}} {\mathcal {F}}. \end{aligned}$$

This partitioning of \(\partial D\) into faces \({\mathcal {F}}\) can be viewed as a mesh of the surface \(\partial D\), not necessarily conforming (potentially including hanging nodes), where each face \({\mathcal {F}}\) is an element of the mesh. The faces \({\mathcal {F}}\in {\mathbb {F}}\) are assumed to have non-zero measure, to be smooth enough, and not necessarily flat, with the outward normal vector \({\hat{{\varvec{n}}}}\) defined everywhere on each face \({\mathcal {F}}\). Thus, the only irregularities allowed on the surface \(\partial D\) occur at the intersections of two faces in \({\mathbb {F}}\).

The boundary \(\partial {\mathcal {F}}\) of each face \({\mathcal {F}}\in {\mathbb {F}}\) will be divided into a finite number of edges \({\mathcal {E}}\), each with non-zero measure and pairwise disjoint. The set of these edges will be denoted by \({\mathbb {E}}({\mathcal {F}})\):

$$\begin{aligned} \partial {\mathcal {F}}= \bigcup _{{\mathcal {E}}\in {\mathbb {E}}({\mathcal {F}})} {\mathcal {E}}. \end{aligned}$$

For each face \({\mathcal {F}}\in {\mathbb {F}}\), we assume that all its edges \({\mathcal {E}}\in {\mathbb {E}}({\mathcal {F}})\) are smooth, i.e., each edge can be parameterized by a simple path \(\gamma \):

$$\begin{aligned} \gamma = \gamma ({\mathcal {E}}, {\mathcal {F}}): {\left\{ \begin{array}{ll} \ [a,b] \ \longrightarrow {\mathcal {E}}\\ \quad \quad t \ \longmapsto (x(t), y(t), z(t)), \end{array}\right. } \end{aligned}$$
(1)

where a and b are real numbers, and x(t), y(t) et z(t) are \({\mathcal {C}}^1\) functions. The values a, b, x(t), y(t) and z(t) depend on the face \({\mathcal {F}}\) and the edge \({\mathcal {E}}\).

The boundary \(\partial {\mathcal {F}}\) of each face \({\mathcal {F}}\) is a closed curve assumed to be oriented positively, following the direction prescribed by Stokes’ theorem. Similarly, each edge \({\mathcal {E}}\in {\mathbb {E}}({\mathcal {F}})\) is considered to be oriented consistently with the closed curve \(\partial {\mathcal {F}}\).

In this document, we focus on how to integrate a smooth function f(x, y, z) over a domain \(D\) as described above. The case where f is a polynomial and the domain \(D\) is a classical polyhedron with flat faces and straight edges is essential in the discontinuous finite element method. This specific case will be analyzed in Sect. 5.2.

The purpose of this work is therefore to explain how to calculate the integral:

$$\begin{aligned} I(D,f) = \int _Df(x,y,z) \ \textrm{d}x \textrm{d}y \textrm{d}z. \end{aligned}$$
(2)

To do so, we proceed in three steps:

  1. 1.

    The first step reduces the volume integral over \(D\) to a surface integral over \(\partial D\), and therefore over the faces \({\mathcal {F}}\in {\mathbb {F}}\), by applying the divergence theorem, Sect. 3.

  2. 2.

    The second step further reduces each surface integral over a face \({\mathcal {F}}\in {\mathbb {F}}\) to a line integral over its boundary \(\partial {\mathcal {F}}\), and thus over the edges \({\mathcal {E}}\in {\mathbb {E}}({\mathcal {F}})\), using Stokes’ theorem, Sect. 4.

  3. 3.

    The final step involves computing the line integrals by parameterizing the edge \({\mathcal {E}}\) along which the integration is carried out, Sect. 5. Additionally, Sect. 6 introduces an alternative method for evaluating these line integrals using the gradient theorem.

3 Volume Integral

Consider a \({\mathcal {C}}^1\) function f(x, y, z) defined in \({\mathbb {R}}^3\) with values in \({\mathbb {R}}\), for which we want to calculate the integral (2). To do this, we start by defining the vector field \({\textbf{F}}\) as:

$$\begin{aligned} {\textbf{F}}(x,y,z) = (0, \ 0, \ f^\star (x,y,z)), \end{aligned}$$
(3)

where \(f^\star (x,y,z)\) is an antiderivative of f with respect to the z variable, in other words:

$$\begin{aligned} \partial _z f^\star (x,y,z) = f(x,y,z), \end{aligned}$$
(4)

\(\partial _z\) being the partial derivative with respect to the z variable. Since the function f is assumed to be \({\mathcal {C}}^1\), the above equation (4) is well-defined.

Proposition 1

Then we have:

$$\begin{aligned} I(D,f) = \int _Df(x,y,z) \ \textrm{d}x \textrm{d}y \textrm{d}z = \int _{\partial D} {\textbf{F}}\cdot {\hat{{\varvec{n}}}}\ \textrm{d}s = \sum _{{\mathcal {F}}\in {\mathbb {F}}} \int _{{\mathcal {F}}} {\textbf{F}}\cdot {\hat{{\varvec{n}}}}\ \textrm{d}s, \end{aligned}$$
(5)

where \({\textbf{F}}\) is the vector field defined by (3) and \({\hat{{\varvec{n}}}}\) is the unit normal vector pointing outward at the boundary \(\partial D\).

Proof

The field \({\textbf{F}}\) was chosen to satisfy the equation: \( f(x,y,z) = \textrm{div}\ {\textbf{F}}(x,y,z)\). Thus, by the divergence theorem, we get:

$$\begin{aligned} \int _Df(x,y,z) \ \textrm{d}x \textrm{d}y \textrm{d}z = \int _D\textrm{div}\ {\textbf{F}}\ \textrm{d}x \textrm{d}y \textrm{d}z = \int _{\partial D} {\textbf{F}}\cdot {\hat{{\varvec{n}}}}\ \textrm{d}s. \end{aligned}$$

This gives the result stated in the proposition. \(\square \)

Thus, the volume integral \(I(D,f)\) reduces to calculating surface integrals over each of the faces \({\mathcal {F}}\in {\mathbb {F}}\):

$$\begin{aligned} I({\mathcal {F}}, {\textbf{F}}) = \int _{{\mathcal {F}}} {\textbf{F}}\cdot {\hat{{\varvec{n}}}}\ \textrm{d}s. \end{aligned}$$
(6)

4 Surface Integral

In this section, we explain how to calculate the surface integrals \(I({\mathcal {F}}, {\textbf{F}})\) defined by (6). To do this, let us first make two remarks:

Remark 1

When the face \({\mathcal {F}}\) is parallel to the z-axis and not necessarily flat, i.e., \({\mathcal {F}}\) is a vertical face, the component \({\hat{{\varvec{n}}}}_z\) of the normal to the face \({\mathcal {F}}\) is zero (\({\hat{{\varvec{n}}}}_z =0\)). And consequently, \( I({\mathcal {F}}, {\textbf{F}}) = 0\) because \({\textbf{F}}\cdot {\hat{{\varvec{n}}}}= 0\). This means that vertical faces \({\mathcal {F}}\) do not contribute to the integral (5).

Remark 2

When a face \({\mathcal {F}}\) can be decomposed into two sub-faces, one vertical \({\mathcal {F}}_0\) (\({\hat{{\varvec{n}}}}_z =0\)) and the other not \({\mathcal {F}}_1\) (\({\hat{{\varvec{n}}}}_z \ne 0\)), then the sub-face \({\mathcal {F}}_0\) does not contribute to the integral (5), for the same reason mentioned earlier in Remark 1. In practical cases, this decomposition of a face into two does not arise; it is mentioned here only for mathematical rigor, as no assumptions are made about the shapes of the polyhedron’s faces.

The two above remarks allow us to exclude vertical faces or portions of vertical faces from the integral (5). Thus, from now on, we will assume that the \({\hat{{\varvec{n}}}}_z\) component is nonvanishing on the considered face \({\mathcal {F}}\). Consequently, we can express z as a function of x and y for points (x, y, z) belonging to the face \({\mathcal {F}}\):

$$\begin{aligned} z = g^{{\mathcal {F}}}(x,y), \quad \forall (x,y,z) \in {\mathcal {F}}. \end{aligned}$$
(7)

The function \(g^{{\mathcal {F}}}(x,y)\) describing the face \({\mathcal {F}}\) is assumed to be \({\mathcal {C}}^1\) and given by an explicit expression.

To explain equation (7), let us express the surface \({\mathcal {F}}\) by \(h(x,y,z) = 0\), where the function h is \({\mathcal {C}}^1\). The normal vector to the face \({\mathcal {F}}\) is given by \(\nabla h\), the gradient of h, whose component along the z-axis is \(\partial _z h\). Since the component \({\hat{{\varvec{n}}}}_z\) of the normal vector along the z-axis is assumed to be non-zero, we have \(\partial _z h \ne 0\). The implicit function theorem, see [25, page 14], then ensures that the equation \(h(x,y,z) = 0\) for the surface \({\mathcal {F}}\) can be expressed locally in the form (7). In practice, when \({\hat{{\varvec{n}}}}_z \ne 0\) the face \({\mathcal {F}}\) can be described globally by (7) and not just locally. For instance, if the face \({\mathcal {F}}\) is flat and non-vertical, equation (7) would be written as \(z = g^{{\mathcal {F}}}(x,y) = \alpha x+ \beta y+ \kappa \), where \(\alpha \), \(\beta \) and \(\kappa \) are real constants, this will be detailed further in Sect. 5.1. In pathological cases where equation (7) holds only piecewise on \({\mathcal {F}}\), the integral over \({\mathcal {F}}\) must be computed separately for each piece.

Before stating the proposition summarizing the desired result, we start by defining the vector field \({\textbf{G}}^{{\mathcal {F}}}\) as:

$$\begin{aligned} {\textbf{G}}^{{\mathcal {F}}}(x,y,z) = (0, \ Q^{{\mathcal {F}}}(x,y), \ 0), \end{aligned}$$
(8)

and where the function \(Q^{{\mathcal {F}}}\) depends only on x and y, and is such that:

$$\begin{aligned} \partial _x Q^{{\mathcal {F}}}(x,y) = f^\star (x,y,g^{{\mathcal {F}}}(x,y)), \end{aligned}$$
(9)

where \(\partial _x\) is the partial derivative with respect to the x variable, thus \(Q^{{\mathcal {F}}}\) is an antiderivative of \(f^\star (x,y,g^{{\mathcal {F}}}(x,y))\) with respect to the x variable. This choice of the vector field \({\textbf{G}}^{{\mathcal {F}}}\) will become clear in the proof of the following proposition.

Proposition 2

Let \( \textrm{d}\textbf{r}\) denote the Lebesgue measure along the boundary \(\partial {\mathcal {F}}\) of \({\mathcal {F}}\), and orient the closed curve \(\partial {\mathcal {F}}\) positively, that is, following the direction prescribed by Stokes’ theorem. Then we have:

$$\begin{aligned} I({\mathcal {F}}, {\textbf{F}}) = \int _{{\mathcal {F}}} {\textbf{F}}\cdot {\hat{{\varvec{n}}}}\ \textrm{d}s = \oint _{\partial {\mathcal {F}}} {\textbf{G}}^{{\mathcal {F}}}\cdot \textrm{d}\textbf{r}= \sum _{{\mathcal {E}}\in {\mathbb {E}}({\mathcal {F}})} \int _{{\mathcal {E}}} {\textbf{G}}^{{\mathcal {F}}}\cdot \textrm{d}\textbf{r}. \end{aligned}$$
(10)

Proof

Since on the face \({\mathcal {F}}\) we have \(z=g^{{\mathcal {F}}}(x,y)\), the vector field \({\textbf{F}}\) (3) can be written on the face \({\mathcal {F}}\) as:

$$\begin{aligned} {\textbf{F}}(x,y,z) = (0,\ 0, \ f^\star (x,y,g^{{\mathcal {F}}}(x,y))), \quad \forall (x,y,z) \in {\mathcal {F}}. \end{aligned}$$

The vector field \({\textbf{G}}^{{\mathcal {F}}}\) (8) is chosen to satisfy the following equation:

$$\begin{aligned} {\textbf{F}}= \mathbf{{\nabla }}\times {\textbf{G}}^{{\mathcal {F}}}, \quad \forall (x,y,z) \in {\mathcal {F}}. \end{aligned}$$
(11)

The above equation is easy to verify by observing that \(\partial _z Q^{{\mathcal {F}}}= 0\), this allows us to write by combining (6) and (11):

$$\begin{aligned} I({\mathcal {F}}, {\textbf{F}}) = \int _{{\mathcal {F}}} {\textbf{F}}\cdot {\hat{{\varvec{n}}}}\ \textrm{d}s = \int _{{\mathcal {F}}} (\mathbf{{\nabla }}\times {\textbf{G}}^{{\mathcal {F}}}) \cdot {\hat{{\varvec{n}}}}\ \textrm{d}s. \end{aligned}$$

So, the result stated in equation (10) follows immediately from the classical Stokes’ theorem. \(\square \)

Corollary 1

The integral of the function f over D can be written:

$$\begin{aligned} \int _Df(x,y,z) \ \textrm{d}x \textrm{d}y \textrm{d}z = \sum _{{\mathcal {F}}\in {\mathbb {F}}} \ \sum _{{\mathcal {E}}\in {\mathbb {E}}({\mathcal {F}})} \int _{{\mathcal {E}}} {\textbf{G}}^{{\mathcal {F}}}\cdot \textrm{d}\textbf{r}. \end{aligned}$$
(12)

Proof

The result stated in the corollary is an immediate consequence of Propositions 1 and 2. \(\square \)

Remark 3

It is worth noting that in the case where the edge \({\mathcal {E}}\) is perpendicular to the y-axis, then \( {\textbf{G}}^{{\mathcal {F}}}\cdot \textrm{d}\textbf{r}= 0\), and consequently \(I({\mathcal {E}}, {\mathcal {F}}) =\int _{{\mathcal {E}}} {\textbf{G}}^{{\mathcal {F}}}\cdot \textrm{d}\textbf{r}= 0\). This implies that edges perpendicular to the y-axis do not contribute to the integrals (10) and (12).

The above equation (12) reduces the volume integral over the polyhedron \(D\) to line integrals along its edges. It should be noted that equation (12) is exact and no approximation has been used at this stage. For each non-vertical face \({\mathcal {F}}\) and for each edge \({\mathcal {E}}\in {\mathbb {E}}({\mathcal {F}})\), the following integral still remains to be computed:

$$\begin{aligned} I({\mathcal {E}}, {\mathcal {F}}) = \int _{{\mathcal {E}}} {\textbf{G}}^{{\mathcal {F}}}\cdot \textrm{d}\textbf{r}, \end{aligned}$$
(13)

where the edge \({\mathcal {E}}\) may be a curved line.

Equation (12), together with remarks 1 and 3, forms the cornerstone for calculating the desired integrals, particularly when the equations describing the surfaces and edges, as well as the integrand, are well-behaved. For instance, in cases where all these functions are polynomials, the integrals can be computed exactly.

Remark 4

In equation (8), the vector field \({\textbf{G}}^{{\mathcal {F}}}\) was chosen to be parallel to the y-axis. It could also have been chosen along the x-axis: \({\textbf{G}}^{{\mathcal {F}}}(x,y,z) = (Q^{{\mathcal {F}}}(x,y), \ 0, \ 0)\), by replacing equation (9) with \(\partial _y Q^{{\mathcal {F}}}(x,y) = - f^\star (x,y,g^{{\mathcal {F}}}(x,y))\).

5 Line Integral

The integral (13) can be calculated by parameterizing the edge \({\mathcal {E}}\), considering the path \(\gamma = \gamma ({\mathcal {E}}, {\mathcal {F}})\) given by (1), so \( \textrm{d}\textbf{r}= \left( x^\prime (t), y^\prime (t), (z^\prime (t) \right) \textrm{d}t\). Thus, the integral (13) can be written:

$$\begin{aligned} I({\mathcal {E}}, {\mathcal {F}}) = \int _a^b Q^{{\mathcal {F}}}\left( x(t), y(t) \right) \ y^\prime (t) \ \textrm{d}t, \end{aligned}$$
(14)

where \(Q^{{\mathcal {F}}}(x,y)\), see (9), is an antiderivative of the function \(f^\star (x,y,g^{{\mathcal {F}}}(x,y))\) with respect to the variable x. This integral depends on the expressions of the functions f and \(g^{{\mathcal {F}}}\), because \(Q^{{\mathcal {F}}}\) depends on them. It also depends on the shape of the edge \({\mathcal {E}}\), as the path \(\gamma \) varies accordingly. Generally, this integral cannot be solved analytically; however, it can be approximated using quadrature methods such as Gaussian quadrature or the trapezoidal rule. Nevertheless, in specific case, such as when the face \({\mathcal {F}}\) is flat, the edge \({\mathcal {E}}\) is a straight line segment and the function f is a polynomial, this integral can be evaluated exactly, as we will discuss in the following sections.

5.1 Line Integral in the Case Where the Edge is a Line Segment

In this section, we propose to develop the calculation of the integral (14) in the case where the face \({\mathcal {F}}\) is flat and the edge \({\mathcal {E}}\) is a line segment, with the face \({\mathcal {F}}\) assumed to be non-vertical. To do so, we will denote by \({\mathcal {P}}\) the plane containing the face \({\mathcal {F}}\), and we will label the two endpoints of the segment \({\mathcal {E}}\) as \(A(x_A, y_A, z_A)\) and \(B(x_B, y_B, z_B)\). Finally, we will consider another point \(C(x_C, y_C, z_C)\) in the plane \({\mathcal {P}}\), which does not belong to the line (AB).

By writing \(x_{AB} = x_B-x_A\), \(y_{AB} = y_B-y_A\) and \(z_{AB} = z_B-z_A\), and similarly for \(x_{AC}\), \(y_{AC}\) and \(z_{AC}\), the equation of the plane \({\mathcal {P}}\) containing the points A, B and C can be expressed using the coordinates of points A, B and C as follows:

$$\begin{aligned} z = g^{{\mathcal {F}}}(x,y) = \alpha x + \beta y + \kappa , \end{aligned}$$
(15)

with

$$\begin{aligned} \alpha = - \frac{\Delta _x}{\Delta _z}, \quad \beta = - \frac{\Delta _y}{\Delta _z}, \quad \kappa = \frac{\Delta _x}{\Delta _z} x_A + \frac{\Delta _y}{\Delta _z} y_A + z_A, \end{aligned}$$

and where

$$\begin{aligned} \Delta _x&= y_{AB} \ z_{AC} - y_{AC} \ z_{AB}, \\ \Delta _y&= x_{AC} \ z_{AB} - x_{AB} \ z_{AC}, \\ \Delta _z&= x_{AB} \ y_{AC} - x_{AC} \ y_{AB}. \end{aligned}$$

It should be noted that \(\Delta _z = (\overrightarrow{AB} \times \overrightarrow{AC})_z \ne 0\) because the face \({\mathcal {F}}\) is assumed to be non-vertical. On the other hand, it is easy to verify that the normal vector to the face \({\mathcal {F}}\) can be expressed in terms of \(\alpha \) and \(\beta \) as follows:

$$\begin{aligned} {\hat{{\varvec{n}}}}= \frac{\varepsilon }{N} (\alpha , \beta , -1), \quad \text{ with } \ N=\sqrt{\alpha ^2 + \beta ^2+1}, \end{aligned}$$

where \(\varepsilon =-1\) if the normal vector \( (\alpha , \beta , -1)\) is outgoing from the domain \(D\) and \(\varepsilon =1\) otherwise. Finally, since here the edge \({\mathcal {E}}= [A, B]\) is a line segment assumed to be oriented in the same direction as the closed curve \(\partial {\mathcal {F}}\), a parametrization of \({\mathcal {E}}\) is given by:

$$\begin{aligned} \gamma = \gamma ({\mathcal {E}}, {\mathcal {F}}): {\left\{ \begin{array}{ll} \ [0,1] \longrightarrow {\mathcal {E}}=[A,B] \\ \quad \quad t \longmapsto \begin{pmatrix} x(t) = x_{AB} \ t + x_A \\ y(t) = y_{AB} \ t + y_A \\ z(t) = z_{AB} \ t + z_A \end{pmatrix}. \end{array}\right. } \end{aligned}$$
(16)

So \(y^\prime (t) = y_{AB}\), and finally, the integral (14) can be written as:

$$\begin{aligned} I({\mathcal {E}}, {\mathcal {F}}) = y_{AB} \ \int _0^1 Q^{{\mathcal {F}}}\left( x(t), y(t) \right) \ \textrm{d}t. \end{aligned}$$
(17)

It is worth noting that when the line segment \({\mathcal {E}}= [A,B]\) is perpendicular to the y-axis, we have \(y_{AB} = 0\). Consequently, equation (17) simplifies to \(I({\mathcal {E}}, {\mathcal {F}}) = 0\), which is consistent with Remark 3.

5.2 Case of Polynomial Functions

In this section, we examine the integral given by (17) in the case where the function f(x, y, z) is a polynomial. Since integrating a polynomial amounts to calculating the integral of its monomials, we limit ourselves here to showing how to integrate a monomial \(f(x,y,z) = x^i y^j z^k\) over a polyhedral cell, where i, j and k are non-negative integers. In this case, an antiderivative of f with respect to the z variable can be given by:

$$\begin{aligned} f^\star (x,y,z) = \frac{1}{k+1}x^i y^j z^{k+1}. \end{aligned}$$
(18)

The function \(Q^{{\mathcal {F}}}\), see (9), depends only on x and y and it must satisfy:

$$\begin{aligned} \partial _x Q^{{\mathcal {F}}}(x,y) = f^\star (x,y,g^{{\mathcal {F}}}(x,y)) = \frac{1}{k+1}x^i y^j (\alpha x + \beta y +\kappa )^{k+1}, \end{aligned}$$

using the binomial formula:

$$\begin{aligned} (\alpha x + \beta y +\kappa )^{k+1} = \sum _{\ell =0}^{k+1} \ \left( {\begin{array}{c}k+1\\ \ell \end{array}}\right) \alpha ^\ell x^\ell \ (\beta y +\kappa )^{k+1-\ell }, \end{aligned}$$

it follows that,

$$\begin{aligned} \partial _x Q^{{\mathcal {F}}}(x,y) = \frac{1}{k+1} \ \sum _{\ell =0}^{k+1} \ \left( {\begin{array}{c}k+1\\ \ell \end{array}}\right) \alpha ^\ell x^{\ell +i} \ y^j (\beta y +\kappa )^{k+1-\ell }. \end{aligned}$$

Finally, this allows us to write:

$$\begin{aligned} Q^{{\mathcal {F}}}(x,y) = \frac{1}{k+1} \ \sum _{\ell =0}^{k+1} \ \frac{1}{\ell +i+1} \left( {\begin{array}{c}k+1\\ \ell \end{array}}\right) \alpha ^\ell x^{\ell +i+1} \ y^j (\beta y +\kappa )^{k+1-\ell }. \end{aligned}$$
(19)

Setting \( Q^{{\mathcal {F}}}(t) = Q^{{\mathcal {F}}}(x(t),y(t)) \),

$$\begin{aligned} Q^{{\mathcal {F}}}(t) = \frac{1}{k+1} \ \sum _{\ell =0}^{k+1} \ \frac{1}{\ell +i+1} \left( {\begin{array}{c}k+1\\ \ell \end{array}}\right) \alpha ^\ell x(t)^{\ell +i+1} \ y(t)^j (\beta y(t) +\kappa )^{k+1-\ell }. \end{aligned}$$

By replacing x(t) and y(t) with their expressions given by (16), and after some algebra:

$$\begin{aligned} Q^{{\mathcal {F}}}(t) = \sum _{\ell =0}^{k+1} \ \sum _{m=0}^{\ell +i+1} \ \sum _{n=0}^{j} \ \sum _{p=0}^{k+1-\ell } C(\ell , m, n, p) \ t^{m+n+p}, \end{aligned}$$

with,

$$\begin{aligned} C(\ell , m, n, p) = C^1(\ell , m, n, p) \ C^2(\ell , m, n, p), \end{aligned}$$

where, keeping in mind that binomial coefficients are simple integers, that can be easily computed using Pascal’s triangle,

$$\begin{aligned} C^1(\ell , m, n, p) = \frac{1}{k+1} \frac{1}{\ell +i+1} \left( {\begin{array}{c}k+1\\ \ell \end{array}}\right) \left( {\begin{array}{c}\ell +i+1\\ m\end{array}}\right) \left( {\begin{array}{c}j\\ n\end{array}}\right) \left( {\begin{array}{c}k+1-\ell \\ p\end{array}}\right) , \end{aligned}$$

and

$$\begin{aligned} C^2(\ell , m, n, p) = \alpha ^\ell \beta ^p \ x_{AB}^m x_A^{\ell +i+1-m} \ y_{AB}^{n+p} y_A^{j-n} \ (\beta y_A+\kappa )^{k+1-\ell -p}. \end{aligned}$$
(20)

Finally, denoting by \(q^\star (t)\) an antiderivative of \(Q^{{\mathcal {F}}}(t)\):

$$\begin{aligned} q^\star (t) = \ \sum _{\ell =0}^{k+1} \ \sum _{m=0}^{\ell +i+1} \ \sum _{n=0}^{j} \ \sum _{p=0}^{k+1-\ell } \frac{C(\ell , m, n, p)}{m+n+p+1} t^{m+n+p+1}. \end{aligned}$$

The equation (17) can be written as:

$$\begin{aligned} I({\mathcal {E}}, {\mathcal {F}}) = y_{AB} \ \int _0^1 Q^{{\mathcal {F}}}\left( x(t), y(t) \right) \ \textrm{d}t = y_{AB} \ \left( q^\star (1) - q^\star (0) \right) . \end{aligned}$$

Thus finally,

$$\begin{aligned} I({\mathcal {E}}, {\mathcal {F}}) = y_{AB} \ \sum _{\ell =0}^{k+1} \ \sum _{m=0}^{\ell +i+1} \ \sum _{n=0}^{j} \ \sum _{p=0}^{k+1-\ell } \frac{C(\ell , m, n, p)}{m+n+p+1}. \end{aligned}$$
(21)

In the case where the face \({\mathcal {F}}\) is flat and horizontal, the equation (7), describing the face \({\mathcal {F}}\), simplifies to \(z = g^{{\mathcal {F}}}(x,y) = \kappa \). So, we have \(\alpha = \beta = 0\) in equation (15), and consequently \( \alpha ^\ell \beta ^p = \delta _{\ell ,0}\delta _{p,0}\) in equation (20), where \(\delta \) is the Kronecker symbol. In this scenario, equation (21) simplifies significantly:

$$\begin{aligned} I({\mathcal {E}}, {\mathcal {F}}) = y_{AB} \ \ \sum _{m=0}^{i+1} \ \sum _{n=0}^{j} \frac{C(0, m, n, 0)}{m+n+1}. \end{aligned}$$

6 Line Integral Using the Gradient Theorem

In this section, we present an alternative approach for computing the line integrals \( I({\mathcal {E}}, {\mathcal {F}})\) given by (13), relying on the gradient theorem. We focus exclusively on cases where the edge \({\mathcal {E}}\) is not perpendicular to the y-axis; because otherwise, we have \(I({\mathcal {E}}, {\mathcal {F}}) = 0\) as mentioned in Remark 3. When the curve \({\mathcal {E}}\) is composed of portions that are perpendicular to the y-axis and portions that are not, only the latter contribute to the integral \(I({\mathcal {E}}, {\mathcal {F}})\). In such cases, the calculation must be carried out individually for each of these contributing portions. So, and once again thanks to the implicit function theorem, x can be locally expressed as a function of y along the edge \({\mathcal {E}}\in {\mathcal {F}}\):

$$\begin{aligned} x= e (y), \quad \forall (x,y,z) \in {\mathcal {E}}. \end{aligned}$$
(22)

To provide an explanation for the above equation, let us begin by writing the equation of the orthogonal projection \(P({\mathcal {E}})\) of the space curve \({\mathcal {E}}\) onto the xy-plane as:

$$\begin{aligned} h(x,y) = 0, \quad \forall (x,y) \in P({\mathcal {E}}), \end{aligned}$$
(23)

with function h assumed to be \({\mathcal {C}}^1\). Thus, the edge \({\mathcal {E}}\) belongs to the intersection of the surface \({\mathcal {F}}\) and the vertical surface containing \(P({\mathcal {E}})\). Let \({\hat{{\varvec{n}}}}^\star = ({\hat{{\varvec{n}}}}^\star _x, {\hat{{\varvec{n}}}}^\star _y)\) denote a unit normal vector in the xy-plane to the curve \(P({\mathcal {E}})\). We must have \({\hat{{\varvec{n}}}}^\star _x \ne 0\), because if \({\hat{{\varvec{n}}}}^\star _x = 0\) then \({\hat{{\varvec{n}}}}^\star _y = \pm 1\), which contradicts our assumption that \({\mathcal {E}}\) is not perpendicular to the y-axis. Moreover, a normal vector to the curve \(P({\mathcal {E}})\) is also given by \(\nabla h =(\partial _x h, \partial _y h)\). So \(\partial _x h \ne 0\) because \({\hat{{\varvec{n}}}}^\star _x \ne 0\). Therefore, the implicit function theorem ensures that equation (23) can locally be written in the form (22). In pathological cases where equation (22) holds only piecewise on \({\mathcal {E}}\), the integral over \({\mathcal {E}}\) must be computed separately for each piece.

In application cases, equation (22) is globally valid on the curve \({\mathcal {E}}\). In the case, for instance, where the edge \({\mathcal {E}}\) is a line segment \({\mathcal {E}}= [A, B]\) that is not perpendicular to the y-axis, with endpoints \(A(x_A, y_A, z_A)\) and \(B(x_B, y_B, z_B)\), we have \(y_{AB} \ne 0\) and equation (22) can be expressed as: \(x = e(y) = (x_{AB}/y_{AB})(y - y_A) + x_A\). Since \(P({\mathcal {E}})\) is also a line segment, with its endpoints are given by \((x_A, y_A)\) and \((x_B, y_B)\). In the following, we assume that we have an analytical expression for the function e (22), describing the curve \({\mathcal {E}}\), and that this function is of class \({\mathcal {C}}^1\). Consequently, we can write:

$$\begin{aligned} Q^{{\mathcal {F}}}(x,y) = Q^{{\mathcal {F}}}(e(y),y), \quad \forall (x,y,z) \in {\mathcal {E}}. \end{aligned}$$

And define the function \( \varphi (x,y,z)\), depending only on the variable y, as an antiderivative of \(Q^{{\mathcal {F}}}(e(y),y)\) with respect to the variable y:

$$\begin{aligned} \partial _y \varphi (x,y,z) = Q^{{\mathcal {F}}}(e(y),y). \end{aligned}$$

It should be noted that the functions e and \(\varphi \) depend on the edge \({\mathcal {E}}\) and the face \({\mathcal {F}}\). That is, the functions e and \(\varphi \) should be denoted as \(e^{{\mathcal {E}}, {\mathcal {F}}}\) and \(\varphi ^{{\mathcal {E}}, {\mathcal {F}}}\), but we omit these subscripts to simplify the notation. Moreover, it is easy to verify that:

$$\begin{aligned} {\textbf{G}}^{{\mathcal {F}}}=\nabla \varphi , \quad \forall (x,y,z) \in {\mathcal {E}}. \end{aligned}$$

Finally, the gradient theorem, also said fundamental theorem of calculus for line integrals [9, page 113], implies:

$$\begin{aligned} \int _{{\mathcal {E}}} {\textbf{G}}^{{\mathcal {F}}}\cdot \textrm{d}\textbf{r}= \int _{{\mathcal {E}}} \nabla \varphi \cdot \textrm{d}\textbf{r}= \varphi (B) - \varphi (A), \end{aligned}$$

where A and B are the endpoints of the edge \({\mathcal {E}}\). The above equation reduces the integral of a function over a polyhedron to a straightforward evaluation of the functions \(\varphi \) at the vertices of the polyhedron. Note that if the function to be integrated f, as well as the functions \(g^{{\mathcal {F}}}\) describing the surfaces of the polyhedron and the functions e describing the edges are polynomials, then the functions \(\varphi \) are also polynomials. In this case, the computation of these polynomials \(\varphi \) can be facilitated using a computer program designed to handle polynomials, enabling both the composition of two polynomials and the computation of their primitives.

7 Numerical Experiments

To assess the accuracy of the methods presented in this work, we implemented three methods for calculating the integrals:

Method MP::

based on parameterizing the edges, described in Sect. 5.2,

Method MG::

based on the gradient theorem, described in Sect. 6,

Method ML::

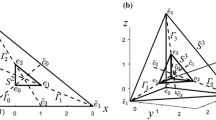
Lasserre’s method, described in [11, 18].

The program is coded in C++, with floating-point numbers represented in double precision. For validation, we consider three polyhedra \(D_a\), \(D_b\) and \(D_c\), whose shapes are illustrated in Fig. 1. The first polyhedron is a simple cube, while the other two are non-convex.

Fig. 1
figure 1

Polyhedra \(D_a\), \(D_b\) and \(D_c\)

Full size image

The coordinates of the vertices of these polyhedra are listed in Table 1.

Table 1 Vertices of polyhedra \(D_a\), \(D_b\) and \(D_c\)
Full size table

The test cases presented here are those studied in [11]. In this article, the authors consider the homogeneous polynomial \(f(x,y,z)= x^2 + xy + y^2 + z^2\) and provide the exact integrals of this polynomial over the three polyhedra \(D_a\), \(D_b\) and \(D_c\). These exact values are recalled in equations (24), (25) and (26):

$$\begin{aligned} I(D_a, f)&= 15625/4 , \end{aligned}$$
(24)
$$\begin{aligned} I(D_b, f)&= 33835/12 , \end{aligned}$$
(25)
$$\begin{aligned} I(D_c, f)&= 37/960, \end{aligned}$$
(26)

where the notation I(D, f) represents the integral of the function f over the polyhedron D. We performed the same calculations using the method outlined in this document for both variants MP and MG. Table 2 presents the results obtained, along with the relative errors in comparison to the exact values provided in equations (24), (25) and (26). Only the first nine significant digits of the results are retained in Table 2.

Table 2 The integrals resulting from the methods MP and MG
Full size table

It is worth noting that the results from the two methods are in excellent agreement with the exact values, within the limits of machine precision. The MG method gives exactly the reference values for the considered integrals.

Table 3 gives the values of the integrals over the polyhedron \(D_c\), for the monomials 1, xyz, \(x^2y^2z^2\), \(x^3y^3z^4\) and \(x^3y^5z^4\), obtained using the MG method, as well as the relative errors of the results from the MP and ML methods compared to MG.

Table 3 The integrals resulting from the methods MP, MG and ML
Full size table

Even though we do not have the exact results of the integrals calculated in table 3, we can observe that the results obtained by the three methods MP, MG, and ML are consistent. This consistency diminishes as the degrees of the monomials increase.

8 Application Cases of the Method

In this paper, we have highlighted the importance of our approach for only the discontinuous Galerkin method (dG), for the simple reason that this work was initiated to extend the numerical scheme based on the (dG) method, proposed in [8] and analyzed in [5], to polyhedral meshes.

However, the method proposed here could also be useful for other methods such as, the virtual element method (VEM) [6, 7] and the Hybrid High Order (HHO) method [13, 15, 16]. The VEM and HHO methods have gained considerable success in recent years, thanks to their capacity to handle polygonal and polyhedral meshes. These methods also require the calculation of polynomial integrals over polyhedra, and the method proposed here can serve as an alternative for such calculations.

In all of these methods, it is preferable, as discussed in [7, 8] and [16, page 451], to assign a local origin \((x_0, y_0, z_0)\) to each element \(D\). This origin can be, for instance, the centroid of the polyhedron’s vertices, and to work with polynomials, cell-based shape functions, whose monomials are written as:

$$\begin{aligned} m^{i,j,k} (x,y,z) = \left( \frac{x-x_0}{h}\right) ^i \left( \frac{y-y_0}{h}\right) ^j \left( \frac{z-z_0}{h}\right) ^k, \end{aligned}$$

where h is the diameter of the element D, the functions \(m^{i,j,k} (x,y,z)\) are called scaled monomials, see [7] for an explanation of this terminology. The calculation of elementary matrices, such as the mass or stiffness matrix, involves integrals of scaled monomial products, either directly or indirectly, which are written as:

$$\begin{aligned} \int _Dm^{i,j,k} (x,y,z) \ m^{i^\prime ,j^\prime ,k^\prime } (x,y,z) \ \textrm{d}x \textrm{d}y \textrm{d}z. \end{aligned}$$
(27)

In the VEM method, the integrals (27) do not directly appear in the stiffness matrix but in an auxiliary matrix, see [7].

And since the product of two scaled monomials is a scaled monomial of the same form, this leads to integrals of the form:

$$\begin{aligned} \int _D\left( \frac{x-x_0}{h}\right) ^i \left( \frac{y-y_0}{h}\right) ^j \left( \frac{z-z_0}{h}\right) ^k \textrm{d}x \textrm{d}y \textrm{d}z. \end{aligned}$$

The advantage of working with scaled monomials is that the above integrals are equal for two equivalent elements, i.e., identical up to a translation, which can be easily verified by a trivial change of variables. This can significantly reduce the computation of these integrals when the mesh contains many elements that are identical up to a translation. Section 5.2 can be easily adapted for the integration of scaled monomials.

Scaled monomials are not homogeneous functions, and the method provided in [11] does not directly apply to scaled monomials. The method in [11] requires first expanding the scaled monomials and integrating each non-scaled monomial.

Finally, let’s say a word about the finite volume method. This method only requires the calculation of cell volumes. The method presented here also enables the calculation of volumes. Specifically, the volume of the domain \(D\) can be represented as an integral in the form of equation (2) with \(f(x,y,z)=1\), which reduces equation (4) to \(f^\star (x,y,z)=z\). Consequently, the vector fields \({\textbf{F}}\) and \({\textbf{G}}^{{\mathcal {F}}}\) are simplified as \({\textbf{F}}(x,y,z)= (0,0, z)\) and \({\textbf{G}}^{{\mathcal {F}}}(x,y,z)=(0,g^{{\mathcal {F}},\star }(x,y),0)\), where \(g^{{\mathcal {F}},\star }(x,y) = Q^{{\mathcal {F}}}(x,y)\) serves as an antiderivative of \(g^{{\mathcal {F}}}(x,y)\) with respect to x variable. Finally, equation (21) is simplified in this case by setting \(i=j=k=0\).

9 Conclusion and Comments

In this document, we presented a method for integrating smooth functions over arbitrary polyhedra. This volume integral is reduced to line integrals along the edges of the polyhedron, see equation (12). In general, these line integrals can be approximated using quadrature formulas. However, for classical polyhedra with flat faces and straight edges, and when the function to be integrated is a polynomial, the calculations can be carried out exactly. We have provided the analytical formula for these line integrals in such cases. The proposed approach also allows for the calculation of integrals over polyhedra with curved surfaces, and in an exact manner in some situations. This is the case, for example, when the surfaces of the polyhedron are described using polynomials, as mentioned in Sect. 6.

Two approaches for computing the line integrals have been proposed: the first involves parameterizing the edges, while the second relies on the gradient theorem. Implementing both methods allows for cross-validation of the computed integrals.

The discontinuous finite element method introduces, in addition to volume integrals, surface integrals of vector fields over the interfaces of elements. These integrals are written in the form (6). The computation of these integrals has also been done in this document.

In the approach used in this document, we employed a vertical vector field \({\textbf{F}}\) with only its z-axis component is non-zero, showing that this choice allowed us to eliminate the vertical faces in the volume integral. Other choices are also possible: the vector field \({\textbf{F}}\) can be chosen to align with either the x-axis or the y-axis. Selecting a field along the x-axis eliminates faces parallel to this axis in the volume integral, and similarly, choosing a field along the y-axis removes contributions from faces parallel to the y-axis. This flexibility allows the method to be tailored based on the number of faces parallel to each of the x, y, and z axes.