1 Introduction

Managing large, multi-vendor networks with diverse technologies is becoming more expensive due to resource shortages and increasing real estate costs for service providers [1]. A new network paradigm is needed to integrate network provisioning and management across multiple domains [2].

Software defined network (SDN) offers a solution by separating the control plane from the data plane in network devices such as switches and routers [3, 4]. Traditionally, these two planes are closely connected in conventional networks, which can make managing and scaling the network more difficult [5, 6]. SDN architecture uses a central controller to manage the network [7], communicating with switches and routers via a standard protocol such as OpenFlow. OpenFlow, developed through a collaboration between Stanford University and the University of California, Berkeley, has become a widely used protocol in SDN. It was later standardized by the Open Networking Foundation (ONF) to ensure consistency and interoperability within SDN environments [8]. One of the key benefits of SDN is that it makes networks more scalable and flexible, allowing for the creation of virtual networks customized for specific applications or types of traffic [9].

Adding intelligence to networking devices is essential for simplifying optimization, organization, maintenance, and management. However, the distributed nature of networking systems complicates the inclusion of artificial intelligence (AI) for device control [10]. A key advantage of SDN is its ability to support network programmability, making integrating AI into communication networks easy [11].

Machine learning (ML) plays a critical role in facilitating AI [12] by proficiently predicting and scheduling network resources using available data inputs [13, 14]. It strives to empower computers to improve their performance autonomously over time, without the need for explicit programming [15]. ML algorithms encompass supervised, unsupervised, semi-supervised, or reinforcement learning (SL, USL, SSL, or RL respectively) approaches, which vary based on the type of data employed for model training [16, 17].

SL involves training the model with labeled data, where the correct output is known for each input. USL entails identifying patterns and relationships within unlabeled data. SSL combines elements of both SL and USL [18]. In RL, an agent learns to interact with its environment in such a way that it maximizes the rewards received [19]. Ensemble learning (EL) methods combine the strengths of several models to improve prediction accuracy and decision-making [20]. By integrating ML into SDN, network managers can create networks that are more efficient, flexible, and safe. In our paper, we focus on SL and EL ML models.

In SDN, many tasks can benefit from leveraging ML algorithms, such as traffic classification (TC) [21, 22]. Many applications now require strict QoS to meet their demands [23]. ML can classify network traffic based on the type of application or user behavior, enabling the prioritization of high-priority traffic and ensuring that critical applications receive the necessary Quality of Service (QoS) levels. This improves customer satisfaction and experience, particularly for applications requiring real-time responses, low latency, or high throughput [24].

1.1 Motivation

1.1.1 Supervised and Ensemble Learning Models in SDN

Authors in Ref. [25] explore the integration of SDN and ML for effective network TC. The study employed supervised ML models (e.g., Decision Tree (DT), and Random Forest (RF)), an ensemble model (AdaBoost), and unsupervised K-means clustering on traffic types such as DNS, Telnet, Ping, and Voice. Using Mininet for SDN simulation and the Distributed Internet Traffic Generator (D-ITG) for dataset creation, the DT model achieved the highest classification accuracy (99.81%), and the AdaBoost ensemble method achieved 99.7%.

Three ensemble-based network traffic classification algorithms (XGBoost, GBM, and LightGBM) along with SL algorithms like DT and RF, were evaluated on a real-world network traffic dataset (ISCX dataset) in Ref. [26]. The dataset was used for training and testing, with traffic classified into different classes according to QoS requirements. The results showed accuracy, ranging from 92.64 to 96.15%.

Ref. [27] has demonstrated that ensemble algorithms can serve as effective preprocessing tools for SDN, enabling robust and reliable classification across various traffic types. Performance tests were performed using traffic trace data collected with WireShark for five types of application, each representing a distinct type of traffic. The study used the XGBoost algorithm, a well-known boosted tree learning model, to predict the final results, achieving a performance of up to 99. 2%.

Another effort proposed a model that integrates ML algorithms into SDN for TC [10]. This study utilized SL algorithms, including SVM, NB, and Nearest Centroid, using a custom dataset. The results demonstrated that these SL models achieved an accuracy of over The accuracy obtained for SVM is 92.3, 96.79, and 91.02% respectively.

A study focused on classifying traffic in SDNs in an application-aware manner using SL and ensemble methods, including RF, stochastic gradient boost (SGB), and XGBoost [28]. The researchers utilized a labeled dataset generated from their custom network topology and developed an SDN application specifically designed to collect OpenFlow statistics from controlled switches. The experimental results demonstrated varying levels of accuracy for the models: RF achieved an accuracy range of 73.6% to 96.0%, SGBoost achieved 71.2% to 93.6%, and XGBoost achieved 73.6 to 95.2%. These findings highlight the potential of ensemble learning methods in improving traffic classification performance in SDNs.

To sum up the gaps, feature scaling plays a crucial role in enhancing the accuracy and efficiency of ML models. Although some studies incorporate feature scaling in their methodologies, they often limit their analysis to a single technique. This approach overlooks the fact that different scaling techniques can influence the performance of ML models. The evaluation of multiple scaling methods is essential to determine the most effective approach for each model, ensuring optimal classification accuracy and improved performance.

1.1.2 Reinforcement Learning in SDN

The massive volume of data generated by modern applications and services often leads to network congestion, negatively impacting QoS and the overall user experience. To address this issue, the authors in Ref. [29] propose a novel congestion control approach in SDN using a Multi-Agent RL (MARL) framework. Their study evaluates the convergence of two popular RL algorithms, Q-learning and SARSA, to determine the most suitable algorithm for their proposed system. Experimental results demonstrate that Q-learning outperforms SARSA, making it the optimal learning algorithm for managing network congestion effectively.

To improve traffic management in a multi-layer hierarchical SDN [30], introduced the use of the SARSA algorithm for QoS provisioning. When a new flow arrives, the switch communicates with the SDN controller. The controller uses the SARSA algorithm to identify the QoS requirements of the flow and calculate the best traffic path to meet those requirements. Each step in the path is determined by the next hop in the switch, ensuring the flow moves efficiently from the source to the destination.

However, we plan to compare our results with studies closely aligned with our research focus, aiming to achieve and demonstrate outstanding performance.

1.1.3 Hybrid Machine Learning in SDN

In Ref. [31], the authors explored the detection and classification of conflicting flows in SDNs using various ML algorithms, such as decision tree (DT), SVM, extremely fast decision tree (EFDT), and a hybrid DT-SVM model. The EFDT and hybrid DT-SVM algorithms were specifically developed to improve performance by combining features of DT and SVM. The experiments were carried out on two different network topologies, a simple tree, and a fat tree, with flow volumes ranging from 1,000 to 100,000. The findings showed that the EFDT algorithm achieved the highest accuracy.

However, the paper does not address QoS in SDNs, leaving a gap in understanding how the hybrid model performs in scenarios requiring QoS management and optimization.

1.2 Contribution

The paper’s contributions include the following:

  • Applying a wider variety of ML models, including DT, SVM, KNN, XGBoost, and Hybrid models (e.g., DT-SVM, KNN-SVM).

  • Evaluating the performance of these models using multiple metrics to provide a comprehensive analysis and showing that the models’ performance is consistent across various train-test split ratios.

  • Implementing different feature scaling methods and pointing to the one that achieves the highest accuracy for each model.

  • Analyzing the impact of feature scaling on the performance of the designated ML models.

  • Investigating the computational efficiency of each model, highlighting the trade-offs between accuracy and execution time.

The paper is organized as follows: Sect. 2 provides the methodology. ML models used for TC are discussed in Sect. 3, while Sect. 4 presents the used evaluation metrics. Results and discussion are introduced in Sect. 5. Finally, Sect. 6 covers the conclusion and future work.

2 Methodology

This section describes the approach used to address the research problem in which the IEEE DataPort dataset is used. We preprocessed the data to address class imbalance and evaluate ML models under various scenarios.

2.1 Dataset

The dataset used in this study was obtained from IEEE DataPort [32]. The dataset is exclusively derived from OpenFlow switch statistics and processed by an SDN application. It includes 37 features, each record capturing information periodically collected from flows within an OpenFlow switch. In total, the dataset contains 662,828 records, consisting of 221,564 normal records and 441,264 attack records. The parameters are grouped as follows:

  • Flow Identifier Features: Include parameters like flow-id, EtherType (eth-type), source ipv4 address (ipv4-src), destination ipv4 address (ipv4-dst), IP protocol (ip-proto), source port number (src-port), destination port number (dst-port), and flow-duration for flow identification (flow-duration).

  • Packet-Based Features: Cover statistics such as total packets per flow, packets per time unit, and sample periods.

  • Byte-Based Features: Provide information on total bytes per flow, bytes per flow per time unit, and sample periods.

  • Flow-Timer Features: Track uptime and downtime for each flow.

  • Cumulative Features: Aggregate metrics like total packets/bytes per source and destination IP, and total connections per source and destination IP, offering an overview of network activity.

2.2 Dataset Preprocessing

In our study, we focus on the normal records dataset, excluding the attack records. The dataset’s Category feature consists of 7 applications: Streaming, HTTP, DNS, FTP, SSH, ICMP, and NTP. The number of records for each application varies significantly, which can negatively impact the performance of ML models by creating biased models that favor the majority classes, thus reducing overall accuracy and reliability.

To address this issue, we balanced the dataset by removing records from over-represented categories to ensure an equal number of records for each application. Our approach is evaluated across four scenarios:

  • Scenario 1: Multi-class classification using the above mentioned seven application labels without scaling the features.

  • Scenario 2: Multi-class classification using the above mentioned seven application labels with scaling the features.

  • Scenario 3: Binary classification with two labels without scaling the features.

  • Scenario 4: Binary classification with two labels with scaling the features.

For Scenarios 1 and 2, each application was then assigned a numerical label from 0 to 6, serving as the target variable for our classification models. In Scenarios 3 and 4, we assigned two labels: streaming (label "0") and all other applications (label "1"), to evaluate how our models can prioritize streaming traffic, which is an important factor in ensuring QoS.

In the binary classification scenarios (Scenarios 3 and 4), we encountered an imbalance where streaming records were significantly fewer than the combined records of other applications. To balance the data, we applied an augmentation algorithm, the synthetic minority over-sampling technique (SMOTE) [33, 34], generating additional synthetic streaming records to create a more balanced dataset.

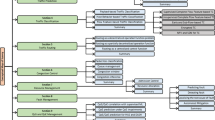
It is worth mentioning that scaling techniques play a crucial role in optimizing the performance of ML models, so it is used in scenarios 2 and 4. In this analysis, we compare the effectiveness of different scaling methods-standard scaling, min-max scaling, maxabs scaling, and robust scaling-on various ML models, including SVM, DT, KNN, XGBoost, Hybrid DT-SVM, and Hybrid SVM-KNN. The results are presented in two tables, one for multi-class classification and the other for binary classification. Figure 1 summarizes the workflow of the proposed approach including the dataset preprocessing.

Fig. 1
figure 1

Overview of the data preprocessing and classification process used in the SDNFLOW dataset study

Full size image

2.3 Integration of ML Model in SDN Architecture

As shown in Fig. 2, the ML model would be integrated into the SDN control plane. The control plane is responsible for making decisions about how traffic should be handled across the network, which includes TC and QoS optimization. When a packet arrives at a switch in the data plane, it is initially checked for an existing flow entry. If no matching rule is found, the packet is sent to the control plane using a Packet-In message. The SDN controller then processes the packet and uses the ML model to classify the traffic, determining its type and specific QoS requirements. Based on the classification results, the controller calculates the necessary QoS policies and sends the information back to the switch in the form of a Flow-Mod message. The switch then updates its flow table with the new rules, enabling it to forward the packet according to the newly defined QoS policies.

Fig. 2
figure 2

Integration of machine learning models in SDN architecture

Full size image

3 ML Models Used for Traffic Classification

ML for TC is a powerful technique that enables computers to automatically learn patterns and make decisions based on labeled data. By applying algorithms and statistical models, ML classifiers categorize input data into predefined classes or labels. This process involves training the model on a labeled dataset to learn how input features relate to target labels. Once trained, the classifier can generalize to new, unseen data, accurately predicting the class labels of future inputs.

To implement the proposed solution in an SDN environment, the process is straightforward as it mainly involves calling predefined functions. The SDN controller, such as Ryu or OpenDaylight, manages traffic by collecting flow statistics from OpenFlow-enabled switches, which are then used as features for TC model. The XGBoost model (highest accuracy), is integrated for real-time classification with minimal configuration, prioritizing latency-sensitive traffic and adjusting resources for less critical traffic. Tools like Mininet can be easily installed with just a few commands and are commonly used to simulate SDN networks without complex setup. Additionally, Wireshark can be used to monitor and validate performance, with little configuration required.

Here, we outline a classification of the prevalent linear and nonlinear ML models utilized in our framework.

3.1 Linear Classification Models

3.1.1 Support Vector Machine (SVM) with Linear Kernel

Linear SVMs are a subtype of SVMs that are specifically designed for linearly separable data or data that can be transformed into a linearly separable form in the feature space. These models aim to find a hyperplane that best separates the classes in the input data with the maximum margin, which is the distance between the hyperplane and the closest data points (support vectors) from each class [35, 36].

3.2 Non-Linear Classification Models

3.2.1 Decision Tree (DT)

This method is displayed as a tree structure, where the features of the dataset are represented by internal nodes, and the branches correspond to the decision criteria, with outcomes expressed by leaf nodes [31]. This approach determines information gains by calculating entropy on the dataset, which is then used to classify the data. The entropy H of a dataset is defined as:

$$\begin{aligned} H(D) = - \sum _{k=1}^{n} p_{k} \log _2 p_k, \end{aligned}$$
(1)

where \(p_k\) is the proportion of instances belonging to class k in the dataset D. Using this entropy calculation, the algorithm identifies the root node based on the highest information gain. This process is repeated to split branches and complete the tree [37].

DTs have several advantages, such as being easy to interpret and visualize, automatically performing feature selection, and effectively handling non-linear relationships between parameters. One major benefit of DTs is that they do not require feature scaling. This is because DTs work by splitting data based on feature thresholds, rather than relying on distance calculations or gradients. This characteristic makes DTs especially robust when working with datasets that include features with different scales or units. As a result, DTs are a straightforward yet powerful tool for both classification and regression tasks, making them a popular choice in various machine learning applications.

3.2.2 K-Nearest Neighbors (KNN)

KNN is another supervised learning technique that classifies an unclassified sample by looking at the classes of its k nearest neighbors [38]. The KNN algorithm is based on a simple idea: If most of a sample’s K nearest neighbors belong to a particular class, the sample is classified as part of that class [39]. The algorithm follows these steps:

  1. 1.

    Select the value of K, which indicates the number of neighbors to consider.

  2. 2.

    Compute the Euclidean distance for each of the K neighbors.

  3. 3.

    Identify the K nearest neighbors based on these distances.

  4. 4.

    Count how many data points from each class are among the K neighbors.

  5. 5.

    Assign the new data point to the class that appears most frequently among the K neighbors.

KNN is easy to implement, achieves high accuracy, computes features efficiently, and is suitable for multiclass classification. However, KNN can be time-consuming when dealing with large datasets [40].

Feature scaling significantly impacts the performance of KNN. Since it relies on distance calculations to identify the nearest neighbors, features with larger scales can disproportionately influence the distance metric, leading to biased classifications [41].

3.2.3 Extreme Gradient Boosting (XGBoost)

XGBoost, short for "Extreme Gradient Boosting," is a ML algorithm that implements the gradient boosting framework [42]. It is designed to be efficient and flexible [43]. Gradient boosting is an ensemble ML technique aimed at enhancing the effectiveness of weak learners, such as classifiers or regressors, transforming them into robust learners [44]. The method operates by iteratively training multiple models, with each subsequent model concentrating on the examples that previous models misclassified. This sequential approach assigns greater importance to misclassified instances, enabling subsequent models to focus more on correcting these errors. As a result, individual predictors become specialized in different segments of the dataset, leading to a reduction in both bias and variance [45].

3.3 The Proposed Hybrid Classification Models

3.3.1 SVM-DT

The Hybrid SVM-DT model combines the strengths of both SVMs and DTs to improve classification performance. This hybrid approach aims to utilize SVM’s ability to optimize the margin between classes and DT’s efficiency in decision-making, providing a balanced and effective classification method.

3.3.2 KNN-SVM

The Hybrid SVM-KNN model merges the capabilities of SVM and KNN to create a robust and flexible classifier. SVM performs exceptionally well at finding the optimal hyperplane that separates different classes, which is especially useful in high-dimensional datasets. Meanwhile, KNN is a straightforward algorithm that classifies data points based on the majority class among their closest neighbors. By combining these methods, the Hybrid SVM-KNN model can benefit from SVM’s margin optimization and KNN’s local, instance-based learning approach, resulting in a powerful tool for classification tasks.

4 Evaluation Metrics

This section outlines the metrics used to evaluate the performance of ML models. These will help measure the effectiveness and reliability of the developed approaches in different scenarios.

4.1 Accuracy

Accuracy is a widely used metric for evaluating classification models. It shows how often the model’s predictions match the actual outcomes. Specifically, accuracy is calculated by dividing the number of correct predictions by the total number of predictions. The formula for accuracy is given by:

$$\begin{aligned} Accuracy = \frac{P_C}{P_T}, \end{aligned}$$
(2)

where \(P_C\) represents the count of correct predictions and \(P_T\) is the total count of predictions. Accuracy works well when the classes in the dataset are balanced, meaning each class has roughly the same number of instances. However, it can be misleading with imbalanced datasets, where one class is much more common than others. For example, in a dataset where one class dominates, a model that always predicts the majority class will have high accuracy, even though it might not perform well on the minority class [46].

Despite this, accuracy remains a popular metric for evaluating overall model performance. To get a clearer picture, it is often used with other metrics like precision, recall, and F1 score.

4.2 F1-Score

The F1 score is a metric that helps in the evaluation of a classification model by balancing both precision and recall [47]. It is especially useful when dealing with imbalanced classes, where some classes are much more common than others. Unlike accuracy, which might give a false sense of how well the model is performing when classes are imbalanced. By considering both precision and recall, the F1 score provides a clearer picture of a model’s performance in challenging scenarios. The F1 score is defined by the formula:

$$\begin{aligned} F1score=2 \times \frac{Pr \times R}{Pr+R}, \end{aligned}$$
(3)

where Pr is the precision and R is the recall. The F1 Score ranges from 0 to 1, where 1 represents perfect precision and recall, and 0 indicates the poorest performance.

4.3 Kappa Score

The Kappa score, or Cohen’s Kappa, is a metric that evaluates how well a classification model performs by accounting for the accuracy that might occur just by chance. The formula for Cohen’s Kappa is:

$$\begin{aligned} \kappa = \frac{A_o - A_e}{1 - A_e}, \end{aligned}$$
(4)

where \(A_o\) is the observed accuracy and \(A_e\) is the expected accuracy. The Kappa score ranges from −1 to 1. A score of 1 means perfect agreement between the model’s predictions and the actual outcomes. A score of 0 means the model’s performance is as effective as random chance. Negative values indicate that the model performs worse than what you’d expect by random guessing.

4.4 ROC Curve

The Receiver Operating Characteristic (ROC) curve is a tool for evaluating the performance of classification models. It graphs the true positive rate (TPR) against the false positive rate (FPR) across different thresholds. The TPR, also called sensitivity or recall, measures how well the model correctly identifies positive instances. On the other hand, the FPR shows the ratio of false positives (incorrectly predicted positives) to all actual negative instances.. It is calculated as:

$$\begin{aligned} FPR=\frac{FP}{FP+TN}. \end{aligned}$$
(5)

The ROC curve is created by varying the decision threshold of the classifier. Each point on the ROC curve represents a TPR and FPR pair corresponding to a specific threshold.

The AUC of ROC curve is a single scalar value that summarizes the overall performance of a classifier. A perfect model has an AUC of one. A model with a high TPR and low FPR will have a curve that bows towards the top-left corner of the plot.

4.5 Confusion Matrix

A confusion matrix is a tool used to assess the performance of the classification model by providing a detailed breakdown of correct and incorrect predictions. The matrix compares the actual target values with the values predicted by the model. The confusion matrix is extended to an \(K \times K\) matrix, where K is the number of classes. Each cell in the matrix represents the count of instances for a true class (row) and a predicted class (column). Moreover, the confusion matrix enables the calculation of various evaluation metrics such as precision, recall, and F1 score.

5 Results and Discussion

Our experiment results are shared in this section. We analyze how each model performs under different conditions in the designated SDN environment. Different evaluation metrics are used to assess their effectiveness and stability, and we discuss what these results mean in real world terms, as well as highlight each model’s strengths and weaknesses.

The modeling of the proposed solution was conducted using Anaconda Jupyter Notebook as the development environment, with key Python libraries including Pandas for data manipulation, Scikit-learn for machine learning model training and evaluation, Matplotlib for visualizing results such as ROC curves, and Seaborn for enhanced visualization of the confusion matrix. The experiments were performed on a laptop with an AMD Ryzen 7 7730U processor (2.00 GHz), 16 GB RAM, and a 64-bit Windows operating system.

5.1 Evaluation of Different Train-Test Split Ratios

We examined four different train-test split ratios of the utilized SDN dataset as shown in Tables 1 and 2 to evaluate the performance of our models. Since the results are consistent across different test values, we will present only the results for test = 30% in our paper. The test split ratio of 30% is chosen for presentation because it provides a balanced representation of model performance while maintaining consistency across various test ratios. Our analysis shows that the results are stable and similar across different test ratios, indicating that a 30% test split is sufficiently representative of the models’ general performance. This allows us to clearly illustrate the evaluation metrics without redundancy.

Table 1 Accuracy percentage of different test values in multi-class classification scenario before scaling
Full size table
Table 2 Accuracy percentage of different test values in multi-class classification scenario after scaling
Full size table

5.2 Impact of Scaling Techniques on Model Performance

The comparison of model performance with various scaling techniques for multi-class and binary-class classification as presented in Tables 3 and 4 reveals notable differences. In the multi-class classification, SVM shows substantial improvement with min-max and maxabs scaling, achieving almost perfect performance, while with robust scaling it drops significantly to 30.49%. DT and XGBoost maintain consistently high accuracy across all scaling methods, with slight variations. KNN and Hybrid SVM-KNN models also benefit markedly from min-max and maxabs scaling, with a noticeable performance drop when robust scaling is applied. In binary classification, SVM again shows excellent performance with min-max and maxabs scaling, achieving 99.97%, but its performance deteriorates with robust scaling. DT and XGBoost exhibit uniformly high performance across all scaling techniques. KNN and Hybrid SVM-KNN models perform exceptionally well with min-max and maxabs scaling and retain high accuracy with robust scaling. Overall, min-max and maxabs scaling emerge as the most effective techniques for enhancing model performance, particularly for SVM, KNN, and hybrid models; where the accuracy ranges from 99.53% to 99.97%. These findings underscore the importance of selecting appropriate scaling techniques to optimize model performance, with min-max and maxabs scaling being the most reliable choices across different models and classification tasks.

Table 3 Comparison of model performance (accuracy percentage) using various scaling techniques for multi-class classification
Full size table
Table 4 Comparison of model performance (accuracy percentage) using various scaling techniques for binary classification
Full size table

For each model, we used the optimal scaling method identified in our initial analysis to evaluate our scenarios. The scenarios are evaluated using five key metrics: accuracy, F1 score, Kappa score, ROC curve, and confusion matrix. These metrics provide a comprehensive understanding of the models’ performance from various perspectives.

5.3 Models Performance Using Accuracy, F1-Score, and Kappa Score

We will start by discussing scenarios 1 and 3, which are without scaling. Then, scenarios 2 and 4 after data scaling will be illustrated to emphasize the ML models accuracy improvement after scaling.

For scenario 1: the DT model as shown in Figs. 3 and 4 demonstrates high accuracy (99.81%), F1 score (99.80%), and Kappa score (99.75%), indicating that it effectively captures the structure of the dataset. The high performance of DT can be attributed to its ability to handle complex decision boundaries and its robustness to overfitting with proper pruning. The execution time is also low (3.35 s), making DT a practical choice for efficient and accurate classification.

Fig. 3
figure 3

Performance comparison of ML models for multi-class classification before scaling

Full size image
Fig. 4
figure 4

Execution time comparison of ML models for multi-class classification before scaling

Full size image

In contrast, the SVM model performed poorly with low accuracy (41.67%), F1 score (38.18%), and Kappa score (19.49%), underscoring its reliance on feature scaling for optimal performance. Its high execution time (97.62 s) further highlights the computational challenges of using SVM on unscaled data, emphasizing the importance of preprocessing steps like normalization.

KNN achieved moderate performance with an accuracy of 61.22%, F1-score 61.22%, and Kappa score 48.49%. These results reflect its sensitivity to unscaled features, which affect distance-based computations. Despite this, KNN took the least time to run (1.66 s) making it computationally efficient.

XGBoost emerged as one of the best-performing models, with accuracy (99.95%), F1 score (99.95%), and Kappa score (99.94%). Its success is due to the boosting approach, which combines weak learners into a strong classifier. Furthermore, its low execution time (2.81 s) makes it well-suited for high-performance applications.

The hybrid SVM-DT model achieved metrics comparable to the standalone DT model, with accuracy (99.81%), F1 score (99.81%), and Kappa score (99.75%), reflecting the dominant influence of the DT component. However, its high execution time (96.66 s) points to the computational cost introduced by the SVM component. This model demonstrates both the advantages of hybrid approaches in maintaining high accuracy and their disadvantages in terms of computations.

The results indicate that the hybrid KNN-SVM approach has almost the same level of accuracy as the standalone KNN method with moderate accuracy, F1 score, and Kappa score (60.75%, 61.76%, and 47.56% respectively). This similarity suggests that KNN’s characteristics dominate the hybrid model’s performance. The high execution time (95.89 s) reflects the added complexity of combining the two methods.

For scenario 3: as observed in Figs. 5 and 6, DT demonstrated near-perfect performance, with accuracy (99.97%), F1 score (99.97%), and Kappa score (99.94%). Its low execution time (1.8 s) further reinforces its efficiency.

Fig. 5
figure 5

Performance comparison of ML models for binary classification before scaling

Full size image
Fig. 6
figure 6

Execution time comparison of ML models for binary classification before scaling

Full size image

SVM underperformed in comparison to DT, with lower accuracy (79.05%), F1 score (78.21%), and Kappa score (57.87%). Its high execution time (146.61 s) limits its practicality without further optimization.

KNN achieved high accuracy (94.96%), F1 score (94.96%), and Kappa score (89.92%) though slightly lower than DT. Despite this, its execution time is moderate (4.07 s), balancing between computational efficiency and performance.

XGBoost matched DT’s performance metrics and maintained a low execution time (3.11 s), showcasing its robustness and efficiency.

The hybrid SVM-DT model matched the individual DT model’s performance but exhibited a higher execution time (135.55 s), while the hybrid KNN-SVM model showed slightly improved metrics over standalone KNN (96%, 96%, and 92%, respectively), with a significant increase in execution time (139.27 s).

For scenario 2: as presented in Figs. 7 and 8, post-scaling, SVM shows a marked improvement in accuracy, F1 score, and Kappa score (99.91, 99.89, and 99.88% respectively). Despite a reduced execution time (19.63 s), it remains computationally intensive.

Fig. 7
figure 7

Performance comparison of ML models for multi-class classification after scaling

Full size image
Fig. 8
figure 8

Execution time comparison of ML models for multi-class classification after scaling

Full size image

DT maintained its high metrics: accuracy (99.81%), F1 score (99.81%), and Kappa score (99.75%). Its ability to handle scaled data efficiently is supported by its low execution time (1.6 s).

The KNN model also benefitted from scaling, with accuracy (99.53%), F1 score (99.51%), and Kappa score (99.58%). Feature normalization enhanced its performance while retaining a low execution time (3.34 s).

XGBoost continued its strong performance with accuracy (99.95%), F1 score (99.95%), and Kappa score (99.94%). Its execution time (2.21 s) remained low, reinforcing its suitability for computationally efficient, high-performance tasks.

The hybrid SVM-DT model achieved comparable metrics to DT alone but with a higher execution time (18.68 s), reflecting the SVM component’s complexity. Similarly, the hybrid KNN-SVM model improved post-scaling, with accuracy (99.76%), F1 score (99.76%), and Kappa score (99.69%). However, its high execution time (21.4 s) highlights the computational trade-offs of hybrid approaches.

For scenario 4: as shown in Figs. 9 and 10, DT, SVM, and XGBoost demonstrated near-identical performance metrics (99.97, 99.97, and 99.94% for accuracy, F1 score, and Kappa score, respectively). However, SVM had the longest execution time, highlighting its computational cost despite its strong classification ability post-scaling.

Fig. 9
figure 9

Performance comparison of ML models for binary classification after scaling

Full size image
Fig. 10
figure 10

Execution time comparison of ML models for binary classification after scaling

Full size image

KNN performed slightly lower, with accuracy (99.73%), F1 score (99.73%), and Kappa score (99.46%). Its moderate execution time (3.98 s) balances performance and efficiency.

The hybrid SVM-DT and KNN-SVM models maintained similar accuracy levels to their standalone components but at the cost of significantly higher execution times (13.58 s and 21.4 s, respectively).

5.4 Models Performance Using ROC Curve Results and Confusion Matrix

For scenarios 1 and 2: the final results obtained by ROC curves are mentioned in Tables 5 and 6, showing significant improvements after scaling the features. Before scaling, DT, XGBoost, and SVM-DT models achieved near-perfect classification (AUC = 1) for all classes except Class 5, which had an AUC of 0.85. SVM showed inconsistent performance across classes, with AUCs ranging from 0.44 to 0.84, while KNN performed well overall, though with lower AUCs for Class 3 (0.74) and Class 5 (0.93). The hybrid KNN-SVM model displayed robust performance, with slightly reduced performance for Class 6 (AUC = 0.88).

Table 5 ROC curve AUC values for multi-class classification before scaling
Full size table
Table 6 ROC curve AUC values for multi-class classification after scaling
Full size table

After scaling, all models achieved perfect classification (AUC = 1) across all classes. This demonstrates the significant positive impact of feature scaling, particularly for SVM and KNN, which rely on distance-based calculations. The reduced performance observed for Class 5 before scaling highlights sensitivity to class imbalances, as this class had significantly fewer labels than others.

For the binary classification scenarios (scenarios 3 and 4) shown in Tables 7 and 8, DT, XGBoost, and hybrid SVM-DT models achieved an AUC of 1 for both labels before scaling, indicating perfect performance. SVM showed moderate performance with an AUC of 0.86 for both labels, while KNN exhibited high performance with an AUC of 0.99. both achieved perfect classification (AUC = 1) for both labels, and hybrid KNN-SVM displayed high performance with an AUC of 0.99.

Table 7 ROC curve AUC values for binary classification before scaling
Full size table
Table 8 ROC curve AUC values for binary classification after scaling
Full size table

After scaling, all models demonstrated perfect classification (AUC = 1) for both classes. This indicates that feature scaling positively impacts binary classification performance, particularly for SVM and KNN.

As shown in Fig. 11, the confusion matrices illustrate the performance of the best models for different scenarios. In Fig. 11a, the XGBoost model demonstrates excellent performance in the first and second scenarios, with nearly no misclassifications across the 7-label dataset. This indicates that XGBoost is well-suited for handling the complexity of multi-class data, effectively balancing between precision and recall for all classes.

Fig. 11
figure 11

Confusion matrix of the Best models in each scenario. a Best model performance in multi-class classification scenarios which is XGBoost, and b Best models for binary classification before scaling (XGBoost, DT, Hybrid DT-SVM) and after scaling (XGBoost, DT, SVM, Hybrid DT-SVM, Hybrid KNN-SVM)

Full size image

In Fig. 11b, the models employed in the third scenario (XGBoost, DT, and hybrid DT-SVM) and in the fourth scenario (XGBoost, DT, SVM, hybrid DT-SVM, and hybrid KNN-SVM) exhibit strong performance. While near-perfect classification is observed in many cases, slight variations in performance across models suggest that some algorithms may be more sensitive to specific characteristics of the dataset, such as label distribution or feature scaling.

5.5 Summary of Key Findings

The following points summarize the performance of the four scenarios with and without feature scaling, evaluated using accuracy, F1-score, Kappa score, ROC curve values, and confusion matrices:

  • Feature scaling had a significant positive impact on model performance, particularly for SVM and KNN, highlighting the importance of appropriate preprocessing in improving classification outcomes.

  • DT and XGBoost consistently delivered high accuracy and efficiency, making them well-suited for real-time applications where both performance and speed are critical.

  • Hybrid models achieved high performance but at the cost of increased execution times, indicating a trade-off between robustness and computational efficiency.

  • Hybrid models, while computationally intensive, also benefit from scaling, demonstrating improved performance. Therefore, for optimal model performance, especially for those models depending on distance metrics, feature scaling is a crucial preprocessing step.

Table 9 presents a comparison of the accuracy of our proposed ensemble model (XGBoost) with the EL models used in previous studies. It is clear that our model consistently outperforms the others in terms of accuracy. The results indicate that XGBoost, as the best-performing model in our approach, achieves superior classification accuracy compared to the ensemble models tested in prior research.

Table 9 Comparison of our ensemble learning technique accuracy (best) with previous studies
Full size table

Despite the promising results, this study has some limitations. The dataset used is suitable for training and evaluation, but it may not fully capture the complexity of real-world network traffic, which could affect performance in dynamic settings. Although techniques like SMOTE were used to address class imbalance, more severe imbalances in practical scenarios could cause additional challenges. Additionally, models like SVM and KNN are sensitive to feature scaling, introducing preprocessing overhead. Finally, hybrid models (SVM-DT and KNN-SVM) may face scalability challenges in real-time applications due to their higher computational demands.

6 Conclusion and Future Work

This paper studied the integration of SDN with ML to enhance TC for QoS optimization in modern network environments. The study covered four scenarios: multiclass classification and binary classification, both before and after scaling. Various ML models, including linear, non-linear, and hybrid models, were evaluated using five metrics which are accuracy, F1 score, kappa score, ROC curve, and confusion matrix. Among the models tested, XGBoost consistently demonstrated the best performance, achieving an accuracy of up to 99.97% across all scenarios. The paper also compared between four different feature scaling methods which are min-max, max-abs, standard, and robust scaling. Min-max and max-abs scaling emerged as the most effective, providing the highest accuracy compared to standard scaling, and robust scaling. Furthermore, the results show that DT and XGBoost provide high accuracy and fast execution, making them ideal for real-time applications. These classification methods optimize QoS in SDN environments by enabling detailed traffic management with multi-class classification and simplifying prioritization with binary classification. Combining both approaches allows SDN administrators to maintain stability and responsiveness under varying network conditions.

In terms of future work, deploying these models in real-world SDN environments could provide valuable insights into their performance under dynamic conditions. It would also be beneficial to extend the work into areas like edge and fog computing, which are becoming increasingly important in modern networks. Moreover, incorporating more advanced learning methods could improve the models’ scalability.