Abstract
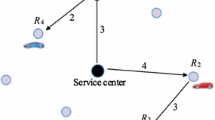
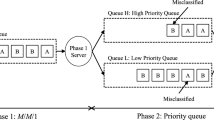
This paper is concerned with a scheduling problem that occurs in service systems where customers are classified as ‘ordinary’ and ‘special’. Ordinary customers can be served on any service facility, while special customers can be served only on the flexible service facilities. Customers arrive dynamically over time and their needs become known upon arrival. We assume any service, once started, will be carried out to its completion. In this paper, we study the worst-case performance of service policies used in practice. In particular, we evaluate three classes of service policies: policies with priority, policies without priority, and their combinations. We obtain tight worst-case performance bounds for all service policies considered.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Ambhl, C., & Mastrolilli, M. (2005). On-line scheduling to minimize max flowtime: an optimal preemptive algorithm. Operations Research Letters, 33, 597–602.
Aspnes, J., Azar, Y., Fiat, A., Plotkin, S., & Waarts, O. (1997). On-line load balancing with applications to machine scheduling and virtual circuit routing. Journal of the Association for Computing Machinery, 44, 486–504.
Azar, Y., Naor, J., & Rom, R. (1995). The competitiveness of on-line assingments. Journal of Algorithms, 18, 221–237.
Bell, S. L., & Williams, R. J. (2001). Dynamic Scheduling of a system with two parallel servers in heavy traffic with resource pooling: asymptotic optimality of a threshold policy. Annals of Applied Probability, 11, 608–649.
Chen, B., Potts, C. N., & Woeiginger, G. J. (1998). A review of machine scheduling: Complexity, algorithm and approximability. In D.-Z. Du & P. Pardalos (Eds.), Handbook of combinatorial optimization (Vol. 3, pp. 21–169). Dordrecht: Kluwer Academic.
Davis, E., & Jaffe, J. M. (1981). Algorithm for scheduling tasks on unrelated processors. Journal of the Association for Computing Machinery, 28, 721–736.
Graham, R. L. (1966). Bounds for certain multiprocessing anomalies. Bell System Technical Journal, 45, 1563–1581.
Hall, L. A., & Shmoys, D. B. (1989). Approximation schemes for constrained scheduling problems. In Proceedings of the 30th IEEE symposium on foundations of computer science (pp. 134–139). Los Alamitos: IEEE Computer Society Press.
Harrison, J. M. (1998). Heavy traffic analysis of a system with parallel servers: asymptotic optimality of discrete-review policies. Annals of Applied Probability, 8, 822–848.
Pruhs, K., Sgall, J., & Torng, E. (2004). Online scheduling. In J.Y.-T. Leung (Ed.), Handbook of scheduling: algorithms, models, and performance analysis (pp. 15.1–15.43). Boca Raton: CRC Press.
Shmoys, D. B., Wein, J., & Williamson, D. P. (1995). Scheduling parallel machines on-line. SIAM Journal on Computing, 24, 1313–1331.
Wang, Z. (2006). Research on on-line service scheduling. PhD dissertation, Department of Mathematical Sciences, Tsinghua University, Beijing, China (in Chinese).
Wang, Z., & Xing, W. (2008, in press). Worst-case analysis for on-line service policies. Journal of Combinatorial Optimization.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wang, Z., Xing, W. & Chen, B. On-line service scheduling. J Sched 12, 31–43 (2009). https://doi.org/10.1007/s10951-008-0075-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10951-008-0075-7