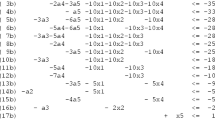Abstract
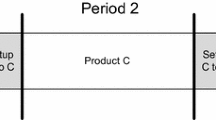
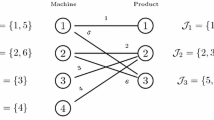
In production planning, sequence dependent setup times and costs are often incurred for switchovers from one product to another. When setup times and costs do not respect the triangular inequality, a situation may occur where the optimal solution includes more than one batch of the same product in a single period—in other words, at least one sub tour exists in the production sequence of that period. By allowing setup crossovers, flexibility is increased and better solutions can be found. In tight capacity conditions, or whenever setup times are significant, setup crossovers are needed to assure feasibility. We present the first linear mixed-integer programming extension for the capacitated lot-sizing and scheduling problem incorporating all the necessary features of sequence sub tours and setup crossovers. This formulation is more efficient than other well known lot-sizing and scheduling models.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Almada-Lobo, B., Klabjan, D., Oliveira, J. F., & Carravilla, M. A. (2007). Single machine multi-product capacitated lot sizing with sequence-dependent setups. International Journal of Production Research, 45(20), 4873–4894.
Balas, E. (1989). The prize collecting traveling salesman problem. Networks, 19(6), 621–636.
Clark, A. R., & Clark, S. J. (2000). Rolling-horizon lot-sizing when set-up times are sequence-dependent. International Journal of Production Research, 38(10), 2287–2307.
Drexl, A., & Kimms, A. (1997). Lot sizing and scheduling—survey and extensions. European Journal of Operational Research, 99(2), 221–235.
Fleischmann, B. (1994). The discrete lot-sizing and scheduling problem with sequence-dependent setup costs. European Journal of Operational Research, 75(2), 395–404.
Fleischmann, B., & Meyr, H. (1997). The general lotsizing and scheduling problem. OR Spektrum, 19, 11–21.
Gopalakrishnan, M. (2000). A modified framework for modelling set-up carry over in the capacitated lotsizing problem. International Journal of Production Research, 38(14), 3421–3424.
Gopalakrishnan, M., Miller, D. M., & Schmidt, C. P. (1995). A framework for modelling setup carryover in the capacitated lot sizing problem. International Journal of Production Research, 33(7), 1973–1988.
Haase, K. (1996). Capacitated lot-sizing with sequence dependent setup costs. OR Spektrum, 18, 51–59.
Haase, K., & Kimms, A. (2000). Lot sizing and scheduling with sequence dependent setup costs and times and efficient rescheduling opportunities. International Journal of Production Economics, 66, 159–169.
Instances (2009). URL http://paginas.fe.up.pt/~balobo/NonTriangular-Setups.
Laporte, G. (1992a). The travelling salesman problem: an overview of exact and approximated algorithms. European Journal of Operational Research, 59(2), 231–248.
Laporte, G. (1992b). The vehicle routing problem: an overview of exact and approximated algorithms. European Journal of Operational Research, 59(2), 345–358.
Porkka, P., & Kuula, A. P. J. V. M. (2000). A modified framework for modelling set-up carryover in the capacitated lotsizing problem. International Journal of Production Research, 38(14), 3421–3424.
Sox, C. R., & Gao, Y. (1999). The capacitated lot sizing problem with setup carry-over. IIE Transactions, 31(2), 173–181.
Suerie, C. (2006). Modeling of period overlapping setup times. European Journal of Operational Research, 174(2), 874–886.
Suerie, C., & Stadtler, H. (2003). The capacitated lot-sizing problem with linked lot sizes. Management Science, 49(8), 1039–1054.
Sung, C., & Maravelias, C. T. (2008). A mixed-integer programming formulation for the general capacitated lot-sizing problem. Computers & Chemical Engineering, 32, 244–259.
Toso, E. A. V., & Morabito, R. (2005). Otimização no dimensionamento e seqüenciamento de lotes de produção: Estudo de caso numa fábrica de rações. Gestão e Produção, 12(2), 203–217.
Wolsey, L. (2002). Solving multi-item lot-sizing problems with an mip solver using classification and reformulation. Management Science, 48(12), 1587–1602.
Zhu, X. Y., & Wilhelm, W. E. (2006). Scheduling and lot sizing with sequence-dependent setup: a literature review. IIE Transactions, 38(11), 987–1007.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Menezes, A.A., Clark, A. & Almada-Lobo, B. Capacitated lot-sizing and scheduling with sequence-dependent, period-overlapping and non-triangular setups. J Sched 14, 209–219 (2011). https://doi.org/10.1007/s10951-010-0197-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10951-010-0197-6