Skip to main content
Springer Nature Link
Log in

New bounds and algorithms for the transshipment yard scheduling problem

  • Published:
Journal of Scheduling Aims and scope Submit manuscript

Abstract

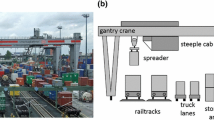
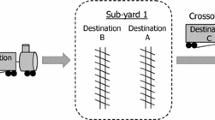
In a modern rail–rail transshipment yard huge gantry cranes transship containers between different freight trains, so that hub-and-spoke railway systems are enabled. In this context, we consider the transshipment yard scheduling problem (TYSP) where trains have to be assigned to bundles, which jointly enter and leave the yard. The objective is to minimize split moves and revisits. Split moves appear whenever containers have to be exchanged between trains of different bundles, whereas revisits occur if a train has to enter the yard twice, because some container dedicated to this train was not available during its first visit. We extend the basic TYSP, so that additional real-world requirements of modern rail–rail yards, e.g., the one currently constructed in Hannover-Lehrte, are considered. We provide complexity proofs for different problem settings and present several heuristic procedures as well as one exact algorithm. The paper concludes with computational results showing the efficiency of the proposed algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Alicke, K. (2002). Modeling and optimization of the intermodal terminal mega hub. OR Spectrum, 24, 1–17.

    Article  Google Scholar 

  • Alicke, K., & Arnold, D. (1998). Modellierung und Optimierung von mehrstufigen Umschlagsystemen. Fördern und Heben, 8, 769–772.

    Google Scholar 

  • Ballis, A., & Golias, J. (2002). Comparative evaluation of existing and innovative rail–road freight transport terminals. Transportation Research Part A: Policy and Practice, 36, 593–611.

    Article  Google Scholar 

  • Blasum, U., Bussieck, M., Hochstättler, W., Moll, C., Scheel, H.-H., & Winter, T. (1999). Scheduling trams in the morning. Mathematical Methods of Operations Research, 49, 137–148.

    Google Scholar 

  • Bontekoning, Y., Macharis, C., & Trip, J. (2004). Is a new applied transportation research field emerging? A review of intermodal rail-truck freight transport literature. Transportation Research Part A: Policy and Practice, 38, 1–24.

    Article  Google Scholar 

  • Bostel, N., & Dejax, P. (1998). Models and algorithms for container allocation problems on trains in a rapid transshipment shunting yard. Transportation Science, 32, 370–379.

    Article  Google Scholar 

  • Boysen, N., & Fliedner, M. (2010). Determining crane areas in intermodal transshipment yards: The yard partition problem. European Journal of Operational Research, 204, 336–342.

    Article  Google Scholar 

  • Boysen, N., Jaehn, F., & Pesch, E. (2010a). Scheduling freight trains in rail–rail transshipment yards, Transportation Science, to apppear

  • Boysen, N., Fliedner, M., & Kellner, M. (2010b). Determining fixed crane areas in rail–rail transshipment yards. Transportation Research Part E, 46, 1005–1016.

    Article  Google Scholar 

  • Cordeau, J.-F., Toth, P., & Vigo, D. (1998). A survey of optimization models for train routing and scheduling. Transportation Science, 32, 380–404.

    Article  Google Scholar 

  • Corry, P., & Kozan, E. (2008). Optimised loading patterns for intermodal trains. OR Spectrum, 30, 721–750.

    Article  Google Scholar 

  • Crainic, T., & Kim, K. (2007). Intermodal transport. In C. Barnhart & G. Laporte (Eds.), Transportation: Vol. 14. Handbooks in operations research and management science (pp. 467–538). Amsterdam: North-Holland.

    Google Scholar 

  • Dahlhaus, E., Horak, P., Miller, M., & Ryan, J. (2000). Optimised loading patterns for intermodal trains. Discrete Applied Mathematics, 103, 41–54.

    Article  Google Scholar 

  • EU (2007). Mitteilung der Kommission an den Rat und das europäische Parlament: Aufbau eines vorrangig für den Güterverkehr bestimmten Schienennetzes.

  • Feo, T., Goldschmidt, O., & Khellaf, M. (1992). One-half approximation algorithms for the k-partition problem. Operations Research, 40, 170–173.

    Article  Google Scholar 

  • Freling, R., Lentink, R., Kroon, L., & Huisman, D. (2005). Shunting of passenger train units in a railway station. Transportation Science, 39, 261–272.

    Article  Google Scholar 

  • Garey, M., & Johnson, D. (1979). Computers and intractability: A guide to the theory of NP-completeness. New York: Freeman.

    Google Scholar 

  • He, S., Song, R., & Chaudhry, S. (2000). Fuzzy dispatching model and genetic algorithms for railyards operations. European Journal of Operational Research, 124, 307–331.

    Article  Google Scholar 

  • Kellner, M., Boysen, N., & Fliedner, M. (2010). How to park freight trains on rail–rail transshipment yards: The train location problem, submitted.

  • Lim, A., Rodrigues, B., & Xu, Z. (2007). A m-parallel crane scheduling problem with a non-crossing constraint. Naval Research Logistics, 54, 115–127.

    Article  Google Scholar 

  • Macharis, C., & Bontekoning, Y. (2004). Opportunities for or in intermodal freight transport research: A review. European Journal of Operational Research, 153, 400–416.

    Article  Google Scholar 

  • Meyer, P. (1999). Entwicklung eines Simulationsprogramms für Umschlagterminals des Kombinierten Verkehrs. Aachen: Shaker Verlag.

    Google Scholar 

  • Moccia, L., Cordeau, J., Gaudioso, M., & Laporte, G. (2006). A branch-and-cut algorithm for the quay crane scheduling problem in a container terminal. Naval Research Logistics, 53, 45–59.

    Article  Google Scholar 

  • Papadimitriou, C., & Steiglitz, K. (1982). Combinatorial optimization: Algorithms and Complexity. Prentice-Hall: Englewood Cliffs.

    Google Scholar 

  • Pesch, E., & Glover, F. (1997). TSP ejection chains. Discrete Applied Mathematics, 76, 165–181.

    Article  Google Scholar 

  • Rotter, H. (2004). New operating concepts for intermodal transport: The mega hub in Hanover/Lehrte in Germany. Transportation Planning and Technology, 27, 347–365.

    Article  Google Scholar 

  • Sammarra, M., Cordeau, J., Laporte, G., & Monaco, M. (2007). A tabu search heuristic for the quay crane scheduling problem. Journal of Scheduling, 10, 327–336.

    Article  Google Scholar 

  • Tanaev, V. S., Gordon, V. S., & Shafransky, Y. M. (1994). Scheduling theory. Single-stage systems. Kluwer: Dordrecht.

    Book  Google Scholar 

  • Wiegmans, B., Stekelenburg, D., Versteegt, C., & Bontekoning, Y. (2007). Modeling rail–rail exchange operations: An analysis of conventional and new-generation terminals. Transportation Journal, 46, 5–20.

    Google Scholar 

  • Winter, T., & Zimmermann, U. (2000). Real-time dispatch of trams in storage yards. Annals of Operations Research, 96, 287–315.

    Article  Google Scholar 

  • Zhu, Y., & Lim, A. (2006). Crane scheduling with non-crossing constraints. Journal of Operational Research Society, 57, 1464–1471.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Lehrstuhl für Allgemeine Betriebswirtschaftslehre/Operations Management, Friedrich-Schiller-Universität Jena, Carl-Zeiß-Straße 3, 07743, Jena, Germany

    Nils Boysen

  2. Institut für Wirtschaftsinformatik, Universität Siegen, Hölderlinstraße 3, 57068, Siegen, Germany

    Florian Jaehn & Erwin Pesch

Authors
  1. Nils Boysen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Florian Jaehn
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Erwin Pesch
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Erwin Pesch.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Boysen, N., Jaehn, F. & Pesch, E. New bounds and algorithms for the transshipment yard scheduling problem. J Sched 15, 499–511 (2012). https://doi.org/10.1007/s10951-010-0200-2

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10951-010-0200-2

Keywords