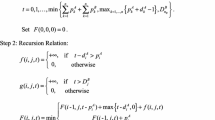Abstract
We consider the competitive multi-agent scheduling problem on a single machine, where each agent’s cost function is to minimize its total weighted late work. The aim is to find the Pareto-optimal frontier, i.e., the set of all Pareto-optimal points. When the number of agents is arbitrary, the decision problem is shown to be unary \(\mathcal {NP}\)-complete even if all jobs have the unit weights. When the number of agents is two, the decision problems are shown to be binary \(\mathcal {NP}\)-complete for the case in which all jobs have the common due date and the case in which all jobs have the unit processing times. When the number of agents is a fixed constant, a pseudo-polynomial dynamic programming algorithm and a \((1+\epsilon )\)-approximate Pareto-optimal frontier are designed to solve it.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Agnetis, A., Billaut, J. C., Gawiejnowicz, S., Pacciarelli, D., & Souhal, A. (2014). Multiagent scheduling: Models and algorithms. Berlin: Springer.
Agnetis, A., Mirchandani, P. B., Pacciarelli, D., & Pacifici, A. (2004). Scheduling problems with two competing agents. Operations Research, 52, 229–242.
Agnetis, A., Pacciarelli, D., & Pacifici, A. (2007). Multi-agent single machine scheduling. Annals of Operations Research, 150, 3–15.
Arbib, C., Smriglio, S., & Servilio, M. (2004). A competitive scheduling problem and its relevance to UMTS channel assignment. Networks, 44, 132–141.
Baker, K. R., & Smith, J. C. (2003). A multiple-criterion model for machine scheduling. Journal of Scheduling, 6, 7–16.
Blazewicz, J. (1984). Scheduling preemptible tasks on parallel processors with information loss. Technique et Science Informatiques, 3, 415–420.
Blazewicz, J., Pesch, E., Sterna, M., & Werner, F. (2004). Open shop scheduling problems with late work criteria. Discrete Applied Mathematics, 134, 1–24.
Blazewicz, J., Pesch, E., Sterna, M., & Werner, F. (2005). The two-machine flow-shop problem with weighted late work criterion and common due date. European Journal of Operational Research, 165, 408–415.
Blazewicz, J., Pesch, E., Sterna, M., & Werner, F. (2007). A note on two-machine job shop with weighted late work criterion. Journal of Scheduling, 10, 87–95.
Chen, R. B., Yuan, J. J., & Gao, Y. (2019a). The complexity of CO-agent scheduling to minimize the total completion time and total number of tardy jobs. Journal of Scheduling, 22, 581–593.
Chen, R. B., Yuan, J. J., Ng, C. T., & Cheng, T. C. E. (2019b). Single-machine scheduling with deadlines to minimize the total weighted late work. Naval Research Logistics, 66, 582–595.
Chen, X., Chau, V., Xie, P., Sterna, M., & Blazewicz, J. (2017). Complexity of late work minimization in flow shop systems and a particle swarm optimization algorithm for learning effect. Computers and Industrial Engineering, 111, 176–182.
Chen, X., Sterna, M., Han, X., & Blazewicz, J. (2016). Scheduling on parallel identical machines with late work criterion: Offline and online cases. Journal of Scheduling, 19, 729–736.
Cheng, T. C. E., Ng, C. T., & Yuan, J. J. (2006). Multi-agent scheduling on a single machine to minimize total weighted number of tardy jobs. Theoretical Computer Science, 362, 273–281.
Garey, M. R., & Johnson, D. S. (1979). Computers and intractability: A guide to the theory of \(\cal{NP}\)-completeness. San Francisco: Freeman.
Gerstl, E., Mor, B., & Mosheiov, G. (2019). Scheduling on a proportionate flowshop to minimize total late work. International Journal of Production Research, 57, 531–543.
Hariri, A. M. A., Potts, C. N., & Van Wassenhove, L. N. (1995). Single machine scheduling to minimize total late work. ORSA Journal on Computing, 7, 232–242.
Kovalyov, M. Y., Oulamara, A., & Soukhal, A. (2015). Two-agent scheduling with agent specific batches on an unbounded serial batching machine. Journal of Scheduling, 18, 423–434.
Kovalyov, M. Y., Potts, C. N., & Van Wassenhove, L. N. (1994). A fully polynomial approximation scheme for scheduling a single machine to minimize total weighted late work. Mathematics of Operations Research, 19, 86–93.
Lee, K., Choi, B. C., Leung, J. Y. T., & Pinedo, M. (2009). Approximation algorithms for multi-agent scheduling to minimize total weighted completion time. Information Processing Letters, 109, 913–917.
Leung, J. Y. T. (2004). Minimizing total weighted error for imprecise computation tasks and related problems. In J. Y. Leung (Ed.), Handbook of scheduling: Algorithms, models, and performance analysis. Boca Raton: Chapman and Hall/CRC.
Leung, J. Y. T., Pinedo, M., & Wan, G. (2010). Competitive two-agent scheduling and its applications. Operations Research, 58, 458–469.
Li, S. S., Chen, R. X., & Li, W. J. (2018). Proportionate flow shop scheduling with multi-agents to maximize total gains of JIT jobs. Arabian Journal for Science and Engineering, 43, 969–978.
Liu, S. C., Duan, J., Lin, W. C., Wu, W. H., Kung, J. K., Chen, H., et al. (2018). A branch-and-bound algorithm for two-agent scheduling with learning effect and late work criterion. Asia-Pacific Journal of Operational Research, 35, 1850037.
Ng, C. T., Cheng, T. C. E., & Yuan, J. J. (2006). A note on the complexity of the problem of two-agent scheduling on a single machine. Journal of Combinatorial Optimization, 12, 387–394.
Oron, D., Shabtay, D., & Steiner, G. (2015). Single machine scheduling with two competing agents and equal job processing times. European Journal of Operational Research, 244, 86–99.
Papadimitriou C, Yannakakis M (2000) On the approximability of trade-offs and optimal access of web sources. In Proceedings of the 41st annual IEEE symposium on the foundations of computer science (pp 86–92).
Perez-Gonzalez, P., & Framinan, J. M. (2014). A common framework and taxonomy for multicriteria scheduling problems with interfering and competing jobs: Multi-agent scheduling problems. European Journal of Operational Research, 235, 1–16.
Piroozfard, H., Wong, K. Y., & Wong, W. P. (2018). Minimizing total carbon footprint and total late work criterion in flexible job shop scheduling by using an improved multi-objective genetic algorithm. Resources, Conservation and Recycling, 128, 267–283.
Potts, C. N., & Van Wassenhove, L. N. (1991). Single machine scheduling to minimize total late work. Operations Research, 40, 586–595.
Potts, C. N., & Van Wassenhove, L. N. (1992). Approximation algorithms for scheduling a single machine to minimize total late work. Operations Research Letters, 11, 261–266.
Shioura, A., Shakhlevich, N. V., & Strusevich, V. A. (2018). Preemptive models of scheduling with controllable processing times and of scheduling with imprecise computation: A review of solution approaches. European Journal of Operational Research, 266, 795–818.
Sterna, M. (2011). A survey of scheduling problems with late work criteria. Omega, 39, 120–129.
Sterna, M., & Czerniachowska, K. (2017). Polynomial time approximation scheme for two parallel machines scheduling with a common due date to maximize early work. Journal of Optimization Theory and Applications, 174, 927–944.
Wang, D. J., Kang, C. C., Shiau, Y. R., Wu, C. C., & Hsu, P. H. (2017). A two-agent single-machine scheduling problem with late work criteria. Soft Computing, 21, 2015–2033.
Yin, Y., Wang, W., Wang, D., & Cheng, T. C. E. (2017). Multi-agent single-machine scheduling and unrestricted due date assignment with a fixed machine unavailability interval. Computers & Industrial Engineering, 111, 202–215.
Yin, Y., Xu, J., Cheng, T. C. E., Wu, C. C., & Wang, D. J. (2016). Approximation schemes for single-machine scheduling with a fixed maintenance activity to minimize the total amount of late work. Naval Research Logistics, 63, 172–183.
Yuan, J. J. (2016). Complexities of some problems on multi-agent scheduling on a single machine. Journal of the Operations Research Society of China, 4, 379–384.
Yuan, J. J. (2017). Multi-agent scheduling on a single machine with a fixed number of competing agents to minimize the weighted sum of number of tardy jobs and makespans. Journal of Combinatorial Optimization, 34, 433–440.
Yuan, J. J., Ng, C. T., & Cheng, T. C. E. (2020). Scheduling with release dates and preemption to minimize multiple max-form objective functions. European Journal of Operational Research, 280, 860–875.
Zhang, X., & Wang, Y. (2017). Two-agent scheduling problems on a single-machine to minimize the total weighted late work. Journal of Combinatorial Optimization, 33, 945–955.
Zhang, Y., & Yuan, J. J. (2019). A note on a two-agent scheduling problem related to the total weighted late work. Journal of Combinatorial Optimization, 37, 989–999.
Acknowledgements
We would like to thank the Associate Editor and four anonymous referees for their helpful comments and suggestions on an earlier version of this paper. Li was supported in part by the Key Research Projects of Henan Higher Education Institutions (20A110037) and the Young Backbone Teachers Training Program of Zhongyuan University of Technology. Yuan was supported in part by National Natural Science Foundation of China under Grant Numbers (11671368, 11771406).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Example
Consider a two-agent scheduling problem \(1 | CO | \mathcal {P}(\sum w_j^{(1)}Y_j^{(1)}, \sum w_j^{(2)}Y_j^{(2)})\), in which \(\mathcal {J}^1=\{J_1^{(1)}, J_2^{(1)}\}\), \(\mathcal {J}^2=\{J_1^{(2)}, J_2^{(2)}, J_3^{(2)}\}\), and the corresponding job parameters are given in Table 1.
Before executing algorithm \(\mathcal {H}_1\), the jobs are first indexed in the EDD order, see Table 2.
In the sequel, we apply algorithm \(\mathcal {H}_1\) to solve this numerical example.
Step 1 [Initialization] Set \(\mathcal {L}_0=\{(0, 0, 0, 0, 0)\}\), \({\mathcal L}_j=\emptyset \) for \(j=1, 2, \ldots , 5\) and \(j:=0\).
Step 2 [Generation] For \(j=1\), \(\mathcal {L}_1=\{(1, 0, 2, 0, 0)\), \((1, 0, 0, 0, 1), (1, 2, 0, 0, 0)\}\), see Table 3 for the generation process.
For \(j=2\), \(\mathcal {L}_2=\{(2, 0, 2, 6, 0), (2, 0, 2, 0, 2), (2, 3, 2, 0, 0)\), \((2, 0, 0, 6, 1), (2, 2, 0, 6, 0), (2, 2, 0, 0, 2), (2, 5, 0, 2, 0)\}\), see Table 4 for the generation process.
For \(j=3\), \(\mathcal {L}_3=\{(3, 0, 14, 6, 0), (3, 0, 2, 6, 3),\)\((3, 4, 2, 6, 0), (3, 0, 14, 0, 2),\) (3, 3, 14, 0, 0), (3, 3, 2, 0, 3), \((3, 7, 2, 0, 0),\) (3, 0, 12, 6, 1), (3, 2, 12, 6, 0), \((3, 2, 0, 6, 3), (3, 6, 0, 6, 0),\) (3, 2, 12, 0, 2), \((3, 5, 12, 2, 0), (3, 5, 0, 2, 3), (3, 9, 6, 2, 0)\}\), see Table 5 for the generation process.
For \(j=4\), \(\mathcal {L}_4=\{(4, 0, 14, 14, 0), (4, 0, 14, 6, 4),\) (4, 2, 14, 6, 0), (4, 0, 2, 14, 3), (4, 2, 2, 6, 3), \((4, 6, 2, 6, 0), (4, 4, 2, 14, 0), (4, 4, 2, 6, 4),\)\((4, 0, 14, 8, 2), (4, 2, 14, 0, 2), (4, 3, 14, 0, 4),\) (4, 5, 14, 0, 0), (4, 5, 2, 0, 3), (4, 9, 8, 0, 0), (4, 0, 12, 14, 1), (4, 2, 12, 6, 1), \((4, 2, 12, 14, 0), (4, 2, 12, 6, 4), (4, 4, 12, 6, 0)\), \((4, 2, 0, 14, 3), (4, 4, 0, 6, 3), (4, 6, 0, 14, 0),\) (4, 6, 0, 6, 4), (4, 8, 0, 10, 0), \((4, 2, 12, 8, 2), (4, 5, 12, 2, 4), (4, 7, 12, 2, 0)\}\), see Table 6 for the generation process, where the underlined states are eliminated in Step 2.2.
For \(j=5\), \(\mathcal {L}_5=\{(5, 0, 14, 23, 0), (5, 3, 14, 14, 0),\) (5, 2, 14, 15, 0), (5, 5, 14, 6, 0), (5, 9, 8, 6, 0), \((5, 4, 2, 23, 0), (5, 7, 2, 14, 0),\) (5, 6, 2, 15, 0), (5, 9, 2, 12, 0), \((5, 8, 14, 3, 0), (5, 7, 2, 14, 0),\) (5, 2, 12, 23, 0), (5, 5, 12, 14, 0), (5, 4, 12, 15, 0), (5, 7, 12, 6, 0), (5, 6, 0, 23, 0), \((5, 8, 0, 19, 0)\}\), see Table 7 for the generation process (note that we do not need to consider the case where job \(J_5\) is deferred as it is the last job), where the underlined states are eliminated in Step 2.2.
Step 3 [Refinement] \(\mathcal {L}_5=\{(5, 8, 0, 19, 0), (5, 9, 2, 12, 0),\)\((5, 9, 8, 6, 0), (5, 8, 14, 3, 0)\}\).
Step 4 [Result] The Pareto-optimal frontier is \(\mathcal {R}=\{(0, 19), (2, 9),\)\((8, 6), (14, 3)\}\).
-
The Pareto-optimal schedule corresponding to (0, 19) is \(J_1^{(1)} \prec J_2^{(1)} \prec J_2^{(2)} \prec \underline{J_1^{(2)}} \prec \underline{J_3^{(2)}}\);
-
The Pareto-optimal schedule corresponding to (2, 12) is \(J_2^{(1)} \prec J_2^{(2)} \prec J_3^{(2)} \prec \underline{J_1^{(1)}} \prec \underline{J_1^{(2)}}\);
-
The Pareto-optimal schedule corresponding to (8, 6) is \(J_2^{(2)} \prec J_3^{(2)} \prec J_2^{(1)} \prec \underline{J_1^{(1)}} \prec \underline{J_1^{(2)}}\);
-
The Pareto-optimal schedule corresponding to (14, 3) is \(J_1^{(2)} \prec J_2^{(2)} \prec J_3^{(2)} \prec \underline{J_1^{(1)}} \prec \underline{J_2^{(1)}}\);
where the underlined jobs are late in the corresponding Pareto-schedule.
Rights and permissions
About this article
Cite this article
Li, SS., Yuan, JJ. Single-machine scheduling with multi-agents to minimize total weighted late work. J Sched 23, 497–512 (2020). https://doi.org/10.1007/s10951-020-00646-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10951-020-00646-7