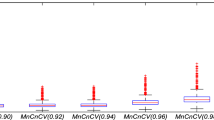
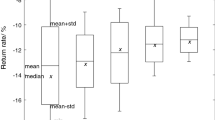
Abstract
Conditional Value at Risk (CVaR) has been recently used to approximate a chance constraint. In this paper, we study the convergence of stationary points, when sample average approximation (SAA) method is applied to a CVaR approximated joint chance constrained stochastic minimization problem. Specifically, we prove under some moderate conditions that optimal solutions and stationary points, obtained from solving sample average approximated problems, converge with probability one to their true counterparts. Moreover, by exploiting the recent results on large deviation of random functions and sensitivity results for generalized equations, we derive exponential rate of convergence of stationary points. The discussion is also extended to the case, when CVaR approximation is replaced by a difference of two convex functions (DC-approximation). Some preliminary numerical test results are reported.



Similar content being viewed by others
References
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Ben-Tal, A., Nemirovski, A.: Robust solutions of linear programming problems contaminated with uncertain data. Math. Program. 88, 411–424 (2000)
Rockafellar, R.T., Uryasev, S.: Optimization of conditional value-at-risk. J. Risk 2, 21–41 (2000)
Nemirovski, A., Shapiro, A.: Convex approximations of chance constrained programs. SIAM J. Optim. 17, 969–996 (2006)
Robinson, S.M.: Analysis of sample-path optimization. Math. Oper. Res. 21, 513–528 (1996)
Shapiro, A.: Monte Carlo sampling methods. In: Rusczyński, A., Shapiro, A. (eds.) Stochastic Programming. Handbooks in OR & MS, vol. 10. North-Holland, Amsterdam (2003)
Xu, H., Zhang, D.: Smooth sample average approximation of stationary points in nonsmooth stochastic optimization and applications. Math. Program. 119, 371–401 (2009)
Meng, F.W., Sun, J., Goh, M.: Stochastic optimization problems with CVaR risk measure and their sample average approximation. J. Optim. Theory Appl. 146, 399–418 (2010)
Hiriart-Urruty, J.B.: Refinements of necessary optimality conditions in nondifferentiable programming I. Appl. Math. Optim. 5, 63–82 (1979)
Pflug, G.Ch.: Stochastic optimization and statistical inference. In: Rusczyński, A., Shapiro, A. (eds.) Stochastic Programming. Handbooks in OR & MS, vol. 10. North-Holland, Amsterdam (2003)
Shapiro, A., Xu, H.: Stochastic mathematical programs with equilibrium constraints, modeling and sample average approximation. Optimization 57, 395–418 (2008)
Xu, H.: Uniform exponential convergence of sample average random functions under general sampling with applications in stochastic programming. J. Math. Anal. Appl. 368, 692–710 (2010)
Sun, H., Xu, H.: A note on uniform exponential convergence of sample average approximation of random functions. J. Math. Anal. Appl. 385, 698–708 (2012)
Hong, L.J., Yang, Y., Zhang, L.: Sequential convex approximations to joint chance constrained programs: a Monte Carlo approach. Oper. Res. 59, 617–630 (2011)
Clarke, F.H.: Optimization and Nonsmooth Analysis. Wiley, New York (1983)
Wang, W.: Sample average approximation of risk-averse stochastic programs. PhD Thesis, Georgia Institute of Technology (2007)
Aumann, R.J.: Integrals of set-valued functions. J. Math. Anal. Appl. 12, 1–12 (1965)
Artstein, Z., Vitale, R.A.: A strong law of large numbers for random compact set. Ann. Probab. 3, 879–882 (1975)
Bonnans, J.F., Shapiro, A.: Perturbation Analysis of Optimization Problems. Springer Series in Operations Research. Springer, New York (2000)
Berge C, C.: Espaces Topologiques, Fonctions Multivoques. Dunod, Paris (1966)
Dentcheva, D., Ruszczyński, A.: Composite semi-infinite optimization. Control Cybern. 36, 1–14 (2007)
Sun, H., Xu, H.: Convergence analysis of stationary points in sample average approximation of stochastic programs with second order stochastic dominance constraints. Math. Program. Ser. B (2012, to appear)
Ralph, D., Xu, H.: Asymptotic analysis of stationary points of sample average two stage stochastic programs: a generalized equation approach. Math. Oper. Res. 36, 568–592 (2011)
Castaing, C., Valadier, M.: Convex Analysis and Measurable Multifunctions. Springer Series in Lecture Notes in Mathematics. Springer, Berlin (1977)
Terán, P.: On a uniform law of large numbers for random sets and subdifferentials of random functions. Stat. Probab. Lett. 78, 42–49 (2008)
Qi, L., Shapiro, A., Ling, C.: Differentiability and semismoothness properties of integral functions and their applications. Math. Program. 102, 223–248 (2005)
Hess, C.: Conditional expectation and martingales of random sets. Pattern Recognit. 32, 1543–1567 (1999)
Papageorgiou, N.S.: On the theory of Banach space valued multifunctions, I: integration and conditional expectation. J. Multivar. Anal. 17, 185–206 (1985)
Rockafellar, R.T., Wets, R.J.-B.: Variational Analysis. Springer, Berlin (1998)
Hong, L.J., Zhang, L.: CVaR approximation to chance constrained program: what is lost and how to find it back? Report, The Hong Kong University of Science and Technology (2010)
Sun, H., Xu, H., Wang, Y.: Asymptotic analysis of sample average approximation for stochastic optimization problems with joint chance constraints via CVaR/DC approximations. Optimization online, old version (2012)
Pflug, C.C., Römisch, W.: Modeling, Measuring and Managing Risk. World Scientific, Singapore (2007)
Conego, A.J., Carrión, M., Morales, J.M.: Decision Making Under Uncertainty in Electricity Markets. Springer, New York (2010)
Alexander, G.J., Baptista, A.M.: A comparison of VaR and CVaR constraints on portfolio selection with the mean-variance model. Manag. Sci. 50, 1261–1273 (2004)
Acknowledgements
The work of H. Sun is carried out while he is visiting H. Xu in the School of Mathematics, University of Southampton sponsored by China Scholarship Council. The authors would like to thank Dr. Yi Yang for helpful discussions of the algorithm of the DC-approximation method. They would also like to thank two anonymous referees for insightful comments which have substantially helped improve the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
In this Appendix, we strengthen [13, Theorem 3.1] by weakening a boundedness condition imposed on the random function.
Theorem 8.1
Let ϕ:ℝn×Ξ→ℝ be a real valued lower semicontinuous function, ξ:Ω→Ξ⊂ℝk a random vector defined on probability space \((\varOmega,\mathcal{F},P)\) and \(\psi(x):=\mathbb {E}[\phi(x,\xi)]\). Let \(\mathcal {X}\subset \mathbb {R}^{n}\) be a compact subset of ℝn. Assume: \(\mathrm{(a)}\) for every \(x\in \mathcal {X}\) the moment generating function \(M_{x}(t):=\mathbb {E}\{e^{t[\phi(x,\xi)-\psi(x)]} \} \) is finite valued for all t in a neighborhood of zero. \(\mathrm{(b)}\) ψ(x) is continuous on \(\mathcal {X}\), (c) ϕ(x,ξ) is bounded by an integrable function L(ξ) and the moment generating function \(\mathbb {E}[e^{(L(\xi)-\mathbb {E}[L(\xi )])t} ]\) is finite valued for t close to 0. Then the following statements hold.
-
(i)
If ϕ(⋅,ξ) is almost H-clam from above at every point \(x\in \mathcal {X}\) with modulus κ x (ξ) and order γ x , and the moment generating function \(\mathbb {E}[e^{\kappa_{x}(\xi)t}]\) is finite valued for t close to 0, then for every ϵ>0, there exist positive constants c(ϵ) and β(ϵ), independent of N, such that
$$ \operatorname {Prob}\Bigl\{\sup_{x\in \mathcal {X}}\bigl(\psi_N(x)-\psi(x) \bigr)\geq \epsilon \Bigr\}\leq c(\epsilon)e^{-N\beta(\epsilon)}. $$(39) -
(ii)
If ϕ(⋅,ξ) is almost H-clam from below at every point \(x\in \mathcal {X}\) with modulus κ x (ξ) and order γ x , and the moment generating function \(\mathbb {E}[e^{\kappa_{x}(\xi)t}]\) is finite valued for t close to 0, then for every ϵ>0, there exist positive constants c(ϵ) and β(ϵ), independent of N, such that
$$ \operatorname {Prob}\Bigl\{\sup_{x\in \mathcal {X}}\bigl(\psi_N(x)-\psi(x)\bigr)\leq- \epsilon \Bigr\}\leq c(\epsilon)e^{-N\beta(\epsilon)}. $$(40) -
(iii)
If ϕ(⋅,ξ) is almost H-clam at every point \(x\in \mathcal {X}\) with modulus κ x (ξ) and order γ x , and the moment generating function \(\mathbb {E}[e^{\kappa_{x}(\xi)t}]\) is finite valued for t close to 0, then for every ϵ>0, there exist positive constants c(ϵ) and β(ϵ), independent of N, such that
$$ \operatorname {Prob}\Bigl\{\sup_{x\in \mathcal {X}}\bigl|\psi_N(x)-\psi(x)\bigr|\geq\epsilon \Bigr\}\leq c(\epsilon)e^{-N\beta(\epsilon)}. $$(41)
Due to the limitation of the length of the paper, we omit the proof which can be found in [31].
Note that the exponential convergence is derived for the case when ξ satisfies a continuous distribution. In the case when ξ satisfies a discrete distribution, the concept of almost H-calmness is no longer applicable. However, the uniform exponential convergence may be established in an entirely different way for a class of random function which is uniformly bounded over a considered compact set. We leave this to interested readers.
Rights and permissions
About this article
Cite this article
Sun, H., Xu, H. & Wang, Y. Asymptotic Analysis of Sample Average Approximation for Stochastic Optimization Problems with Joint Chance Constraints via Conditional Value at Risk and Difference of Convex Functions. J Optim Theory Appl 161, 257–284 (2014). https://doi.org/10.1007/s10957-012-0127-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-012-0127-1