Necessary and Sufficient Conditions for Feedback Nash Equilibria for the Affine-Quadratic Differential Game

Abstract

In this note, we consider the non-cooperative linear feedback Nash quadratic differential game with an infinite planning horizon. The performance function is assumed to be indefinite and the underlying system affine. We derive both necessary and sufficient conditions under which this game has a Nash equilibrium. As a special case, we derive existence conditions for the multi-player zero-sum game.

Appendix A

Lemma A.1

Let S:=BR ⁻¹ B ^T and c(.,x ₀),p(⋅)∈L ₂. Consider the minimization of the linear-quadratic cost function

(9)

subject to the state dynamics

$$ \dot{x}(t) = A x(t) + B u(t) + c(t,x_0), \quad x(0)=x_0, $$

(10)

and $u \in \mathcal{U}_{s}(x_{0})$. Then,

• (a) with c(⋅)=p(⋅)=0, (9)–(10) has a solution for all x ₀∈ℝⁿ if and only if the algebraic Riccati equation

  

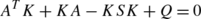  (11)

  has a symmetric stabilizing solution K(⋅) (i.e. A−SK is a stable matrix).

• (b) for every x ₀, problem (9)–(10) has a solution iff. Equation (11) has a stabilizing solution. Moreover if (11) has a stabilizing solution then problem (9)–(10) has the unique solution u ^∗(t)=−R ⁻¹ B ^T(Kx ^∗(t)+h(t)). Here h(t) is given by $h(t)=\int_{t}^{\infty}e^{-(A-SK)^{T}(t-s)}(Kc(s)+p(s))\,ds$, and x ^∗(t) satisfies $\dot{x}^{*}(t)=(A-SK)x^{*}(t)-Sh(t)+c(t), x^{*}(0)=x_{0}$.

Proof

Similar to the proof of [21, Theorem 5.16]. □

Proof of Theorem 3.1

⇒ part. Let u ^∗ be a FNE. Then, for all t ₀≥0, $\lim_{t_{f}\rightarrow \infty} J_{i}(t_{0}, t_{f}, x_{0},u^{*}) \leq \lim_{t_{f}\rightarrow \infty} J_{i}(t_{0},t_{f},x_{0},u_{-i}^{*}(\alpha))$ for every x ₀ and input α such that $u_{-i}^{*}(\alpha) \in \mathcal{U}_{s}$. Let t ₀ be fixed. Consequently, with $\bar{M}_{i}:=M_{i}-M_{i}E_{i+1}R_{ii}^{-1}E_{i+1}^{T}M_{i}$, for every x ₀∈ℝⁿ the minimization of

(12)

subject to the state equation

has a solution. Straightforward calculations show that $\bar{M}_{i}$ is in the kernel of $E_{i+1}^{T}$. Therefore, with

(13)

the above minimization problem can be rewritten as the minimization of

(14)

subject to the (nonhomogeneous) state equation

(15)

Let $S_{i}:=B_{i}R_{ii}^{-1}B_{i}^{T}$ and $\bar{A}_{i}:=A+B_{-i}F_{-i}^{*}-B_{i}R_{ii}^{-1}E_{i+1}^{T}M_{i}[I\ F_{-i}^{*^{T}}]^{T}-S_{i}K_{i}$. Then, by Lemma A.1, it follows that (16) below has a stabilizing solution:

(16)

According Lemma A.1 the minimization problem (14)–(15) has the unique solution

(17)

where

and K _i is the stabilizing solution of (16). So, by (13), $\tilde{u}_{i}(t)$ below solves problem (12).

(18)

Since the optimal control for this problem is uniquely determined and, by definition, the equilibrium control $u_{i}^{*}=F_{i}^{*}x(t)+g_{i}^{*}(t)$ solves the optimization problem, it follows that

(19)

Consequently, ∀i, $\bar{A}_{i}=A+BF^{*}=:A_{\mathrm{cl}}$. Furthermore, by (19),

or

Similarly, by (19), $R_{ii}g_{i}^{*}+E_{i+1}^{T}M_{i}[0\ g_{-i}^{*^{T}}(t)]^{T}=-B_{i}^{T}h_{i}(t)$. Therefore

Furthermore, notice from (19) that $-R_{ii}^{-1}E_{i+1}^{T}M_{i}[I\ F_{-i}^{*^{T}}]^{T}=F_{i}^{*}+R_{ii}^{-1}B_{i}^{T}K_{i}$. So,

$$ \bigl[A+B_{-i}F_{-i}^{*}-B_iR_{ii}^{-1}E_{i+1}^{T}M_i \bigl[I\ F_{-i}^{*^T} \bigr]^T \bigr]^TK_i = A_\mathrm{cl}^TK_i+K_iS_iK_i. $$

(20)

On the other hand, by (19), $-R_{ii}^{-1}B_{i}^{T}K_{i}=F_{i}^{*}+R_{ii}^{-1}E_{i+1}^{T}M_{i}[I\ F_{-i}^{*^{T}}]^{T}$. Substitution of this into $K_{i}S_{i}K_{i}=(R_{ii}^{-1}B_{i}^{T}K_{i})^{T}R_{ii}R_{ii}^{-1}B_{i}^{T}K_{i}$ yields then the result, together with (20), that (16) can be rewritten as (4). Next, reconsider h _i (t). Substitution of n _i (s) and p _i (s) into (17) shows that

(21)

Pre-multiplication of (19) by M _i E _i+1 shows that

Using this, h _i (t) from (21) can be rewritten as

Since $g_{-i}^{*}=I_{N,-i}g^{*}=-I_{N,-i}G^{-1}\tilde{B}^{T}h(t)$, (5) results. As σ(A _cl)⊂ℂ⁻ and c(⋅)∈L ² it follows from, e.g., [27, Theorem 2.1.1] that (5) has a unique solution.

⇐ part. Let K be a stabilizing solution of (4) and define, for i≠1, $u_{i}^{*}:=(F^{*}_{i},g_{i}^{*})$ by (3)–(5). Next, without loss of generality, consider for a fixed t ₀ the minimization by player one of the cost functional

subject to the system $\dot{x}(t)=(A+B_{-1}F_{-1}^{*})x(t)+B_{1}u_{1}(t)+B_{-1}g_{-1}^{*}(t)+c(t), x(t_{0})=x_{0}$. By the “⇒ part” the problem can be rewritten as the minimization of (14) subject to (15). From (3) it follows (see, e.g., (19) again) that (4) can be rewritten as (16). Taking i=1 in (16) shows that the ARE (22), below, has a stabilizing solution K=K ₁:

(22)

But this implies, by Lemma A.1, that the minimization of (14) subject to (15) has a solution. By the “⇒ part” its solution is (17). So, using (3), the optimal control for player one is

So, in particular at time t=t ₀, $(F_{1}^{*},g_{1}^{*}(t_{0}))$ is the optimal response of player one in case all other players i use the control strategy $(F_{i}^{*},g_{i}^{*}(t_{0}))$. Since the closed-loop system is $\dot{x}(t)=A_{\mathrm{cl}}x(t)+Bg(t)+c(t)$, with v(s):=(2x ^T(s)[I F ^T]+[0 g ^T(s)])M _i [0 g ^T(s)]^T, J _i can be rewritten as

 □

Proof of Corollary 3.1

Since σ(H)⊂ℂ⁺, h(t) in (7) is well-defined. Differentiation of (7) shows that h(t) satisfies (6). Using (6) the right-hand side of (5) can be rewritten as

So, h(t) satisfies (5). Since (5) has a unique solution, this concludes the proof. □