Skip to main content

Advertisement

Springer Nature Link
Log in

An Optimal Family of Fast 16th-Order Derivative-Free Multipoint Simple-Root Finders for Nonlinear Equations

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

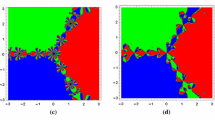
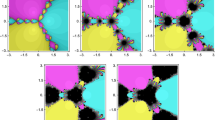
This paper investigates an optimal family of derivative-free fast 16th-order multipoint iterative methods for solving nonlinear equations using polynomial weighting functions and a real control parameter. Convergence analyses and computational properties are shown along with a comparison of the classical work done by Kung–Traub in 1974. The underlying theoretical treatment and computational advantage of faster computing time is well supported through a variety of concrete numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Kung, H.T., Traub, J.F.: Optimal order of one-point and multipoint iteration. J. ACM 21, 643–651 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  2. Chen, M., Chang, T.-S.: On the higher-order method for the solution of a nonlinear scalar equation. J. Optim. Theory Appl. 149, 647–664 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  3. Germani, A., Manes, C., Palumbo, P.: Higher-order method for the solution of a nonlinear scalar equation. J. Optim. Theory Appl. 131, 347–364 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  4. Geum, Y.H., Kim, Y.I.: A multi-parameter family of three-step eighth-order iterative methods locating a simple root. Appl. Math. Comput. 215(9), 3375–3382 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  5. Geum, Y.H., Kim, Y.I.: A penta-parametric family of fifteenth-order multipoint methods for nonlinear equations. Appl. Math. Comput. 217(6), 2311–2319 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  6. Geum, Y.H., Kim, Y.I.: A biparametric family of eighth-order methods with their third-step weighting function decomposed into a one-variable linear fraction and a two-variable generic function. Comput. Math. Appl. 61(3), 708–714 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  7. Geum, Y.H., Kim, Y.I.: A uniparametric family of three-step eighth-order multipoint iterative methods for simple roots. Appl. Math. Lett. 24(6), 929–935 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  8. Heydari, M., Hosseini, S.M., Loghmani, G.B.: Two new families of iterative methods for solving nonlinear equations with optimal order. Appl. Anal. Discrete Math. 5, 93–109 (2011)

    Article  MathSciNet  Google Scholar 

  9. Kim, Y.I.: A triparametric family of three-step optimal eighth-order methods for solving nonlinear equations. Int. J. Comput. Math. 89(8), 1051–1059 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  10. King, R.F.: Family of fourth-order methods for nonlinear equations. SIAM J. Numer. Anal. 10, 876–879 (1973)

    Article  MATH  MathSciNet  Google Scholar 

  11. Lee, M.-Y., Kim, Y.I.: A family of fast derivative-free fourth-order multipoint optimal methods for nonlinear equations. Int. J. Comput. Math. 89(15), 2081–2093 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  12. Lu, Y., Xu, X.: A new family of modified Newton methods with cubic convergence. Fixed Point Theory 8, 47–57 (2007)

    MATH  MathSciNet  Google Scholar 

  13. Özban, A.Y.: Some new variants of Newton’s method. Appl. Math. Lett. 17, 677–682 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  14. Peng, Y., Feng, H., Li, Q., Zhang, X.: A fourth-order derivative-free algorithm for nonlinear equations. J. Comput. Appl. Math. 235(8), 2551–2559 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  15. Sargolzaei, P., Soleymani, F.: Accurate fourteenth-order methods for solving nonlinear equations. Numer. Algorithms 578, 513–527 (2011)

    Article  MathSciNet  Google Scholar 

  16. Soleymani, F.: Regarding the accuracy of optimal eighth-order methods. Math. Comput. Model. 53(5–6), 1351–1357 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  17. Soleymani, F., Sharma, R., Li, X., Tohidi, E.: An optimized derivative-free form of the Potra–Pták method. Math. Comput. Model. 56, 97–104 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  18. Soleymani, F., Vanani, S.K., Khan, M., Sharifi, M.: Some modifications of King’s family with optimal eighth order of convergence. Math. Comput. Model. 55, 1373–1380 (2012)

    Article  MATH  Google Scholar 

  19. Soleymani, F., Vanani, S.K., Khan, M., Sharifi, M.: An improvement of Ostrowski’s and King’s techniques with optimal convergence order eight. J. Optim. Theory Appl. 153, 225–236 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  20. Soleymani, F., Sharifi, M.: On a general efficient class of four-step root-finding methods. Int. J. Math. Comput. Simul. 5, 181–189 (2011)

    Google Scholar 

  21. Traub, J.F.: Iterative Methods for the Solution of Equations. Chelsea, New York (1982)

    MATH  Google Scholar 

  22. Ahlfors, L.V.: Complex Analysis. McGraw-Hill, New York (1979)

    MATH  Google Scholar 

  23. Wolfram, S.: The Mathematica Book, 5th edn. Wolfram Media, Champaign (2003)

    Google Scholar 

Download references

Acknowledgements

The corresponding author (Y.I. Kim) was supported by the Research Fund of Dankook University in 2012. In addition, the authors would like to give special thanks to anonymous referees for their valuable suggestions and comments as well as excellent english corrections on this paper.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Dankook University, Cheonan, 330-714, Korea

    Young Hee Geum & Young Ik Kim

Authors
  1. Young Hee Geum
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Young Ik Kim
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Young Ik Kim.

Additional information

Communicated by Ilio Galligani.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Geum, Y.H., Kim, Y.I. An Optimal Family of Fast 16th-Order Derivative-Free Multipoint Simple-Root Finders for Nonlinear Equations. J Optim Theory Appl 160, 608–622 (2014). https://doi.org/10.1007/s10957-013-0268-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-013-0268-x

Keywords