Abstract
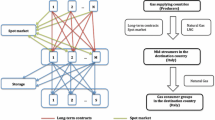
Liquefied Natural Gas contracts offer cancelation options that make their pricing difficult, especially if many gas storages need to be taken into account. We develop a valuation mechanism from the buyer’s perspective, a large gas company whose main interest in these contracts is to provide to clients a reliable supply of gas. The approach combines valuation with hedging, taking into account that price-risk is driven by international markets, while volume-risk depends on local weather and is stage-wise dependent. The methodology is based on setting risk-averse stochastic mixed 0-1 programs, for different contract configurations. These difficult problems are solved with light computational effort, thanks to a robust rolling-horizon approach. The resulting pricing mechanism not only shows how a specific set of contracts will impact the company business, but also provides the manager with alternative contract configurations to counter-propose to the contract seller.







Similar content being viewed by others
References
van der Vlerk, M.H.: Stochastic Programming with Integer Recourse. Labyrinth, Berkeley (1995)
Dentcheva, D., Ruszczyński, A., Shapiro, A.: Lectures on Stochastic Programming. SIAM, Philadelphia (2009)
Fodstad, A., Midthun, K., Romo, F., Tomasgard, A.: Optimization models for the natural gas value chain. In: Geometric Modeling, Numerical Simulation, and Optimization, pp. 521–558. SINTEF, Trondheim (2007)
Haurie, A., Smeers, Y., Zaccour, G.: Toward a contract portfolio management model for a gas producing firm. INFOR 30(3), 257–273 (1992)
Haurie, A., Smeers, Y., Zaccour, G.: Gas contract portfolio management: experiments with a stochastic programming approach. In: Lesourd, J.-B., Percebois, J., Valette, F. (eds.) Models for Energy Policy, pp. 521–558. Routledge, London (1996)
Allevi, E., Bertocchi, M., Vespucci, M., Innorta, M.: A mixed integer nonlinear optimization model for gas sale company. Optim. Lett. 1(1), 61–69 (2007)
Maggioni, F., Vespucci, M., Allevi, E., Bertocchi, M., Innorta, M.: A two-stage stochastic optimization model for a gas sale retailer. Kybernetika 44(2), 277–296 (2008)
Secomandi, N., Lai, G., Margot, F., Scheller-Wolf, A., Seppil, D.: The effect of model error on the valuation and hedging of natural gas storage. Tech. rep. Tepper, School of Business, Carnegie Mellon University (2010)
Dixit, A., Pindyck, R.: Investment Under Uncertainty. Princeton University Press, Princeton (1994)
Trigeorgis, L.: Real Options: Managerial Flexibility and Strategy in Resource Allocation. The MIT Press, Cambridge (1999)
Byers, J.W.: A two-stage stochastic optimization model for a gas sale retailer. Energy Econ. 28(3), 275–287 (2006)
Abadie, L.M., Chamorro, J.M.: Monte Carlo valuation of natural gas investments. Rev. Financ. Econ. 18(1), 10–22 (2009)
Lai, G., Margot, F., Secomandi, N.: An approximate dynamic programming approach to benchmark practice-based heuristics for natural gas storage valuation. Oper. Res. 58, 564–582 (2010)
Schwartz, E., Smith, J.E.: Short-term variations and long-term dynamics in commodity prices. Manag. Sci. 46(7), 893–911 (2000)
Cartea, A., Thomas, W.: UK markets: the market price of risk and applications to multiple interruptible supply contracts. Energy Econ. 30(3), 829–846 (2008)
Sørensen, C.: Modeling seasonality in agricultural commodity futures. J. Futures Mark. 22(5), 393–426 (2002)
Stoll, S.O., Wiebauer, K.: A spot price model for natural gas considering temperature as an exogenous factor with applications. J. Energy Mark. 3(3), 113–128 (2010)
Xu, J.: Stochastic models for gas prices. Master’s thesis, Department of Mathematics and Statistics, The University of Calgary, Canada (2004)
Kalman, R.E.: A new approach to linear filtering and prediction problems. J. Basic Eng. 82, 35–45 (1960)
Aiube, F.A.L., Baidya, T.K.N., Tito, E.A.H.: Analysis of commodity prices with the particle filter. Energy Econ. 30, 597–605 (2008)
Rockafellar, R.T., Uryasev, S.: Conditional value-at-risk for general loss distributions. J. Bank. Finance 26(7), 1443–1471 (2002)
Maceira, M.E., Damázio, J.: The use of PAR(p) model in the stochastic dual dynamic programming optimization scheme used in the operation planning of the Brazilian hydropower system. Probab. Methods Appl. Power Syst., 397–402 (2004)
Guigues, V., Sagastizábal, C.: Risk-averse feasible policies for stochastic linear programming. Math. Program., Ser. A 138(1–2), 167–198 (2013)
Ben-Tal, A., Nemirovski, A.: Robust convex optimization. Math. Oper. Res. 23(4), 769–805 (1998)
Guigues, V., Sagastizábal, C.: The value of rolling horizon policies for risk-averse hydro-thermal planning. Eur. J. Oper. Res. 217, 219–240 (2012)
Shapiro, A.: On a time consistency concept in risk averse multistage stochastic programming. Oper. Res. Lett. 37(3), 143–147 (2009)
Pereira, M., Pinto, L.: Multi-stage stochastic optimization applied to energy planning. Math. Program., Ser. A 52(2), 359–375 (1991)
Street, A., Barroso, L.A., Chabar, R., Mendes, A.T., Pereira, M.V.: Pricing flexible natural gas supply contracts under uncertainty in hydrothermal markets. IEEE Trans. Power Syst. 23, 1009–1017 (2008)
Acknowledgements
The authors are grateful to Steven Lillywhite for his implementation of the Schwartz and Smith model calibration.
CS was supported by CNPq grant 303840, PRONEX-Optimization, and FAPERJ. JPZ was supported by CNPq grants 302161 and 474085, and by the FAPERJ/CEST program.
Author information
Authors and Affiliations
Corresponding author
Additional information
C. Sagastizábal is a visiting researcher at IMPA, on leave from INRIA, France.
Rights and permissions
About this article
Cite this article
Guigues, V., Sagastizábal, C. & Zubelli, J.P. Robust Management and Pricing of Liquefied Natural Gas Contracts with Cancelation Options. J Optim Theory Appl 161, 179–198 (2014). https://doi.org/10.1007/s10957-013-0309-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-013-0309-5