Skip to main content
Springer Nature Link
Log in

Support Vector Machine Polyhedral Separability in Semisupervised Learning

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

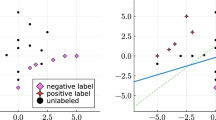
We introduce separation margin maximization, a characteristic of the Support Vector Machine technique, into the approach to binary classification based on polyhedral separability and we adopt a semisupervised classification framework.

In particular, our model aims at separating two finite and disjoint sets of points by means of a polyhedral surface in the semisupervised case, that is, by exploiting information coming from both labeled and unlabeled samples. Our formulation requires the minimization of a nonconvex nondifferentiable error function. Numerical results are presented on several data sets drawn from the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Megiddo, N.: On the complexity of polyhedral separability. Discrete Comput. Geom. 3, 325–337 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  2. Astorino, A., Gaudioso, M.: Polyhedral separability through successive LP. J. Optim. Theory Appl. 112(2), 265–293 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  3. Bagirov, A.M., Ugon, J., Webb, D., Ozturk, G., Kasimbeyli, R.: A novel piecewise linear classifier based on polyhedral conic and max-min separabilities. TOP 21(1), 3–24 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  4. Gasimov, R.N., Ozturk, G.: Separation via polyhedral conic functions. Optim. Methods Softw. 21(4), 527–540 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  5. Orsenigo, C., Vercellis, C.: Accurately learning from few examples with a polyhedral classifier. Comput. Optim. Appl. 38(2), 235–247 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  6. Cristianini, N., Shawe-Taylor, J.: An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge University Press, Cambridge (2000)

    Book  Google Scholar 

  7. Schölkopf, B., Burges, C.J.C., Smola, A.J.: Advances in Kernel Methods. Support Vector Learning. MIT Press, Cambridge (1999)

    Google Scholar 

  8. Schölkopf, B., Smola, A.J.: Learning with Kernels. MIT Press, Cambridge (2002)

    Google Scholar 

  9. Shawe-Taylor, J., Cristianini, N.: Kernel Methods for Pattern Analysis. Cambridge University Press, Cambridge (2004)

    Book  Google Scholar 

  10. Vapnik, V.: The Nature of the Statistical Learning Theory. Springer, New York (1995)

    Book  MATH  Google Scholar 

  11. Joachims, T.: Transductive inference for text classification using support vector machines. In: International Conference on Machine Learning, pp. 200–209 (1999)

    Google Scholar 

  12. Joachims, T.: Transductive learning via spectral graph partitioning. In: Proceedings of the International Conference on Machine Learning, pp. 290–297 (2003)

    Google Scholar 

  13. Astorino, A., Fuduli, A., Gorgone, E.: Non-smoothness in classification problems. Optim. Methods Softw. 23(5), 675–688 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  14. Chapelle, O., Schölkopf, B., Zien, A. (eds.): Semi-Supervised Learning. MIT Press, Cambridge (2006)

    Google Scholar 

  15. Bennett, K.P., Demiriz, A.: Semi-supervised support vector machines. In: Kearns, M.S., Solla, S.A., Cohn, D.A. (eds.) Advances in Neural Information Processing Systems, vol. 12, pp. 368–374. MIT Press, Cambridge (1998)

    Google Scholar 

  16. Fung, G., Mangasarian, O.L.: Semi-supervised support vector machines for unlabeled data classification. Optim. Methods Softw. 15, 29–44 (2001)

    Article  MATH  Google Scholar 

  17. Chapelle, O., Zien, A.: Semi-supervised classification by low density separation. In: Proceedings of the Tenth International Workshop on Artificial Intelligence and Statistics, pp. 57–64 (2005)

    Google Scholar 

  18. Astorino, A., Fuduli, A.: Nonsmooth optimization techniques for semisupervised classification. IEEE Trans. Pattern Anal. Mach. Intell. 29(12), 2135–2142 (2007)

    Article  Google Scholar 

  19. Chapelle, O., Sindhwani, V., Keerthi, S.S.: Branch and bound for semi-supervised support vector machines. In: Advances in Neural Information Processing Systems, pp. 217–224 (2007)

    Google Scholar 

  20. Bie, T., Cristianini, N.: Semi-supervised learning using semi-definite programming. In: Chapelle, O., Schölkopf, B., Zien, A. (eds.) Semi-Supervised Learning. MIT, Cambridge (2006)

    Google Scholar 

  21. Astorino, A., Gorgone, E., Gaudioso, M., Pallaschke, D.: Data preprocessing in semi-supervised SVM classification. Optimization 60(1–2), 143–151 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  22. Chapelle, O., Sindhwani, V., Keerthi, S.S.: Optimization techniques for semi-supervised support vector machines. J. Mach. Learn. Res. 9, 203–233 (2008)

    MATH  Google Scholar 

  23. Bagirov, A.M., Ugon, J., Webb, D., Karasözen, B.: Classification through incremental max-min separability. Pattern Anal. Appl. 14(2), 165–174 (2011)

    Article  MathSciNet  Google Scholar 

  24. Bagirov, A.M.: Max-min separability. Optim. Methods Softw. 20(2–3), 271–290 (2005)

    MathSciNet  Google Scholar 

  25. Astorino, A., Fuduli, A., Gaudioso, M.: DC models for spherical separation. J. Glob. Optim. 48(4), 657–669 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  26. Astorino, A., Fuduli, A., Gaudioso, M.: Margin maximization in spherical separation. Comput. Optim. Appl. 53(2), 301–322 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  27. Astorino, A., Gaudioso, M.: Ellipsoidal separation for classification problems. Optim. Methods Softw. 20(2–3), 261–270 (2005)

    MathSciNet  Google Scholar 

  28. Astorino, A., Gaudioso, M., Seeger, A.: Conic separation of finite sets. I. The homogeneous case. J. Convex Anal. 21(1) (2014)

  29. Le Thi, H.A., Le, H.M., Pham Dinh, T., Van Huynh, N.: Binary classification via spherical separator by DC programming and DCA. J. Glob. Optim. 56(4), 1393–1407 (2013)

    Article  MATH  Google Scholar 

  30. Chapelle, O., Vapnik, V., Bousquet, O., Mukherjee, S.: Choosing multiple parameters for support vector machines. Mach. Learn. 46(1–3), 131–159 (2002)

    Article  MATH  Google Scholar 

  31. Collobert, R., Sinz, F., Weston, J., Bottou, L.: Large scale transductive SVMs. J. Mach. Learn. Res. 7, 1687–1712 (2006)

    MATH  MathSciNet  Google Scholar 

  32. Fuduli, A., Gaudioso, M., Giallombardo, G.: Minimizing nonconvex nonsmooth functions via cutting planes and proximity control. SIAM J. Optim. 14(3), 743–756 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  33. Bergeron, C., Moore, G., Zaretzki, J., Breneman, C., Bennett, K.: Fast bundle algorithm for multiple instance learning. IEEE Trans. Pattern Anal. Mach. Intell. 34(6), 1068–1079 (2012)

    Article  Google Scholar 

  34. Hiriart-Urruty, J.B., Lemaréchal, C.: Convex Analysis and Minimization Algorithms, Vols. I–II. Springer, Berlin (1993)

    Google Scholar 

  35. Murphy, P.M., Aha, D.W.: UCI repository of machine learning databases. In (1992). www.ics.uci.edu/~mlearn/MLRepository.html

  36. Odewahn, S., Stockwell, E., Pennington, R., Humphreys, R., Zumach, W.: Automated star/galaxy discrimination with neural networks. Astron. J. 103(1), 318–331 (1992)

    Article  Google Scholar 

  37. Chang, C.C., Lin, C.J.: LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2, 27:1–27:27 (2011). Software available at www.csie.ntu.edu.tw/~cjlin/libsvm

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Istituto di Calcolo e Reti ad Alte Prestazioni-C.N.R. c/o D.E.I.S., Università della Calabria, 87036, Rende (CS), Italia

    Annabella Astorino

  2. Dipartimento di Matematica e Informatica, Università della Calabria, 87036, Rende (CS), Italia

    Antonio Fuduli

Authors
  1. Annabella Astorino
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Antonio Fuduli
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Annabella Astorino.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Astorino, A., Fuduli, A. Support Vector Machine Polyhedral Separability in Semisupervised Learning. J Optim Theory Appl 164, 1039–1050 (2015). https://doi.org/10.1007/s10957-013-0458-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-013-0458-6

Keywords