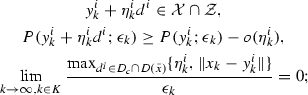Abstract
Methods which do not use any derivative information are becoming popular among researchers, since they allow to solve many real-world engineering problems. Such problems are frequently characterized by the presence of discrete variables, which can further complicate the optimization process. In this paper, we propose derivative-free algorithms for solving continuously differentiable Mixed Integer NonLinear Programming problems with general nonlinear constraints and explicit handling of bound constraints on the problem variables. We use an exterior penalty approach to handle the general nonlinear constraints and a local search approach to take into account the presence of discrete variables. We show that the proposed algorithms globally converge to points satisfying different necessary optimality conditions. We report a computational experience and a comparison with a well-known derivative-free optimization software package, i.e., NOMAD, on a set of test problems. Furthermore, we employ the proposed methods and NOMAD to solve a real problem concerning the optimal design of an industrial electric motor. This allows to show that the method converging to the better extended stationary points obtains the best solution also from an applicative point of view.



Similar content being viewed by others
Notes
Available for download at: http://www.dis.uniroma1.it/~lucidi/DFL.
References
Conn, A., Scheinberg, K., Vicente, L.: Introduction to Derivative-Free Optimization. MOS/SIAM Series on Optimization. SIAM, Philadelphia, MA (2009)
Abramson, M., Audet, C., Chrissis, J., Walston, J.: Mesh adaptive direct search algorithms for mixed variable optimization. Optim. Lett. 3(1), 35–47 (2009)
Audet, C., Dennis Jr, J.: Mesh adaptive direct search algorithms for constrained optimization. SIAM J. Optim. 17(1), 188–217 (2006)
Torczon, V.: On the convergence of pattern search algorithms. SIAM J. Optim. 7(1), 1–25 (1997)
Audet, C., Dennis Jr, J.: Analysis of generalized pattern searches. SIAM J. Optim. 13(3), 889–903 (2003)
Kolda, T., Lewis, R., Torczon, V.: Optimization by direct search: new perspectives on some classical and modern methods. SIAM Rev. 45(3), 385–482 (2003)
Audet, C., Dennis Jr, J.: Pattern search algorithms for mixed variable programming. SIAM J. Optim. 11(3), 573–594 (2001)
Kokkolaras, M., Audet, C., Dennis Jr, J.: Mixed variable optimization of the number and composition of heat intercepts in a thermal insulation system. Optim. Eng. 2(1), 5–29 (2001)
Abramson, M.: Pattern search filter algorithms for mixed variable general constrained optimization problems. Ph.D. thesis, Department of Computational and Applied Mathematics, Rice University (2002)
Abramson, M., Audet, C., Dennis Jr, J.: Filter pattern search algorithms for mixed variable constrained optimization problems. Pac. J. Optim. 3(3), 477–500 (2007)
Audet, C., Dennis Jr, J.: A pattern search filter method for nonlinear programming without derivatives. SIAM J. Optim. 14(4), 980–1010 (2004)
Vicente, L.: Implicitly and densely discrete black-box optimization problems. Optim. Lett. 3, 475–482 (2009)
Lucidi, S., Piccialli, V., Sciandrone, M.: An algorithm model for mixed variable programming. SIAM J. Optim. 14, 1057–1084 (2005)
Lucidi, S., Sciandrone, M., Tseng, P.: Objective-derivative-free methods for constrained optimization. Math. Program. 92(1), 37–59 (2002)
García-Palomares, U., Costa-Montenegro, E., Asorey-Cacheda, R., Gonzalez-Castano, F.J.: Adapting derivative free optimization methods to engineering models with discrete variables. Optim. Eng. 13, 579–594 (2012)
García-Palomares, U., Rodríguez, J.: New sequential and parallel derivative-free algorithms for unconstrained optimization. SIAM J. Optim. 13(1), 79–96 (2002)
Müller, J., Shoemaker, C., Piché, R.: So-mi: a surrogate model algorithm for computationally expensive nonlinear mixed-integer black-box global optimization problems. Comput. Oper. Res. 40(5), 1383–1400 (2013)
Laguna, M., Gortázar, F., Gallego, M., Duarte, A., Martí, R.: A black-box scatter search for optimization problems with integer variables. J. Glob. Optim. (2013). doi:10.1007/s10898-013-0061-2
Liuzzi, G., Lucidi, S., Rinaldi, F.: Derivative-free methods for bound constrained mixed-integer optimization. Comput. Optim. Appl. 53, 505–526 (2012)
Liuzzi, G., Lucidi, S., Sciandrone, M.: Sequential penalty derivative-free methods for nonlinear constrained optimization. SIAM J. Optim. 20, 2814–2835 (2010)
Lucidi, S., Sciandrone, M.: A derivative-free algorithm for bound constrained optimization. Comput. Optim. Appl. 21(2), 119–142 (2002)
Vicente, L.: Worst case complexity of direct search. EURO J. Comput. Optim. 1, 143–153 (2013)
Nesterov, Y.: Introductory Lectures on Convex Optimization. Kluwer Academic Publishers, Dordrecht (2004)
Lin, C.J., Lucidi, S., Palagi, L., Risi, A., Sciandrone, M.: A decomposition algorithm model for singly linearly constrained problems subject to lower and upper bounds. J. Optim. Theory Appl. 141, 107–126 (2009)
Bertsekas, D.: Nonlinear Programming, 2nd edn. Athena Scientific, Belmont, MA (1999)
Le Digabel, S.: Algorithm 909: Nomad: nonlinear optimization with the mads algorithm. ACM Trans. Math. Softw. 37(4), 1–15 (2011)
Hock, W., Schittkowski, K.: Test Examples for Nonlinear Programming Codes. Lecture notes in Economics and Mathematical Systems. Springer, Berlin (1981)
Hock, W., Schittkowski, K.: More Test Examples for Nonlinear Programming Codes. Lecture notes in Economics and Mathematical Systems. Springer, Berlin (1987)
Moré, J., Wild, S.: Benchmarking derivative-free optimization algorithms. SIAM J. Optim. 20(1), 172–191 (2009)
Lucidi, S., Parasiliti, F., Rinaldi, F., Villani, M.: Finite element based multi-objective design optimization procedure of interior permanent magnet synchronous motors for wide constant-power region operation. IEEE Trans. Ind. Electron. 59(6), 2503–2514 (2012)
Acknowledgments
We are indebted to two anonymous Reviewers whose many interesting suggestions and stimulating comments greatly helped us improving the paper. We thank Professors Franco Parasiliti and Marco Villani for providing us the optimal design problem and for giving useful insights and comments on the obtained results. Finally, we would like to mention that this work has been partially funded by the UE (ENIAC Joint Undertaking) in the MODERN project (ENIAC-120003).
Author information
Authors and Affiliations
Corresponding author
Appendix: Technical Result
Appendix: Technical Result
In this section, we report a technical result which is needed to prove convergence of DFL and EDFL. It is a slight modification of an analogous result reported in [20], which takes into account the presence of discrete variables.
Proposition 7.1
Let \(\{\epsilon _k\}\) be a bounded sequence of positive penalty parameters. Let \(\{x_k\}\) be a sequence of points such that \(x_k\in \mathcal{X}\cap \mathcal Z\) for all \(k\), and let \(\bar{x}\in \mathcal{X}\cap \mathcal Z\) be a limit point of a subsequence \(\{x_k\}_K\) for some infinite set \(K\subseteq \{0,1,\ldots \}\). Suppose that for each \(k\in K\) sufficiently large,
-
(i)
for all \(d^i\in D^c\cap D(\bar{x})\), there exist vectors \(y_k^i\) and scalars \(\eta _k^i>0\) such that
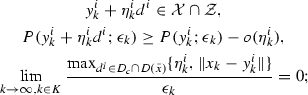
-
(ii)
$$\begin{aligned} \lim _{k\rightarrow \infty ,k\in K}\epsilon _k\Vert g^+(x_k)\Vert = 0; \end{aligned}$$
-
(iii)
$$\begin{aligned} (y_k^{i})_z = (x_k)_z,\qquad \text{ for } \text{ all }\ i\in I_c. \end{aligned}$$
Then, \(\bar{x}\) is a stationary point for Problem (1) with respect to the continuous variables, that is, \(\bar{x}\) satisfies (2) and (4) with \(\bar{\lambda }\in \mathbb {R}^m\) given by
where \(\lambda _j(x;\epsilon )\), \(j=1,\ldots ,m\), are defined in (8).
Proof
Considering point (iii), namely that the discrete variables are held fixed in the considered subsequence, the proof is the same as that of Proposition 3.1 in [20]. \(\square \)
Rights and permissions
About this article
Cite this article
Liuzzi, G., Lucidi, S. & Rinaldi, F. Derivative-Free Methods for Mixed-Integer Constrained Optimization Problems. J Optim Theory Appl 164, 933–965 (2015). https://doi.org/10.1007/s10957-014-0617-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-014-0617-4