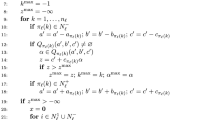Abstract
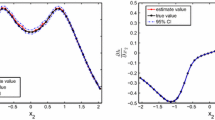
We deal with chance constrained problems with differentiable nonlinear random functions and discrete distribution. We allow nonconvex functions both in the constraints and in the objective. We reformulate the problem as a mixed-integer nonlinear program and relax the integer variables into continuous ones. We approach the relaxed problem as a mathematical problem with complementarity constraints and regularize it by enlarging the set of feasible solutions. For all considered problems, we derive necessary optimality conditions based on Fréchet objects corresponding to strong stationarity. We discuss relations between stationary points and minima. We propose two iterative algorithms for finding a stationary point of the original problem. The first is based on the relaxed reformulation, while the second one employs its regularized version. Under validity of a constraint qualification, we show that the stationary points of the regularized problem converge to a stationary point of the relaxed reformulation and under additional condition it is even a stationary point of the original problem. We conclude the paper by a numerical example.



Similar content being viewed by others
References
Charnes, A., Cooper, W.W., Symonds, G.H.: Cost horizons and certainty equivalents: an approach to stochastic programming of heating oil. Manag. Sci. 4(3), 235–263 (1958)
Rockafellar, R., Uryasev, S.: Conditional value-at-risk for general loss distributions. J. Bank. Finance 26(7), 1443–1471 (2002)
Wozabal, D., Hochreiter, R., Pflug, G.C.: A difference of convex formulation of value-at-risk constrained optimization. Optimization 59(3), 377–400 (2010)
van Ackooij, W., Henrion, R., Möller, A., Zorgati, R.: Joint chance constrained programming for hydro reservoir management. Optim. Eng. 15(2), 509–531 (2014)
Ehmke, J.F., Campbell, A.M., Urban, T.L.: Ensuring service levels in routing problems with time windows and stochastic travel times. Eur. J. Oper. Res. 240(2), 539–550 (2015)
van Ackooij, W., Sagastizábal, C.: Constrained bundle methods for upper inexact oracles with application to joint chance constrained energy problems. SIAM J. Optim. 24(2), 733–765 (2014)
Branda, M.: Optimization approaches to multiplicative tariff of rates estimation in non-life insurance. Asia Pac J. Oper. Res. 31(05), 1450,032 (2014)
Klein Haneveld, W., Streutker, M., van der Vlerk, M.: An ALM model for pension funds using integrated chance constraints. Ann. Oper. Res. 177(1), 47–62 (2010)
Luedtke, J., Ahmed, S.: A sample approximation approach for optimization with probabilistic constraints. SIAM J. Optim. 19(2), 674–699 (2008)
Beraldi, P., Bruni, M.: An exact approach for solving integer problems under probabilistic constraints with random technology matrix. Ann. Oper. Res. 177(1), 127–137 (2010)
Luedtke, J., Ahmed, S., Nemhauser, G.: An integer programming approach for linear programs with probabilistic constraints. Math. Program. 122(2), 247–272 (2010)
Prékopa, A.: Dual method for the solution of a one-stage stochastic programming problem with random RHS obeying a discrete probability distribution. Zeitschrift für Oper. Res. 34(6), 441–461 (1990)
Van Ackooij, W., Berge, V., De Oliveira, W., Sagastizabal, C.: Probabilistic optimization via approximate p-efficient points and bundle methods. Working Paper (2014)
Shapiro, A., Dentcheva, D., Ruszczyński, A.: Lectures on Stochastic Programming. Society for Industrial and Applied Mathematics, Philadelphia (2009)
Kogan, A., Lejeune, M.: Threshold boolean form for joint probabilistic constraints with random technology matrix. Math. Program. 147(1–2), 391–427 (2014)
Lejeune, M.A.: Pattern-based modeling and solution of probabilistically constrained optimization problems. Oper. Res. 60(6), 1356–1372 (2012)
Lejeune, M.A., Margot, F.: Solving chance-constrained optimization problems with stochastic quadratic inequalities. Tepper Working Paper E8 (2014)
Prékopa, A.: Probabilistic programming. In: Ruszczyński, A., Shapiro, A. (eds.) Stochastic Programming, Handbooks in Operations Research and Management Science, vol. 10, pp. 267–351. Elsevier, Amsterdam (2003)
Dentcheva, D., Martinez, G.: Augmented Lagrangian method for probabilistic optimization. Ann. Oper. Res. 200(1), 109–130 (2012)
Sun, H., Xu, H., Wang, Y.: Asymptotic analysis of sample average approximation for stochastic optimization problems with joint chance constraints via conditional value at risk and difference of convex functions. J. Optim. Theory Appl. 161(1), 257–284 (2014)
Haneveld, W., van der Vlerk, M.: Integrated chance constraints: reduced forms and an algorithm. Comput. Manag. Sci. 3(4), 245–269 (2006)
Nemirovski, A., Shapiro, A.: Convex approximations of chance constrained programs. SIAM J. Optim. 17(4), 969–996 (2007)
Hong, L.J., Yang, Y., Zhang, L.: Sequential convex approximations to joint chance constrained programs: A Monte Carlo approach. Oper. Res. 59(3), 617–630 (2011)
Cheng, J., Houda, M., Lisser, A.: Chance constrained 0–1 quadratic programs using copulas. Optim. Lett. 9(7), 1283–1295 (2015)
Henrion, R., Möller, A.: A gradient formula for linear chance constraints under Gaussian distribution. Math. Oper. Res. 37(3), 475–488 (2012)
Raike, W.M.: Dissection methods for solutions in chance constrained programming problems under discrete distributions. Manag. Sci. 16(11), 708–715 (1970)
Rockafellar, R.T., Wets, R.J.B.: Variational Analysis. Springer, Berlin (1998)
Flegel, M.L., Kanzow, C.: On the Guignard constraint qualification for mathematical programs with equilibrium constraints. Optimization 54(6), 517–534 (2005)
Burdakov, O., Kanzow, C., Schwartz, A.: On a reformulation of mathematical programs with cardinality constraints. In: Gao, D., Ruan, N., Xing, W. (eds.) Advances in Global Optimization, Springer Proceedings in Mathematics & Statistics, vol. 95, pp. 3–14. Springer International Publishing, Berlin (2015)
Červinka, M., Kanzow, C., Schwartz, A.: Constraint qualifications and optimality conditions for optimization problems with cardinality constraints. Math. Program. (2016). doi:10.1007/s10107-016-0986-6
Scholtes, S.: Convergence properties of a regularization scheme for mathematical programs with complementarity constraints. SIAM J. Optim. 11(4), 918–936 (2001)
Bonami, P., Lodi, A., Tramontani, A., Wiese, S.: On mathematical programming with indicator constraints. Math. Program. 151(1), 191–223 (2015)
Shan, F., Zhang, L., Xiao, X.: A smoothing function approach to joint chance-constrained programs. J. Optim. Theory Appl. 163(1), 181–199 (2014)
Ioffe, A.D., Outrata, J.: On metric and calmness qualification conditions in subdifferential calculus. Set Valued Anal. 16(2–3), 199–227 (2008)
Acknowledgments
The authors gratefully acknowledge the support from the Grant Agency of the Czech Republic under Project 15-00735S.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by René Henrion.
Appendix
Appendix
Together with the index sets defined in (6), we work with the following ones
Lemma 6.1
Denote Z to be the feasible set of problem (5), fix any \((\bar{x}, \bar{y})\in Z\) with \(\bar{y}\in Y(\bar{x})\). Let Assumption 2.1 be fulfilled at \(\bar{x}\). Then we have \(\hat{N}_Z(\bar{x},\bar{y})=N_1(\bar{x})\times N_2(\bar{y}),\) where
Proof
For \(I\subset I_{00}(\bar{x},\bar{y})\) define sets
and observe that union of \(Z_I:=Z_I^x\times Z_I^y\) with respect to all \(I\subset I_{00}(\bar{x},\bar{y})\) locally around \((\bar{x},\bar{y})\) coincides with Z, which implies
This means that we have
The lemma statement them follows from [34, Proposition 3.4] and [27, Theorem 6.14]. \(\square \)
Rights and permissions
About this article
Cite this article
Adam, L., Branda, M. Nonlinear Chance Constrained Problems: Optimality Conditions, Regularization and Solvers. J Optim Theory Appl 170, 419–436 (2016). https://doi.org/10.1007/s10957-016-0943-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-016-0943-9