Skip to main content

Advertisement

Springer Nature Link
Log in

Data-Driven Robust Chance Constrained Problems: A Mixture Model Approach

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

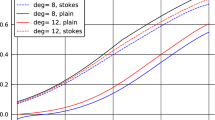
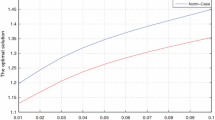
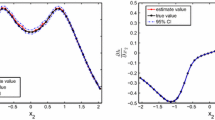
This paper discusses the mixture distribution-based data-driven robust chance constrained problem. We construct a data-driven mixture distribution-based uncertainty set from the perspective of simultaneously estimating higher-order moments. Then, we derive a reformulation of the data-driven robust chance constrained problem. As the reformulation is not a convex programming problem, we propose new and tight convex approximations based on the piecewise linear approximation method. We establish the theoretical foundation for these approximations. Finally, numerical results show that the proposed approximations are practical and efficient.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Charnes, A., Cooper, W.W.: Chance-constrained programming. Manage. Sci. 6(1), 73–79 (1959)

    Article  MathSciNet  Google Scholar 

  2. Miller, B.L., Wagner, H.M.: Chance constrained programming with joint constraints. Oper. Res. 13(6), 930–945 (1965)

    Article  Google Scholar 

  3. Calafiore, G., Dabbene, F.: Probabilistic and Randomized Methods for Design under Uncertainty. Springer, London (2006)

    Book  Google Scholar 

  4. Prékopa, A.: Stochastic Programming. Springer, Dordrecht (1995)

    Book  Google Scholar 

  5. Shapiro, A., Dentcheva, D., Ruszczynski, A.: Lectures on Stochastic Programming: Modeling and Theory. SIAM, Philadelphia (2009)

    Book  Google Scholar 

  6. Prékopa, A.: Logarithmic concave measures with application to stochastic programming. Acta Sci. Math. 32(3–4), 301–316 (1971)

    MathSciNet  MATH  Google Scholar 

  7. Jagannathan, R.: Chance-constrained programming with joint constraints. Oper. Res. 22(2), 358–372 (1974)

    Article  MathSciNet  Google Scholar 

  8. Luedtke, J., Ahmed, S., Nemhauser, G.L.: An integer programming approach for linear programs with probabilistic constraints. Math. Program. 122(2), 247–272 (2010)

    Article  MathSciNet  Google Scholar 

  9. Nemirovski, A., Shapiro, A.: Scenario approximations of chance constraints. In: Calafiore, G., Dabbene, F. (eds.) Probabilistic and Randomized Methods for Design under Uncertainty, pp. 3–47. Springer, London (2006)

    Chapter  Google Scholar 

  10. Ben-Tal, A., Nemirovski, A.: Robust solutions of linear programming problems contaminated with uncertain data. Math. Program. 88(3), 411–424 (2000)

    Article  MathSciNet  Google Scholar 

  11. Nemirovski, A., Shapiro, A.: Convex approximations of chance constrained programs. SIAM J. Optim. 17(4), 969–996 (2006)

    Article  MathSciNet  Google Scholar 

  12. Zymler, S., Kuhn, D., Rustem, B.: Distributionally robust joint chance constraints with second-order moment information. Math. Program. 137(1), 167–198 (2013)

    Article  MathSciNet  Google Scholar 

  13. Calafiore, G.C., El Ghaoui, L.: On distributionally robust chance-constrained linear programs. J. Optim. Theory Appl. 130(1), 1–22 (2006)

    Article  MathSciNet  Google Scholar 

  14. Erdogan, E., Iyengar, G.: Ambiguous chance constrained problems and robust optimization. Math. Program. 107(1), 37–61 (2006)

    Article  MathSciNet  Google Scholar 

  15. Li, B., Jiang, R., Mathieu, J.L.: Ambiguous risk constraints with moment and unimodality information. Math. Program. (2017). https://doi.org/10.1007/s10107-017-1212-x

  16. Delage, E., Ye, Y.: Distributionally robust optimization under moment uncertainty with application to data-driven problems. Oper. Res. 58(3), 595–612 (2010)

    Article  MathSciNet  Google Scholar 

  17. Cheng, J., Delage, E., Lisser, A.: Distributionally robust stochastic knapsack problem. SIAM J. Optim. 24(3), 1485–1506 (2014)

    Article  MathSciNet  Google Scholar 

  18. Hanasusanto, G.A., Roitch, V., Kuhn, D., Wiesemann, W.: Ambiguous joint chance constraints under mean and dispersion information. Oper. Res. 65(3), 751–767 (2017)

    Article  MathSciNet  Google Scholar 

  19. Bertsimas, D., Gupta, V., Kallus, N.: Data-driven robust optimization. Math. Program. 167, 235–292 (2018)

    Article  MathSciNet  Google Scholar 

  20. Zhu, S., Fan, M., Li, D.: Portfolio management with robustness in both prediction and decision: a mixture model based learning approach. J. Econ. Dyn. Control 48(C), 1–25 (2014)

    Article  MathSciNet  Google Scholar 

  21. Duffie, D., Pan, J.: An overview of value at risk. J. Deriv. 4(3), 7–49 (1997)

    Article  Google Scholar 

  22. McNeil, A.J., Frey, R., Embrechts, P.: Quantitative Risk Management: Concepts, Techniques and Tools. Princeton University Press, Princeton (2005)

    MATH  Google Scholar 

  23. Hall, J.A., Brorsen, W., Irwin, S.H.: The distribution of futures prices: a test of the stable paretian and mixture of normals hypotheses. J. Financ. Quant. Anal. 24(1), 105–116 (1989)

    Article  Google Scholar 

  24. Peel, D., McLachlan, G.J.: Robust mixture modeling using the \(t\) distribution. Stat. Comput. 10(4), 339–348 (2000)

    Article  Google Scholar 

  25. Zhu, S., Fukushima, M.: Worst-case conditional value-at-risk with application to robust portfolio management. Oper. Res. 57(5), 1155–1168 (2009)

    Article  MathSciNet  Google Scholar 

  26. Gupta, V.: Near-optimal ambiguity sets for distributionally robust optimization. http://www.optimization-online.org/DB_FILE/2015/07/4983.pdf (2015). Accessed 7 Jan 2015

  27. Eisenberger, I.: Genesis of bimodal distributions. Technometrics 6(4), 357–363 (1964)

    Article  MathSciNet  Google Scholar 

  28. Ray, S., Lindsay, B.G.: The topography of multivariate normal mixtures. Ann. Stat. 33(5), 2042–2065 (2005)

    Article  MathSciNet  Google Scholar 

  29. Mccauley, J.L.: Dynamics of Markets: The New Financial Economics. Cambridge University Press, New York (2009)

    Book  Google Scholar 

  30. Habib, M., McDiarmid, C., Ramirez-Alfonsin, J., Reed, B.: Probabilistic Methods for Algorithmic Discrete Mathematics. Springer, Berlin (1998)

    Book  Google Scholar 

  31. van der Vaart, A.W., Wellner, J.A.: Weak Convergence and Empirical Processes: With Applications to Statistics, 2nd edn. Springer, New York (1996)

    Book  Google Scholar 

  32. Calafiore, G.C., Campi, M.C.: The scenario approach to robust control design. IEEE Trans. Automat. Contr. 51(5), 742–753 (2006)

    Article  MathSciNet  Google Scholar 

  33. Ben-Tal, A., El Ghaoui, L., Nemirovski, A.: Robust Optimization. Princeton University Press, Princeton (2009)

    Book  Google Scholar 

  34. Liu, J., Lisser, A., Chen, Z.: Stochastic geometric optimization with joint probabilistic constraints. Oper. Res. Lett. 44(5), 687–691 (2016)

    Article  MathSciNet  Google Scholar 

  35. Rockafellar, R.T., Wets, R.J.B.: Variational Analysis. Springer, Berlin (1998)

    Book  Google Scholar 

  36. Eaves, B.C.: Finite solution of pure trade markets with Cobb–Douglas utilities. In: Manne, A.S. (ed.) Economic Equilibrium: Model Formulation and Solution, Mathematical Programming Studies, vol. 23, pp. 226–239. Springer, Berlin (1985)

    Chapter  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the relevant editors and two anonymous reviewers for their extremely detailed and insightful comments and suggestions, which have led to a substantial improvement of the paper in both content and style. This research was supported by the National Natural Science Foundation of China (Grant Nos. 11571270 and 71371152 ).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an, Shaanxi, 710049, People’s Republic of China

    Zhiping Chen, Shen Peng & Jia Liu

Authors
  1. Zhiping Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Shen Peng
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jia Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zhiping Chen.

Additional information

Communicated by Evgeni A. Nurminski.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, Z., Peng, S. & Liu, J. Data-Driven Robust Chance Constrained Problems: A Mixture Model Approach. J Optim Theory Appl 179, 1065–1085 (2018). https://doi.org/10.1007/s10957-018-1376-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-018-1376-4

Keywords

Mathematics Subject Classification

Profiles

  1. Jia Liu View author profile