Skip to main content

Advertisement

Springer Nature Link
Log in

On Stochastic Extremum Seeking via Adaptive Perturbation–Demodulation Loop

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

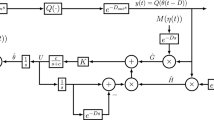
In this paper, we propose a stochastic approximation algorithm for optimization of functions based on an adaptive extremum seeking method. The essence of this method is to approximate the gradient direction by introduction of a probing sequence, that is added to approximations and subsequently demodulated using an adaptive gain. Assuming that the probing and the demodulation signals are martingale difference sequences with adaptive diminishing gains, it is proved that the approximations converge almost surely to the optimizing value, under mild constraints on the measurement disturbance, and without assuming a priori boundedness of the approximation sequence. The measurement disturbance can contain a stochastic component, as well as a mean-square bounded deterministic component. The stochastic component can be nonstationary colored noise or a state-dependent random sequence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Tan, Y., Moase, W., Manzie, C., Nešić, D., Mareels, I.: Extremum seeking from 1922 to 2010. In: Proceedings of 29th Chinese Control Conference, pp. 14–26 (2010)

  2. Choi, J.Y., Krstić, M., Ariyur, K.B., Lee, J.S.: Extremum seeking control for discrete-time systems. IEEE Trans. Autom. Control 47, 318–323 (2002)

    Article  MathSciNet  Google Scholar 

  3. Ghaffari, A., Krstić, M., Nešić, D.: Multivariable Newton-based extremum seeking. Automatica 48, 1759–1767 (2012)

    Article  MathSciNet  Google Scholar 

  4. Stanković, M.S., Stipanović, D.M.: Extremum seeking under stochastic noise and applications to mobile sensors. Automatica 46, 1243–1251 (2010)

    Article  MathSciNet  Google Scholar 

  5. Manzie, C., Krstić, M.: Extremum seeking with stochastic perturbations. IEEE Trans. Autom. Control 54, 580–585 (2009)

    Article  MathSciNet  Google Scholar 

  6. Liu, S.J., Krstić, M.: Stochastic averaging in discrete time and its applications to extremum seeking. IEEE Trans. Autom. Control 61, 90–102 (2015)

    Article  MathSciNet  Google Scholar 

  7. Radenković, M.S., Altman, T.: Stochastic adaptive stabilization via extremum seeking in case of unknown control directions. IEEE Trans. Autom. Control 61(11), 3681–3686 (2016)

    Article  MathSciNet  Google Scholar 

  8. Kiefer, J., Wolfowitz, J.: Stochastic estimation of the maximum of a regression function. Ann. Math. Stat. 23(3), 462–466 (1952)

    Article  MathSciNet  Google Scholar 

  9. Kushner, H.J., Clark, D.S.: Stochastic Approximation Methods for Constrained and Unconstrained Systems. Applied Mathematical Sciences, vol. 26. Springer, Berlin (1978)

    Book  Google Scholar 

  10. Chin, D.C.: Comparative study of stochastic algorithms for system optimization based on gradient approximations. IEEE Trans. Syst. Man Cybern. Part B Cybern. 27(2), 244–249 (1997)

    Article  Google Scholar 

  11. Spall, J.C.: Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Trans. Autom. Control 37, 332–341 (1992)

    Article  MathSciNet  Google Scholar 

  12. Spall, J.C.: A one-measurement form of simultaneous perturbation stochastic approximation. Automatica 33, 109–112 (1997)

    Article  MathSciNet  Google Scholar 

  13. Dvoretsky, A.: On stochastic approximation. In: Proceedings of 3rd Berkeley Symposium on Mathematical Statistics and Probability, vol. 1, pp. 39–56 (1956)

  14. Nevelson, M.B., Hasminsky, R.Z.: Stochastic Approximation and Recursive Estimation. AMS Providence, Rhode Island (1973)

    Google Scholar 

  15. Wada, T., Fujisaki, Y.: Stopping rules for optimization algorithms based on stochastic approximation. J. Optim. Theory Appl. 169(2), 568–586 (2016)

    Article  MathSciNet  Google Scholar 

  16. Granichin, O.N.: Randomized algorithms for stochastic approximation under arbitrary disturbances. Autom. Remote Control 63(2), 209–219 (2002)

    Article  MathSciNet  Google Scholar 

  17. Lai, T.L., Wei, C.Z.: Least square estimates in stochastic regression models with applications to identification and control of dynamic systems. Ann. Stat. 10, 154–166 (1982)

    Article  MathSciNet  Google Scholar 

  18. Spall, J.C.: Adaptive stochastic approximation by the simultaneous perturbation method. IEEE Trans. Autom. Control 45, 1839–1853 (2000)

    Article  MathSciNet  Google Scholar 

  19. Prashanth, L., Bhatnagar, S., Fu, M., Marcus, S.: Adaptive system optimization using random directions stochastic approximation. IEEE Trans. Autom. Control 62(5), 2223–2238 (2017)

    Article  MathSciNet  Google Scholar 

  20. Kumar, P.R., Varaiya, P.: Stochastic Systems: Estimation, Identification and Adaptive Control. Prentice-Hall, Inc., Upper Saddle River (1986)

    MATH  Google Scholar 

Download references

Acknowledgements

Funding of the author Miloš S. Stanković was provided by Seventh Framework Programme (Grant No. PCIG12-GA-2012-334098).

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, University of Colorado Denver, Denver, CO, 80217-3364, USA

    Miloje S. Radenković

  2. Innovation Center, School of Electrical Engineering, University of Belgrade, Belgrade, Serbia

    Miloš S. Stanković

  3. School of Technical Sciences, Singidunum University, Belgrade, Serbia

    Miloš S. Stanković

  4. Vlatacom Institute, Belgrade, Serbia

    Miloš S. Stanković & Srdjan S. Stanković

  5. School of Electrical Engineering, University of Belgrade, Belgrade, Serbia

    Srdjan S. Stanković

Authors
  1. Miloje S. Radenković
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Miloš S. Stanković
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Srdjan S. Stanković
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Miloš S. Stanković.

Additional information

Communicated by Jyh-Horng Chou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Radenković, M.S., Stanković, M.S. & Stanković, S.S. On Stochastic Extremum Seeking via Adaptive Perturbation–Demodulation Loop. J Optim Theory Appl 179, 1008–1024 (2018). https://doi.org/10.1007/s10957-018-1380-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-018-1380-8

Keywords