Skip to main content
Springer Nature Link
Log in

An Extragradient Method for Solving Variational Inequalities without Monotonicity

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

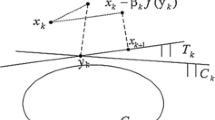
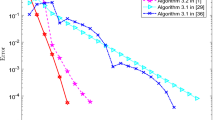
A new extragradient projection method, which does not require generalized monotonicity, is devised in this paper. In order to ensure its global convergence, we assume only that the Minty variational inequality has a solution. In particular, it applies to quasimonotone variational inequalities having a nontrivial solution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Goldstein, A.A.: Convex programming in Hilbert space. Bull. Am. Math. Soc. 70, 709–710 (1964)

    Article  MathSciNet  Google Scholar 

  2. Levitin, E.S., Polyak, B.T.: Constrained minimization problems. USSR Comput. Math. Math. Phys. 6, 1–50 (1966)

    Article  Google Scholar 

  3. Konnov, I.V.: Combined relaxation methods for finding equilibrium points and solving related problems. Russ. Math. (Iz VUZ) 37, 44–51 (1993)

    MATH  Google Scholar 

  4. Konnov, I. V.: Combined relaxation methods for generalized monotone variational inequalities. Generalized Convexity and Related Topics. Lecture Notes in Economics and Mathematical systems, pp. 3-31. Springer Berlin Heidelberg, Heidelberg (2006)

  5. Konnov, I.V.: Combined Relaxation Methods for Variational Inequalities. Springer-Verlag, Berlin (2001)

    Book  Google Scholar 

  6. Korpelevich, G.M.: The extragradient method for finding saddle points and other problems. Matecon. 17, 747–756 (1976)

    MathSciNet  MATH  Google Scholar 

  7. Iusem, A.N.: An iterative algorithm for the variational inequality problem. Math. Appl. Comput. 13, 103–114 (1994)

    MathSciNet  MATH  Google Scholar 

  8. Iusem, A.N., Svaiter, B.F.: A variant of Korpelevich’s method for variational inequalities with a new search strategy. Optimization. 42, 309–321 (1997)

    Article  MathSciNet  Google Scholar 

  9. Wang, Y.J., Xiu, N.H., Wang, C.Y.: Unified framework of extragradient-type methods for pseudomonotone variational inequalities. J. Optim. Theory Appl. 111, 641–656 (2001)

    Article  MathSciNet  Google Scholar 

  10. Strodiot, J.J., Nguyen, T.T.V., Nguyen, V.H.: A new class of hybrid extragradient algorithms for solving quasi-equilibrium problems. J. Global Optim. 56, 373–397 (2013)

    Article  MathSciNet  Google Scholar 

  11. Hieu, D.V., Thong, D.V.: New extragradient-like algorithms for strongly pseudomonotone variational inequalities. J. Global Optim. 70, 385–399 (2018)

    Article  MathSciNet  Google Scholar 

  12. Vuong, P.T.: On the weak convergence of the extragradient method for solving pseudomonotone variational inequalities. J. Optim. Theory Appl. 176, 399–409 (2018)

    Article  MathSciNet  Google Scholar 

  13. Thong, D.V., Hieu, D.V.: Inertial extragradient algorithms for strongly pseudomonotone variational inequalities. J. Comput. Appl. Math. 341, 80–98 (2018)

    Article  MathSciNet  Google Scholar 

  14. Solodov, M.V., Svaiter, B.F.: A new projection method for variational inequality problems. SIAM J. Control Optim. 37, 765–776 (1999)

    Article  MathSciNet  Google Scholar 

  15. He, Y.R.: A new double projection algorithm for variational inequalities. J. Comput. Appl. Math. 185, 166–173 (2006)

    Article  MathSciNet  Google Scholar 

  16. Ye, M., He, Y.: A double projection method for solving variational inequalities without monotonicity. Comput. Optim. Appl. 60, 140–150 (2015)

    Article  MathSciNet  Google Scholar 

  17. Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 14, 877–898 (1976)

    Article  MathSciNet  Google Scholar 

  18. Facchinei, F., Pang, J.S.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer-Verlag, New York (2003)

    MATH  Google Scholar 

  19. Giannessi, F.: On Minty variational principle. In: Giannessi, F., Komlósi, S., Rapcsák, T. (eds.) New Trends in Mathematical Programming, pp. 93–99. Kluwer Academic Publishers, Dordrecht (1998)

    Chapter  Google Scholar 

  20. Hadjisavvas, N., Schaible, S.: Quasimonotone variational inequalities in Banach spaces. J. Optim. Theory Appl. 90, 95–111 (1996)

    Article  MathSciNet  Google Scholar 

  21. Xiu, N.H., Wang, C.Y.: On the step-size rule of extragradient method for monotone variational inequalities. Math. Numerica Sinica. 22, 197–208 (2000)

    MathSciNet  Google Scholar 

  22. Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (1970)

    Book  Google Scholar 

  23. Hiriart-Urruty, J.B., Lemaréchal, C.: Convex Analysis and Minimization Algorithms. Springer-Verlag, Berlin (1993)

    Book  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the referees for valuable suggestions. This work was partially supported by National Natural Science Foundation of China under Grant 11871359.

Author information

Authors and Affiliations

  1. Department of Mathematics, Sichuan Normal University, Chengdu, Sichuan, China

    Ming Lei & Yiran He

Authors
  1. Ming Lei
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yiran He
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yiran He.

Additional information

Communicated by Evgeni Alekseevich Nurminski.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lei, M., He, Y. An Extragradient Method for Solving Variational Inequalities without Monotonicity. J Optim Theory Appl 188, 432–446 (2021). https://doi.org/10.1007/s10957-020-01791-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-020-01791-x

Keywords

Mathematics Subject Classification