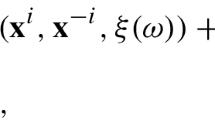Skip to main content
Springer Nature Link
Log in

A Proximal/Gradient Approach for Computing the Nash Equilibrium in Controllable Markov Games

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

This paper proposes a new algorithm for computing the Nash equilibrium based on an iterative approach of both the proximal and the gradient method for homogeneous, finite, ergodic and controllable Markov chains. We conceptualize the problem as a poly-linear programming problem. Then, we regularize the poly-linear functional employing a regularization approach over the Lagrange functional for ensuring the method to converge to some of the Nash equilibria of the game. This paper presents two main contributions: The first theoretical result is the proposed iterative approach, which employs both the proximal and the gradient method for computing the Nash equilibria in Markov games. The method transforms the game theory problem in a system of equations, in which each equation itself is an independent optimization problem for which the necessary condition of a minimum is computed employing a nonlinear programming solver. The iterated approach provides a quick rate of convergence to the Nash equilibrium point. The second computational contribution focuses on the analysis of the convergence of the proposed method and computes the rate of convergence of the step-size parameter. These results are interesting within the context of computational and algorithmic game theory. A numerical example illustrates the proposed approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. Utopia point can be used as an ideal standard for the criteria values to find the best solution(s) from the Pareto optimal set (see [22,23,24]).

References

  1. Nash, J.F.: Equilibrium points in n-person games. In: Proc. of the National Academy of Sciences, vol. 36, pp. 48–49 (1950)

  2. Facchinei, F., Pang, J.S.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer, New York (2003)

    MATH  Google Scholar 

  3. Nabetani, K., Tseng, P., Fukushima, M.: Parametrized variational inequality approaches to generalized Nash equilibrium problems with shared constraints. Comput. Optim. Appl. 8(3), 423–452 (2011)

    Article  MathSciNet  Google Scholar 

  4. Facchinei, F., Sagratella, S.: On the computation of all solutions of jointly convex generalized Nash equilibrium problems. Optim. Lett. 5(3), 531–547 (2011)

    Article  MathSciNet  Google Scholar 

  5. Dreves, A., Kanzow, C., Stein, O.: Nonsmooth optimization reformulations of player convex generalized Nash equilibrium problems. J. Glob. Optim. 53(4), 587–614 (2012)

    Article  MathSciNet  Google Scholar 

  6. Clempner, J.B., Poznyak, A.S.: Convergence method, properties and computational complexity for Lyapunov games. Int. J. Appl. Math. Comput. Sci. 21(2), 349–361 (2011)

    Article  MathSciNet  Google Scholar 

  7. Gabriel, S.A., Siddiqui, S., Conejo, A.J., Ruiz, C.: Solving discretely-constrained Nash–Cournot games with an application to power markets. Netw. Spat. Econ. 13(3), 307–326 (2013)

    Article  MathSciNet  Google Scholar 

  8. Facchinei, F., Kanzow, C., Sagratella, S.: Solving quasi-variational inequalities via their kkt conditions. Math. Progr. 144(1–2), 369–412 (2014)

    Article  MathSciNet  Google Scholar 

  9. Clempner, J.B.: Setting Cournot vs. Lyapunov games stability conditions and equilibrium point properties. Int. Game Theory Rev. 17, 1–10 (2015)

    Article  Google Scholar 

  10. Clempner, J.B., Poznyak, A.S.: Computing the strong Nash equilibrium for Markov chains games. Appl. Math. Comput. 265, 911–927 (2015)

    MathSciNet  MATH  Google Scholar 

  11. Trejo, K.K., Clempner, J.B., Poznyak, A.S.: An optimal strong equilibrium solution for cooperative multi-leader-follower Stackelberg Markov chains games. Kibernetika 52(2), 258–279 (2016)

    MathSciNet  MATH  Google Scholar 

  12. Antipin, A.S.: An extraproximal method for solving equilibrium programming problems and games. Comput. Math. Math. Phys. 45(11), 1893–1914 (2005)

    MathSciNet  Google Scholar 

  13. Dreves, A.: Computing all solutions of linear generalized Nash equilibrium problems. Math. Methods Oper. Res. (2016). https://doi.org/10.1007/s00186-016-0562-0

    Article  MathSciNet  MATH  Google Scholar 

  14. Clempner, J.B., Poznyak, A.S.: Analysis of best-reply strategies in repeated finite Markov chains games. In: IEEE Conference on Decision and Control (2013)

  15. Clempner, J.B., Poznyak, A.S.: Convergence analysis for pure and stationary strategies in repeated potential games: Nash, Lyapunov and correlated equilibria. Expert Syst. Appl. 46, 474–484 (2016)

    Article  Google Scholar 

  16. Trejo, K.K., Clempner, J.B., Poznyak, A.S.: Computing the Lp-strong Nash equilibrium for Markov chains games. Appl. Math. Model. 41, 399–418 (2017)

    Article  MathSciNet  Google Scholar 

  17. Clempner, J.B., Poznyak, A.S.: Finding the strong Nash equilibrium: computation, existence and characterization for Markov games. J. Optim. Theory Appl. 186(3), 1029–1052 (2020)

    Article  MathSciNet  Google Scholar 

  18. Clempner, J.B., Poznyak, A.S.: A Tikhonov regularization parameter approach for solving Lagrange constrained optimization problems. Eng. Optim. 50(11), 1996–2012 (2018). https://doi.org/10.1080/0305215X.2017.1418866

    Article  MathSciNet  Google Scholar 

  19. Clempner, J.B., Poznyak, A.S.: A Tikhonov regularized penalty function approach for solving polylinear programming problems. J. Comput. Appl. Math. 328, 267–286 (2018)

    Article  MathSciNet  Google Scholar 

  20. Solis, C.U., Clempner, J.B., Poznyak, A.S.: Modeling multi-leader-follower non-cooperative Stackelberg games. Cybern. Syst. 47(8), 650–673 (2016)

    Article  Google Scholar 

  21. Clempner, J.B., Poznyak, A.S.: Analyzing an optimistic attitude for the leader firm in duopoly models: a strong Stackelberg equilibrium based on a Lyapunov game theory approach. Econ. Comput. Econ. Cybern. Stud. Res. 4(50), 41–60 (2016)

    Google Scholar 

  22. Tanaka, K., Yokoyama, K.: On \(\epsilon \)-equilibrium point in a noncooperative n-person game. J. Math. Anal. Appl. 160, 413–423 (1991)

    Article  MathSciNet  Google Scholar 

  23. Tanaka, K.: The closest solution to the shadow minimum of a cooperative dynamic game. Comput. Math. Appl. 18(1–3), 181–188 (1989)

    Article  MathSciNet  Google Scholar 

  24. Clempner, J.B.: Computing multiobjective Markov chains handled by the extraproximal method. Ann. Oper. Res. 271(2), 469–486 (2018)

    Article  MathSciNet  Google Scholar 

  25. Vasilyev, F.P., Khoroshilova, E.V., Antipin, S.: An extragradient method for finding the saddle point in an optimal control problem. Moscow Univ. Comput. Math. Cybern. 34(3), 113–118 (2010)

    Article  Google Scholar 

  26. Trejo, K.K., Clempner, J.B., Poznyak, A.S.: Computing the Stackelberg/Nash equilibria using the extraproximal method: convergence analysis and implementation details for Markov chains games. Int. J. Appl. Math. Comput. Sci. 25(2), 337–351 (2015)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Escuela Superior de Fsica y Matemticas, Instituto Politcnico Nacional, School of Physics and Mathematics, National Polytechnic Institute, Edificio 9 U.P. Adolfo Lopez Mateos, Col. San Pedro Zacatenco, 07730, Mexico City, Mexico

    Julio B. Clempner

Authors
  1. Julio B. Clempner
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Julio B. Clempner.

Additional information

Communicated by Kyriakos G. Vamvoudakis.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Clempner, J.B. A Proximal/Gradient Approach for Computing the Nash Equilibrium in Controllable Markov Games. J Optim Theory Appl 188, 847–862 (2021). https://doi.org/10.1007/s10957-021-01812-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-021-01812-3

Keywords

Mathematics Subject Classification