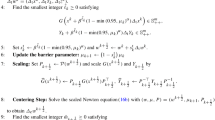Abstract
We propose a local convergence analysis of a primal–dual interior point algorithm for the solution of a bound-constrained optimization problem. The algorithm includes a regularization technique to prevent singularity of the matrix of the linear system at each iteration, when the second-order sufficient conditions do not hold at the solution. These conditions are replaced by a milder assumption related to a local error-bound condition. This new condition is a generalization of the one used in unconstrained optimization. We show that by an appropriate updating strategy of the barrier parameter and of the regularization parameter, the proposed algorithm owns a superlinear rate of convergence. The analysis is made thanks to a boundedness property of the inverse of the Jacobian matrix arising in interior point algorithms. An illustrative example is given to show the behavior and the gain obtained by this regularization strategy.

Similar content being viewed by others
References
Armand, P., Benoist, J.: A local convergence property of primal–dual methods for nonlinear programming. Math. Program. 115(2, Ser. A), 199–222 (2008). https://doi.org/10.1007/s10107-007-0136-2
Armand, P., Benoist, J., Dussault, J.P.: Local path-following property of inexact interior methods in nonlinear programming. Comput. Optim. Appl. 52(1), 209–238 (2012). https://doi.org/10.1007/s10589-011-9406-2
Armand, P., Benoist, J., Orban, D.: Dynamic updates of the barrier parameter in primal-dual methods for nonlinear programming. Comput. Optim. Appl. 41(1), 1–25 (2008). https://doi.org/10.1007/s10589-007-9095-z
Byrd, R.H., Liu, G., Nocedal, J.: On the local behaviour of an interior point method for nonlinear programming. In: Numerical Analysis 1997 (Dundee), Pitman Research Notes in Mathematical Series, vol. 380, pp. 37–56. Longman, Harlow (1998)
El-Bakry, A.S., Tapia, R.A., Tsuchiya, T., Zhang, Y.: On the formulation and theory of the Newton interior-point method for nonlinear programming. J. Optim. Theory Appl. 89(3), 507–541 (1996). https://doi.org/10.1007/BF02275347
Gould, N.I.M., Orban, D., Sartenaer, A., Toint, P.L.: Superlinear convergence of primal–dual interior point algorithms for nonlinear programming. SIAM J. Optim. 11(4), 974–1002 (2001). https://doi.org/10.1137/S1052623400370515
Gould, N.I.M., Orban, D., Sartenaer, A., Toint, P.L.: Componentwise fast convergence in the solution of full-rank systems of nonlinear equations. Math. Program. 92(3, Ser. B), 481–508 (2002). https://doi.org/10.1007/s101070100287
Tits, A.L., Wächter, A., Bakhtiari, S., Urban, T.J., Lawrence, C.T.: A primal–dual interior-point method for nonlinear programming with strong global and local convergence properties. SIAM J. Optim. 14(1), 173–199 (2003). https://doi.org/10.1137/S1052623401392123
Yamashita, H., Yabe, H.: Superlinear and quadratic convergence of some primal–dual interior point methods for constrained optimization. Math. Program. 75(3, Ser. A), 377–397 (1996). https://doi.org/10.1007/BF02592190
Hager, W.W., Zhang, H.: Self-adaptive inexact proximal point methods. Comput. Optim. Appl. 39(2), 161–181 (2008). https://doi.org/10.1007/s10589-007-9067-3
Esmaeili, H., Kimiaei, M.: A trust-region method with improved adaptive radius for systems of nonlinear equations. Math. Methods Oper. Res. 83(1), 109–125 (2016). https://doi.org/10.1007/s00186-015-0522-0
Fan, J., Yuan, Y.: A regularized Newton method for monotone nonlinear equations and its application. Optim. Methods Softw. 29(1), 102–119 (2014). https://doi.org/10.1080/10556788.2012.746344
Yamashita, N., Fukushima, M.: On the rate of convergence of the Levenberg–Marquardt method. In: Topics in Numerical Analysis, Computing Supplementa, vol. 15, pp. 239–249. Springer, Vienna (2001). https://doi.org/10.1007/978-3-7091-6217-0_18
Armand, P., Lankoandé, I.: An inexact proximal regularization method for unconstrained optimization. Math. Methods Oper. Res. 85(1), 43–59 (2017). https://doi.org/10.1007/s00186-016-0561-1
Li, D.H., Fukushima, M., Qi, L., Yamashita, N.: Regularized Newton methods for convex minimization problems with singular solutions. Comput. Optim. Appl. 28(2), 131–147 (2004). https://doi.org/10.1023/B:COAP.0000026881.96694.32
Ueda, K., Yamashita, N.: A regularized Newton method without line search for unconstrained optimization. Comput. Optim. Appl. 59(1–2), 321–351 (2014). https://doi.org/10.1007/s10589-014-9656-x
Altman, A., Gondzio, J.: Regularized symmetric indefinite systems in interior point methods for linear and quadratic optimization. Optim. Methods Softw. 11/12(1–4), 275–302 (1999). https://doi.org/10.1080/10556789908805754
Castro, J., Cuesta, J.: Quadratic regularizations in an interior-point method for primal block-angular problems. Math. Program. 130(2, Ser. A), 415–445 (2011). https://doi.org/10.1007/s10107-010-0341-2
Friedlander, M.P., Orban, D.: A primal–dual regularized interior-point method for convex quadratic programs. Math. Program. Comput. 4(1), 71–107 (2012). https://doi.org/10.1007/s12532-012-0035-2
Tseng, P., Yun, S.: Incrementally updated gradient methods for constrained and regularized optimization. J. Optim. Theory Appl. 160(3), 832–853 (2014). https://doi.org/10.1007/s10957-013-0409-2
Armand, P., Benoist, J.: Uniform boundedness of the inverse of a Jacobian matrix arising in regularized interior-point methods. Math. Program. 137(1–2, Ser. A), 587–592 (2013). https://doi.org/10.1007/s10107-011-0498-3
Tran, N.N.: Infeasibility detection and regularization strategies in nonlinear optimization. Ph.D. thesis, Université de Limoges, École Doctorale SISMI (2018). https://www.theses.fr/2018LIMO0059
Fuentes, M., Malick, J., Lemaréchal, C.: Descentwise inexact proximal algorithms for smooth optimization. Comput. Optim. Appl. 53(3), 755–769 (2012). https://doi.org/10.1007/s10589-012-9461-3
Humes Jr., C., Silva, P.J.S.: Inexact proximal point algorithms and descent methods in optimization. Optim. Eng. 6(2), 257–271 (2005). https://doi.org/10.1007/s11081-005-6798-9
Li, Y.J., Li, D.H.: Truncated regularized Newton method for convex minimizations. Comput. Optim. Appl. 43(1), 119–131 (2009). https://doi.org/10.1007/s10589-007-9128-7
Polyak, R.A.: Regularized Newton method for unconstrained convex optimization. Math. Program. 120(1, Ser. B), 125–145 (2009). https://doi.org/10.1007/s10107-007-0143-3
Santos, S.A., Silva, R.C.M.: An inexact and nonmonotone proximal method for smooth unconstrained minimization. J. Comput. Appl. Math. 269, 86–100 (2014). https://doi.org/10.1016/j.cam.2014.03.023
Shen, C., Chen, X., Liang, Y.: A regularized Newton method for degenerate unconstrained optimization problems. Optim. Lett. 6(8), 1913–1933 (2012). https://doi.org/10.1007/s11590-011-0386-z
Ueda, K., Yamashita, N.: Convergence properties of the regularized Newton method for the unconstrained nonconvex optimization. Appl. Math. Optim. 62(1), 27–46 (2010). https://doi.org/10.1007/s00245-009-9094-9
Parikh, N., Boyd, S.: Proximal algorithms. Found. Trends Optim. 1(3), 127–239 (2014). https://doi.org/10.1561/2400000003
Wang, C.Y., Zhang, J.Z., Zhao, W.L.: Two error bounds for constrained optimization problems and their applications. Appl. Math. Optim. 57(3), 307–328 (2008). https://doi.org/10.1007/s00245-007-9023-8
Tseng, P.: Error bounds and superlinear convergence analysis of some Newton-type methods in optimization. In: Nonlinear Optimization and Related Topics (Erice, 1998), Applied Optimization, vol. 36, pp. 445–462. Kluwer Academic Publishers, Dordrecht (2000). https://doi.org/10.1007/978-1-4757-3226-9_24
Horn, R.A., Johnson, C.R.: Matrix Analysis, 2nd edn. Cambridge University Press, Cambridge (2013). https://doi.org/10.1017/CBO9780511810817
Armand, P., Benoist, J., Orban, D.: From global to local convergence of interior methods for nonlinear optimization. Optim. Methods Softw. 28(5), 1051–1080 (2013). https://doi.org/10.1080/10556788.2012.668905
Armand, P., Omheni, R.: A mixed logarithmic barrier-augmented Lagrangian method for nonlinear optimization. J. Optim. Theory Appl. 173(2), 523–547 (2017). https://doi.org/10.1007/s10957-017-1071-x
Wächter, A., Biegler, L.T.: Line search filter methods for nonlinear programming: motivation and global convergence. SIAM J. Optim. 16(1), 1–31 (2005). https://doi.org/10.1137/S1052623403426556
Hock, W., Schittkowski, K.: Test Examples for Nonlinear Programming Codes. Lecture Notes in Economics and Mathematical Systems, vol. 187. Springer, Berlin, New York (1981)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Marco Antonio López-Cerdá.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A Appendix: Properties of the Regularized Jacobian Matrix
A Appendix: Properties of the Regularized Jacobian Matrix
The matrix of the linear system (3) is of the form
where \(w=(x,z)\in {\mathbb {R}}^{2n}\), \(H(w)\in {\mathbb {R}}^{n\times n}\) is symmetric, and \(\theta \ge 0\) is a regularization parameter. Two properties of this matrix are stated here. The statements of the following lemmas can be understood in a general framework of linear algebra. They are stated without proof. Detailed proofs can be found in [22, Lemma 5.8 and Lemma 5.9].
The first lemma is related to an upper bound of the inverse of \(J_\theta (w)\), for points on the boundary of the nonnegative orthant. This lemma is used in the proof of Lemma 5.1.
Lemma A.1
Let us define \({{{\mathcal {C}}}}=\{w=(x,z)\in {\mathbb {R}}^{2n}: 0\le x\perp z\ge 0\}\). Let \(w^*\in {{{\mathcal {C}}}}\) be such that
Let \({\mathcal {A}}=\{i: x^*_i = 0\}\) be the active set at \(x^*\) related to the bounds \(x\ge 0\). Let \(H: {\mathbb {R}}^{2n}\rightarrow {\mathbb {R}}^{n\times n}\) be a continuous function such that \(H(w)=H(w)^\top \). Assume that, for all \(u\in {\mathbb {R}}^n\) such that \(u_i=0\) for all \(i\in {\mathcal {A}}\), \(u^\top H(w^*) u\ge 0\). Then, for all \(\varepsilon \in ]0,a[\), there exists \(C>0\) such that for all \(w\in {B}(w^*,\varepsilon )\cap {{{\mathcal {C}}}}\) and \(\theta >0\), the matrix \(J_\theta (w)\) is nonsingular and
The second lemma also gives an upper bound of the inverse of \(J_\theta (w)\), but for points that are located in the interior of the positive orthant. This property is used in the proof of Lemma 5.2.
Lemma A.2
Let \(w^*=(x^*,z^*)\in {\mathbb {R}}^{2n}\) be such that
Let \(H: {\mathbb {R}}^{2n}\rightarrow {\mathbb {R}}^{n\times n}\) be a continuous function such that for all \(w\in {\mathbb {R}}^{2n}\), \(H(w)=H(w)^\top \). Let \(\theta :{\mathbb {R}}^{2n} \rightarrow {\mathbb {R}}_{++}\) be a continuous function such that \(\theta (w)\ge \gamma \Vert x\circ z\Vert ^t\), for all \(w\in {\mathbb {R}}^{2n}\), for some constants \(\gamma >0\) and \(t\in ]0,1[\). Assume that for all \(w\in {\mathbb {R}}^{2n}_{++}\), \(H(w)+X^{-1}Z\succeq 0\). For all \(w\in {\mathbb {R}}^{2n}_{++}\), the matrix \(J_{\theta (w)}(w)\) is nonsingular and for all \(\varepsilon \in ]0,a[\), there exists \(C>0\) such that for all \(w\in B(w^*,\varepsilon )\cap {\mathbb {R}}^{2n}_{++}\),
Rights and permissions
About this article
Cite this article
Armand, P., Tran, N.N. Local Convergence Analysis of a Primal–Dual Method for Bound-Constrained Optimization Without SOSC. J Optim Theory Appl 189, 96–116 (2021). https://doi.org/10.1007/s10957-021-01822-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-021-01822-1
Keywords
- Primal–dual method
- Interior point method
- Regularization
- Singular solutions
- Local error bounds
- Nonlinear optimization