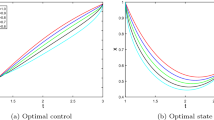
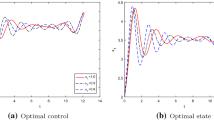
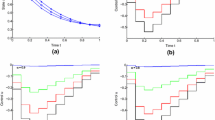
Abstract
In this paper, a numerical method is developed for solving a class of delay fractional optimal control problems involving nonlinear time-delay systems and subject to state inequality constraints. The fractional derivatives in this class of problems are described in the sense of Caputo, and they can be of different orders. First, we propose a numerical integration scheme for the fractional time-delay system and prove that the convergence rate of the numerical solution to the exact one is of second order based on Taylor expansion and linear interpolation. This gives rise to a discrete-time optimal control problem. Then, we derive the gradient formulas of the cost and constraint functions with respect to the decision variables and present a gradient computation procedure. On this basis, a gradient-based optimization algorithm is developed to solve the resulting discrete-time optimal control problem. Finally, several example problems are solved to demonstrate the effectiveness of the developed solution approach.








Similar content being viewed by others
References
Agrawal, O.P.: A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 78, 323–337 (2004)
Agrawal, O.P.: A formulation and numerical scheme for fractional optimal control problems. J. Vib. Control 14, 1291–1299 (2008)
Alipour, M., Rostamy, D., Baleanu, D.: Solving multi-dimensional fractional optimal control problems with inequality constraint by Bernstein polynomials operational matrices. J. Vib. Control 19, 2523–2540 (2013)
Alizadeh, A., Effati, S.: An iterative approach for solving fractional optimal control problems. J. Vib. Control 24, 18–36 (2018)
Bagley, R.L., Torvik, P.J.: A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 27, 201–210 (1983)
Baillie, R.T.: Long memory processes and fractional integration in econometrics. J. Econom. 75, 5–59 (1996)
Baleanu, D., Diethelm, K., Scalas, E., Trujillo, J.J.: Fractional Calculus: Models and Numerical Methods. World Scientific, Singapore (2012)
Balochian, S., Rajaee, N.: Fractional-order optimal control of fractional-order linear vibration systems with time delay. Int. J. Syst. Dyn. Appl. 7, 72–93 (2018)
Betts, J.T., Campbell, S., Thompson, K.: Optimal control software for constrained nonlinear systems with delays. In: Proceedings of IEEE Multi-conference on Systems and Control, pp. 444–449, Denver, USA (2011)
Bhrawy, A.H., Doha, E.H., Machado, J.A., Ezz-Eldien, S.S.: An efficient numerical scheme for solving multi-dimensional fractional optimal control problems with a quadratic performance index. Asian J. Control 17, 2389–2402 (2015)
Bhrawy, A.H., Ezz-Eldien, S.S.: A new Legendre operational technique for delay fractional optimal control problems. Calcolo 53, 521–543 (2016)
Cong, N.D., Tuan, H.T.: Existence, uniqueness, and exponential boundedness of global solution to delay fractional differential equations. Mediterr. J. Math. 14, 193 (2017)
Debeljković, D.: Time-Delay Systems. InTech, Rijeka (2011)
Dehghan, M., Hamedi, E., Khosravian-Arab, H.: A numerical scheme for the solution of a class of fractional variational and optimal control problems using the modified Jacobi polynomials. J. Vib. Control 22, 1547–1559 (2016)
Ezz-Eldien, S.S., Doha, E.H., Baleanu, D., Bhrawy, A.H.: A numerical approach based on Legendre orthonormal polynomials for numerical solutions of fractional optimal control problems. J. Vib. Control 23, 16–30 (2017)
Ghomanjani, F., Farahi, M.H., Gachpazan, M.: Optimal control of time-varying linear delay systems based on the Bezier curves. Comput. Appl. Math. 33, 687–715 (2014)
Gong, Z., Liu, C., Teo, K.L., Wang, S., Wu, Y.: Numerical solution of free final time fractional optimal control problems. Appl. Math. Comput. 405, 126270 (2021)
Guglielmi, N., Hairer, E.: Geometric proofs of numerical stability for delay equations. IMA J. Numer. Anal. 21, 439–450 (2001)
Guo, T.L.: The necessary conditions of fractional optimal control in the sense of Caputo. J. Optim. Theory Appl. 156, 115–126 (2013)
Hosseinpour, S., Nazemi, A.: A collocation method via block-pulse functions for solving delay fractional optimal control problems. IMA J. Math. Control Inf. 34, 1215–1237 (2016)
Hosseinpour, S., Nazemi, A., Tohidi, E.: Müntz–Legendre spectral collocation method for solving delay fractional optimal control problems. J. Comput. Appl. Math. 351, 344–363 (2019)
Kamocki, R.: On the existence of optimal solutions to fractional optimal control problems. Appl. Math. Comput. 235, 94–104 (2014)
Kamocki, R.: Pontryagin maximum principle for fractional ordinary optimal control problems. Math. Methods Appl. Sci. 37, 1668–1686 (2014)
Kamocki, R., Majewski, M.: Fractional linear control systems with Caputo derivative and their optimization. Optim. Control Appl. Methods 36, 953–967 (2015)
Kibass, A.A., Srivastava, A.M., Trujillo, I.I.: Theory and Application of Fractional Differential Equations. Elsevier, New York (2006)
Kumar, M.: Optimal design of fractional delay FIR filter using cuckoo search algorithm. Int. J. Circuit Theory Appl. 46, 2364–2379 (2018)
Laforgia, A., Natalini, P.: Exponential, gamma and polygamma functions: simple proofs of classical and new inequalities. J. Math. Anal. Appl. 407, 459–504 (2013)
Lenz, S.M., Schlöder, J.P., Bock, H.G.: Numerical computation of derivatives in systems of delay differential equations. Math. Comput. Simul. 96, 124–156 (2014)
Li, W., Wang, S., Rehbock, V.: A 2nd-order one-step numerical integration scheme for a fractional differential equation. Numer. Algebra Control Optim. 7, 273–287 (2017)
Li, W., Wang, S., Rehbock, V.: Numerical solution of fractional optimal control. J. Optim. Theory Appl. 180, 556–573 (2019)
Magin, R.L.: Fractional calculus in bioengineering. Crit. Rev. Biomed. Eng. 32, 1–104 (2004)
Martin, R., Quintana, J.J., Ramos, A., de la Nuez, I.: Modeling electrochemical double layer capacitor, from classical to fractional impedance. In: Proceedings of the IEEE Mediterranean Electrotechnical Conference, pp. 61–66, Ajaccio, France (2008)
Marzban, H.R.: Solution of a specific class of nonlinear fractional optimal control problems including multiple delays. Optim. Control Appl. Methods 42, 2–29 (2021)
Marzban, H.R.: A new fractional orthogonal basis and its application in nonlinear delay fractional optimal control problems. ISA Trans. 114, 106–119 (2021)
Marzban, H.R., Malakoutikhah, F.: Solution of delay fractional optimal control problems using a hybrid of block-pulse functions and orthonormal Taylor polynomials. J. Frankl. Inst. 356, 8182–8251 (2019)
Marzban, H.R., Pirmoradian, H.: A direct approach for the solution of nonlinear optimal control problems with multiple delays subject to mixed state-control constraints. Appl. Math. Model. 53, 189–213 (2018)
Mohammadzadeh, R., Lakestani, M.: Optimal control of linear time-delay systems by a hybrid of block-pulse functions and biorthogonal cubic Hermite spline multiwavelets. Optim. Control Appl. Methods 39, 357–376 (2018)
Moradi, L., Mohammadi, F., Baleanu, D.: A direct numerical solution of time-delay fractional optimal control problems by using Chelyshkov wavelets. J. Vib. Control 25, 310–324 (2019)
Mu, P., Wang, L., Liu, C.: A control parameterization method to solve the fractional-order optimal control problem. J. Optim. Theory Appl. 187, 234–247 (2020)
Nazemi, A., Mansoori, M.: Solving optimal control problems of the time-delayed systems by Haar wavelet. J. Vib. Control 22, 2657–2670 (2016)
Nocedal, J., Wright, S.J.: Numerical Optimization. Springer, New York (2006)
Pooseh, S., Almieda, R., Torres, D.F.M.C.: Fractional order optimal control problems with free terminal time. J. Ind. Manag. Optim. 10, 363–381 (2014)
Rahimkhani, P., Ordokhani, Y., Babolian, E.: An efficient approximate method for solving delay fractional optimal control problems. Nonlinear Dyn. 86, 1649–1661 (2016)
Safaie, E., Farahi, M.H., Ardehaie, M.F.: An approximate method for numerically solving multi-dimensional delay fractional optimal control problems by Bernstein polynomials. Comput. Appl. Math. 34, 831–846 (2015)
Salati, A.B., Shamsi, M., Torres, D.F.M.: Direct transcription methods based on fractional integral approximation formulas for solving nonlinear fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul. 67, 334–350 (2019)
Sweilam, N.H., AL-Mekhlafi, S.M.: Optimal control for a time delay multi-strain tuberculosis fractional model: a numerical approach. IMA J. Math. Control Inf. 36, 317–340 (2019)
Tang, X., Liu, Z., Wang, X.: Integral fractional pseudospectral methods for solving fractional optimal control problems. Automatica 62, 304–311 (2015)
Tang, X., Shi, Y., Wang, L.L.: A new framework for solving fractional optimal control problems using fractional pseudospectral method. Automatica 78, 333–340 (2017)
Teo, K.L., Li, B., Yu, C., Rehbock, V.: Applied and Computational Optimal Control. Springer, Berlin (2021)
Tricaud, C., Chen, Y.: An approximate method for numerically solving fractional order optimal control problems of general form. Comput. Math. Appl. 59, 1644–1655 (2010)
Tyrtyshnikov, E.E.: A Brief Introduction to Numerical Analysis. Birkhäuser, Boston (1997)
Wang, Z., Hong, X., Shi, G.: Analysis of nonlinear dynamics and chaos in a fractional order financial system with time delay. Comput. Math. Appl. 62, 1531–1539 (2011)
Yu, C., Lin, Q., Loxton, R., Teo, K.L., Wang, G.: A hybrid time-scaling transformation for time-delay optimal control problems. J. Optim. Theory Appl. 169, 876–901 (2016)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11771008), the Australian Research Council (No. DP190103361), the China Scholarship Council (No. 201902575002), and the Natural Science Foundation of Shandong Province, China (Nos. ZR2017MA005 and ZR2019MA031).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Ebrahim Sarabi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Theorem 3.1
We will prove the theorem in the following steps.
1.1 Step 1: Preliminaries
For \(k=1,\ldots ,N\), define \({\tilde{C}}^k=({\tilde{c}}_1^k,\ldots ,{\tilde{c}}_n^k)^\top \), where
Note that this vector can be regarded as a disturbance of vector \(C^k\) defined in (22). Furthermore, by using linear interpolation, \(x(s^i_{kl})\), \(x(s^i_{kl}-\tau )\), \(u(s^i_{kl})\) and \(u(s^i_{kl}-\sigma )\) in (13) can be, respectively, expressed as:
and
for all feasible i, k and l, where \(u^i_{kl}\) and \({\tilde{u}}^i_{kl_\sigma }\) are as defined in (14) and (16), respectively; and \(1^r\) is a column vector of all ones in \({\mathbb {R}}^r\).
1.2 Step 2: The Truncation Error \(R^i_k\) is of Order \({\mathcal {O}}(h^2)\)
Let \(i\in \{1,\ldots ,n\}\), \(k\in \{1,\ldots ,N\}\) and \(l\in \{1,\ldots ,k\}\). From (11), we have
By Assumption 2.1, f is twice continuously differentiable. Thus, \(c^i_{kl}\) is bounded on \([-\tau ,T]\). Let \({\bar{c}}=\max \nolimits _{\begin{array}{c} i\in \{1,\ldots ,n\}\\ k\in \{1,\ldots ,N\} \end{array}}\max \nolimits _{l\ \in \{1,\ldots ,k\}}|c^i_{kl}|\). Then, from the definition of \(R^i_k\), we have
Recall that \(\alpha _i\in ]0,1]\) for \(i=1,\ldots ,n\). Then, it follows from [27] that \(\varGamma (\alpha _i+1)\in [2^{\alpha _i-1},1]\). Also, it is obvious that \(T^{\alpha _i}\in ]1,T]\). Choosing \({\bar{C}}=2{\bar{c}}T\) gives
1.3 Step 3: \(B^k\) is Non-singular
By Assumption 2.1, f is twice continuously differentiable in x(t) and \(x(t-\tau )\). Thus, \(\displaystyle \frac{\displaystyle \partial f_i}{\displaystyle \partial x_p}\) and \(\displaystyle \frac{\displaystyle \partial f_i}{\displaystyle \partial {\tilde{x}}_p}\) are bounded on [0, T] for \(i=1,\ldots ,n\). Let
Note that \(\rho ^i_{kk}\in ]0,1[\) and \({\bar{\rho }}^i_{kk_\tau }\in ]0,1]\) for all feasible i and k. It follows from (21) that
Let \({\hat{h}}_i=\bigg (\displaystyle \frac{\displaystyle \varGamma (\alpha _i+1)}{\displaystyle 2nM}\bigg )^{\displaystyle \frac{\displaystyle 1}{\displaystyle \alpha _i}}\) and \({\hat{h}}=\min \limits _{i\in \{1,\ldots ,n\}}{\hat{h}}_i\). Then, for all \(h<{\hat{h}}\), \(\sum \limits _{p=1}^n|b^k_{ip}|<1,\ i=1,\ldots ,n.\) Since \(1-b^k_{ii}\ge 1-|b^k_{ii}|\), we have, for all \(i=1,\ldots ,n\),
which implies that matrix \(B^k\) is strictly diagonally dominant. By the Levy–Desplanques theorem [51], \(B^k\) is non-singular.
1.4 Step 4: Base Case for (23)
For \(k=1\), it follows from (13) that, for \(i=1,\ldots ,n\),
Substituting (49)–(52) with \(k=l=1\) in (54) and applying Taylor expansion yield
Recall that W is compact. By Assumption 2.1 and (53), (55) can be simplified as
Thus, \(x(t_1)\) is a solution of the following linear equations:
Since matrix \(B^1\) is non-singular when \(h<{\hat{h}}\) (recall that \({\hat{h}}\) is defined in Step 3), (20) as well as (57) has a unique solution. Thus, combining (57) with (20) yields
This proves that (23) holds for \(k=1\) when \(h<{\hat{h}}\).
1.5 Step 5: Inductive Step for (23)
We now consider the case of \(k\ge 2\). Assume that, for \(l=1,\ldots ,k-1\),
when \(h<{\hat{h}}\).
From (13) and Step 2, we have
where
and
Using (49)–(52) and applying Taylor expansion give
By Assumption 2.1, Step 2, and (10), we can simplify (61) as:
Furthermore, using a Taylor expansion, we obtain
where
\(\xi ^{k-1}\) and \(\zeta ^{k-1}\) are two points between \(x(t_{k-1})\) and \(x^{k-1}\); and \(\nu ^{k-1}\) is a point between \(x(s^i_{kk}-\tau )\) and \({\tilde{x}}^i_{kk_\tau }\). By Assumption 2.1 and (59), \(|{\bar{R}}^i_k|={\mathcal {O}}(h^2)\). Similarly, we have, for \(p=1,\ldots ,n\),
and
Using estimations (63)–(65), (62) can be rewritten as:
Now, we consider the estimation for \(A^i_{k-1}\). By Assumption 2.1 and (49)–(51), we have
where
and \(\theta ^i(\cdot )\) is as defined in (34). From (59) and Assumption 2.1, we obtain \(|{\tilde{R}}^i_{kl}|={\mathcal {O}}(h^2)\). Furthermore, using a similar proof as given for Step 2, we have
Thus,
Substituting (66) and (67) in (60) gives
Combining this equation with (20) and using (59), we have
from which we immediately infer that (58) holds for \(l=k\). \(\square \)
Rights and permissions
About this article
Cite this article
Liu, C., Gong, Z., Yu, C. et al. Optimal Control Computation for Nonlinear Fractional Time-Delay Systems with State Inequality Constraints. J Optim Theory Appl 191, 83–117 (2021). https://doi.org/10.1007/s10957-021-01926-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-021-01926-8
Keywords
- Fractional time-delay system
- Fractional optimal control
- Inequality constraint
- Numerical integration
- Numerical optimization