Skip to main content
Springer Nature Link
Log in

Sustainable Cooperation in Dynamic Games on Event Trees with Players’ Asymmetric Beliefs

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

We built a time-consistent cooperative solution for the class of dynamic games played over event trees in the context where the tree structure is given, but the players have different beliefs about the transition probabilities between nodes. Our three-step approach is as follows. First, we consider three alternative methods for aggregating the players’ beliefs and assume that the players agree to adopt one of them if they decide to cooperate. Second, we determine the Nash bargaining outcomes for the whole duration of the game. Finally, to insure sustainability of cooperation throughout the whole duration of the game, we propose two time-consistent decompositions over nodes of each player’s cooperative share, namely a proportion-consistent and a node-consistent allocation schemes. We illustrate our results with a simple Cournot oligopoly with capacity constraints.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. In this paper, we do not consider imprecise probabilities and refer the interested reader to [31] for a discussion on their use in event trees.

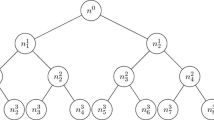
  2. We call the strategy \( S \)-adapted to highlight that at each period we have a Sample of events corresponding to the nodes.

  3. We use term “belief aggregation” in Sect. 3 when describing the methods of aggregating probability distributions, whereas in the literature the term “opinion pooling” is used ([4, 26, 27]). To avoid confusion, we use the “opinion pooling” technique to aggregate players’ beliefs on transition probabilities but use the term “belief aggregation” to be in line with the theory of dynamic games with imperfect information.

  4. Updating the weights may be considered only in the cases of linear and geometric belief aggregations. In multiplicative belief aggregation the weights are not used. The “calibrating” probability function plays the role of weights.

  5. See [12] for a definition of the Nash bargaining solution.

  6. In the considered problem, only the regular case is meaningful. Therefore, the non-regular case, when \(\nu _{0}=0\), is omitted here.

  7. One can think of these additional properties as a refinement approach of the IDP.

References

  1. Avrachenkov, K., Elias, J., Martignon, F., Neglia, G., Petrosyan, L.: Cooperative network design: a Nash bargaining solution approach. Comput. Netw. 83, 265–279 (2015)

    Article  Google Scholar 

  2. Clemen, R.T., Winkler, R.L.: Combining probability distributions from experts in risk analysis. Risk Anal. 19(2), 187–203 (1999)

    Google Scholar 

  3. Dietrich, F.: Bayesian group belief. Soc. Choice Welf. 35(4), 595–626 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  4. Dietrich, F., List, C.: Probabilistic opinion pooling. In: Hajek, A., Hitchcock, C. (eds.) Oxford Handbook of Probability and Philosophy. Oxford University Press, Oxford (2016)

    Google Scholar 

  5. French, S.: Group consensus probability distributions: a critical survey. In: Bernardo, D., DeGroot, M., Smith, A. (eds.) Bayesian Statistics: Proceedings of the Second Valencia International Meeting, pp. 183–201. North-Holland, Amsterdam (1985)

    Google Scholar 

  6. Genc, T., Reynolds, S., Sen, S.: Dynamic oligopolistic games under uncertainty: a stochastic programming approach. J. Econ. Dyn. Control 31, 55–80 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Genc, T., Sen, S.: An analysis of capacity and price trajectories for the Ontario electricity market using dynamic Nash equilibrium under uncertainty. Energy Econ. 30, 173–191 (2008)

    Article  Google Scholar 

  8. Gromova, E., Plekhanova, T.: On the regularization of a cooperative solution in a multistage game with random time horizon. Discret. Appl. Math. 255, 40–55 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  9. Haurie, A., Krawczyk, J.B., Zaccour, G.: Games and Dynamic Games. World Scientific, Singapore (2012)

    Book  MATH  Google Scholar 

  10. Haurie, A., Zaccour, G., Smeers, Y.: Stochastic equilibrium programming for dynamic oligopolistic markets. J. Optim. Theory Appl. 66(2), 243–253 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  11. Madansky, A.: Externally Bayesian Groups. RAND Corporation, RM-4141-PR, Santa Monica (1964)

    Google Scholar 

  12. Nash, J.: The bargaining problem. Econometrica 18(2), 155–162 (1950)

    Article  MathSciNet  MATH  Google Scholar 

  13. Ouchi, F.: A Literature Review on the Use of Expert Opinion in Probabilistic Risk Analysis. World Bank, Washington, DC (2004)

    Book  Google Scholar 

  14. Parilina, E., Tampieri, A.: Stability and cooperative solution in stochastic games. Theor. Decis. 84, 601–625 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  15. Parilina, E., Zaccour, G.: Approximated cooperative equilibria for games played over event trees. Oper. Res. Lett. 43(5), 507–513 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  16. Parilina, E., Zaccour, G.: Node-consistent core for games played over event trees. Automatica 53, 304–311 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  17. Parilina, E., Zaccour, G.: Strategic support of node-consistent cooperative outcomes in dynamic games played over event trees. Int. Game Theory Rev. 18(2), 1640002 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  18. Parilina, E., Zaccour, G.: Node-consistent Shapley value for games played over event trees with random terminal time. J. Optim. Theory Appl. 175(1), 236–254 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  19. Petrosyan, L.: Stable solutions of differential games with many participants. Viestnik Leningrad Univ. 19, 46–52 (1977)

    Google Scholar 

  20. Petrosyan, L., Danilov, N.A.: Time-consistent solutions of non-antagonistic differential games with transferable payoffs. Viestnik Leningrad Univ. 1, 46–54 (1979)

    Google Scholar 

  21. Petrosyan, L., Zaccour, G.: Cooperative differential games with transferable payoffs. In: Basar, T., Zaccour, G. (eds.) Handbook of Dynamic Game Theory, pp. 595–632. Springer, Cham (2018)

    Chapter  Google Scholar 

  22. Pineau, P.O., Rasata, H., Zaccour, G.: Impact of some parameters on investments in oligopolistic electricity markets. Eur. J. Oper. Res. 213(1), 180–195 (2011)

    Article  MathSciNet  Google Scholar 

  23. Reddy, P.V., Shevkoplyas, E., Zaccour, G.: Time-consistent Shapley value for games played over event trees. Automatica 49(6), 1521–1527 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  24. Reddy, P.V., Zaccour, G.: Open-loop and feedback Nash equilibria in constrained linear-quadratic dynamic games played over event trees. Automatica 107, 162–174 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  25. Rosen, J.B.: Existence and uniqueness of equilibrium points for concave n-person games. Econometrica 33(3), 520–534 (1965)

    Article  MathSciNet  MATH  Google Scholar 

  26. Stewart, R.T., Quintana, I.O.: Probabilistic opinion pooling with imprecise probabilities. J. Philos. Log. 47, 17–45 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  27. Stone, M.: The opinion pool. Ann. Math. Stat. 32(4), 1339–1342 (1961)

    Article  MathSciNet  MATH  Google Scholar 

  28. Yeung, D., Petrosyan, L.: Proportional time-consistent solutions in differential games. In: Contributions to the Theory of Games II, Annals of Mathematics Studies, pp. 254–256. Saint Petersburg (2001)

  29. Yeung, D., Petrosyan, L.: Subgame Consistent Economic Optimization. Birkhauser, Boston (2012)

    Book  MATH  Google Scholar 

  30. Yeung, D.W., Petrosyan, L.A.: Nontransferable utility cooperative dynamic games. In: Basar, T., Zaccour, G. (eds.) Handbook of Dynamic Game Theory, pp. 633–670. Springer, Cham (2018)

    Chapter  Google Scholar 

  31. You, X., Tonon, F.: Event-tree analysis with imprecise probabilities. Risk Anal. 32(2), 331–344 (2012)

    Article  Google Scholar 

  32. Zaccour, G.: Théorie des jeux et marchés énergétiques: marché européen de gaz naturel et échanges d’électricité, Ph.D. Thesis. HEC Montréal (1987)

  33. Zaccour, G.: Time consistency in cooperative differential games: a tutorial. INFOR 46(1), 81–92 (2008)

    MathSciNet  Google Scholar 

  34. Zaccour, G.: Sustainability of cooperation in dynamic games played over event trees. In: Roderick, R.M., Belair, J. (eds.) Recent Progress and Modern Challenges in Applied Mathematics, Modeling and Computational Science, Fields Institute Communications Series, pp. 419–437. Springer, Cham (2017)

    Google Scholar 

Download references

Acknowledgements

We would like to thank the editor and the two anonymous reviewers for their helpful comments. This research was partially conducted during the research stay of the first author at GERAD. The work of the first author was supported by the Shandong Province “Double-Hundred Talent Plan” (No. WST2017009). The work of the second author is supported by NSERC, Canada, Grant RGPIN-2016-04975.

Author information

Authors and Affiliations

  1. Saint Petersburg State University, Saint Petersburg, Russia

    Elena M. Parilina

  2. Institute of Applied Mathematics of Shandong, School of Mathematics and Statistics, Qingdao University, Qingdao, People’s Republic of China

    Elena M. Parilina

  3. Chair in Game Theory and Management, GERAD, HEC Montréal, Montreal, Canada

    Georges Zaccour

Authors
  1. Elena M. Parilina
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Georges Zaccour
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Elena M. Parilina.

Additional information

Communicated by Felix L. Chernousko.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Parilina, E.M., Zaccour, G. Sustainable Cooperation in Dynamic Games on Event Trees with Players’ Asymmetric Beliefs. J Optim Theory Appl 194, 92–120 (2022). https://doi.org/10.1007/s10957-022-02010-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-022-02010-5

Keywords

Mathematics Subject Classification