On an Optimal Control Problem Describing Lactate Transport Inhibition

Abstract

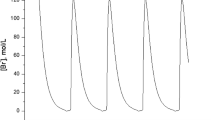
In this paper, the effect of inhibition of monocarboxylate transporters on intracellular and capillary lactate concentrations is investigated using an optimal control problem. A control term representing the concentration of the inhibitor is used in an ODE model that models lactate kinetics between the cell and the capillary. Finally, some numerical simulations were performed to confirm the efficiency of the control term for the problem.

Appendices

Appendix A

Proof of Theorem 2.2

Proof

• The solution is nonnegative. System (1.4)–(1.6) can be viewed as

  $$\begin{aligned} \begin{array}{lll} u^{\prime }(t)=f(t,u(t),v(t)) \\ v^{\prime }(t) =g(t,u(t),v(t)). \end{array} \end{aligned}$$

Using Assumption (E), for $u=0,\, v\ge 0$, then

$$\begin{aligned} f(t,0,v) =J +\kappa \dfrac{v}{k^{\prime }+v}\ge 0. \end{aligned}$$

For $u\ge 0,\, v=0$ and using Assumption (E), see that F is a positive function and $L >0$. Thus,

$$\begin{aligned} g(t,u,0) = \frac{FL}{\epsilon } + \frac{\kappa }{\epsilon }(1-\gamma w)\dfrac{u}{k +u}\ge 0. \end{aligned}$$

Hence, the system is quasipositive and so the solution

$$\begin{aligned} (u,v)\in \mathbb {R}_{+}\times \mathbb {R}_{+}\quad \forall \, t>0. \end{aligned}$$

• Existence of solution.

System (1.4)–(1.6) can be rewritten in the form

$$\begin{aligned} \left\{ \begin{array}{lll} X^{\prime }(t)=F(t,X(t)) \\ X(0)=X_0, \end{array}\right. \end{aligned}$$

where $X(t):=(u(t),v(t))$ and $F(t,X(t)):= (f(t,u,v),g(t,u,v))$. We know that for nonnegative $u_1$ and $u_2$

$$\begin{aligned} \dfrac{u_1}{k+u_1}-\dfrac{u_2}{k +u_2}=\dfrac{u_1(k+u_2)-u_2(k+u_1)}{(k+u_1)(k+u_2)} =\dfrac{k(u_1-u_2)}{(k+u_1)(k+u_2)} \end{aligned}$$

and for nonnegative $v_1$ and $v_2$

$$\begin{aligned} \dfrac{v_1}{k^{\prime }+v_1}-\dfrac{v_2}{k^{\prime } +v_2}\hspace{0.5cm} = \dfrac{k^{\prime }(v_1-v_2)}{(k^{\prime }+v_1)(k^{\prime }+v_2)}. \end{aligned}$$

As well, using Assumption (E), we have

$$\begin{aligned} \begin{array}{cc} \displaystyle \left| J(t,u_1)- J(t,u_2) -\kappa (1-\gamma w)\dfrac{k(u_1-u_2)}{(k+u_1)(k+u_2)} +\kappa \dfrac{k^{\prime }(v_1-v_2)}{(k^{\prime }+v_1)(k^{\prime }+v_2)}\right| \\ \displaystyle \lesssim |u_1-u_2| +|v_1-v_2| \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{cc} \displaystyle \dfrac{1}{\epsilon }\left| F(v_1-v_2) +\kappa (1-\gamma w)\dfrac{k(u_1-u_2)}{(k+u_1)(k+u_2)} -\kappa \dfrac{k^{\prime }(v_1-v_2)}{(k^{\prime }+v_1)(k^{\prime }+v_2)}\right| \\ \displaystyle \lesssim |u_1-u_2| +|v_1-v_2| \end{array} \end{aligned}$$

We deduce that F is globally Lipschitz with respect to u and v, so System (1.4)–(1.6) admits a unique solution $(u,v)\in C^1([0,T],\mathbb {R}_{+})^2$.

• Continuous dependence on control.

Let $w_1, w_2$ be two controls in $\mathcal {W}_{ad}$ and $(u_1,v_1)$, $(u_2,v_2)$ be their corresponding solutions of System (1.4)–(1.6) with same initial data. Set $u=u_1-u_2$, $v = v_1 - v_2$, and $w= w_1 -w_2$, then we have

$$\begin{aligned}{} & {} u^{\prime } =J(t,u_1) - J(t,u_2) -\kappa \left( \dfrac{ku}{(k+u_1)(k+u_2)}\right. \nonumber \\{} & {} \left. -\gamma \dfrac{k\left( w_1 u +u_2 w\right) +w u_1u_2}{(k+u_1)(k+u_2)} -\dfrac{k^{\prime }v}{(k^{\prime }+v_1)(k^{\prime }+v_2)}\right) \end{aligned}$$

(A.1)

and

$$\begin{aligned} \epsilon v^{\prime } =-F v + \kappa \left( \dfrac{ku}{(k+u_1)(k+u_2)} -\gamma \dfrac{k\left( w_1 u +u_2 w\right) +w u_1u_2}{(k+u_1)(k+u_2)} -\dfrac{k^{\prime }v}{(k^{\prime }+v_1)(k^{\prime }+v_2)}\right) . \end{aligned}$$

(A.2)

Step one. Multiply Equation (A.1) by u in $\mathbb {R_{+}}$, we find

$$\begin{aligned} \displaystyle ((u^{\prime },u))= & {} \left( \left( J(t,u_1) - J(t,u_2),u\right) \right) \\{} & {} -\kappa \left( \left( \dfrac{ku}{(k+u_1)(k+u_2)},u\right) \right) -\kappa \gamma \left( \left( \dfrac{wu_1u_2}{(k+u_1)(k+u_2)},u\right) \right) \\{} & {} -\kappa \gamma \left( \left( \dfrac{k\left( w_1 u +u_2 w\right) }{(k+u_1)(k+u_2)},u\right) \right) \\{} & {} -\kappa \left( \left( \dfrac{k^{\prime }v}{(k^{\prime }+v_1)(k^{\prime }+v_2)},u\right) \right) , \end{aligned}$$

Thanks to Cauchy–Schwarz inequality, we get

$$\begin{aligned} \displaystyle \dfrac{1}{2}\dfrac{\textrm{d}}{\textrm{d}t}\left\Vert u\right\Vert ^2\le & {} \left\Vert J(t,u_1) - J(t,u_2)\right\Vert \left\Vert u\right\Vert +\kappa k \left\Vert \dfrac{u}{(k+u_1)(k+u_2)}\right\Vert \left\Vert u\right\Vert \\{} & {} +\kappa \gamma \left\Vert \dfrac{wu_1u_2}{(k+u_1)(k+u_2)}\right\Vert \left\Vert u\right\Vert \\{} & {} +\kappa k \gamma \left\Vert \dfrac{w_1 u }{(k+u_1)(k+u_2)}\right\Vert \left\Vert u\right\Vert \\{} & {} +\kappa \gamma \left\Vert \dfrac{u_2 w}{(k+u_1)(k+u_2)}\right\Vert \left\Vert u\right\Vert +\kappa k^{\prime }\left\Vert \dfrac{k^{\prime }v}{(k^{\prime }+v_1)(k^{\prime }+v_2)}\right\Vert \left\Vert u\right\Vert . \end{aligned}$$

Now using Assumption (E) and Young’s inequality, we have

$$\begin{aligned} \dfrac{\textrm{d}}{\textrm{d}t}\left\Vert u\right\Vert ^2 \lesssim \left\Vert u\right\Vert ^2 + \left\Vert w\right\Vert ^2 +\left\Vert v\right\Vert ^2. \end{aligned}$$

(A.3)

On the other hand, multiplying Equation (A.2) by v in $\mathbb {R}_+$, using Assumption (E) and Young’s inequality, we get

$$\begin{aligned} \dfrac{\textrm{d}}{\textrm{d}t}\left\Vert v\right\Vert ^2 \lesssim \left\Vert u\right\Vert ^2 + \left\Vert w\right\Vert ^2 +\left\Vert v\right\Vert ^2. \end{aligned}$$

(A.4)

Combining Equation (A.3) and Equation (A.4), then integrating over [0, t], where $t \in [0,T]$, we get

$$\begin{aligned} \left\Vert u(t)\right\Vert ^2 +\left\Vert v(t)\right\Vert ^2 \lesssim \int _0^t\left\Vert w(s)\right\Vert ^2\textrm{d}s +\int _0^t\left( \left\Vert u(s)\right\Vert ^2 +\left\Vert v(s)\right\Vert ^2\right) \textrm{d}s. \end{aligned}$$

So, owing to Gronwall’s inequality, we obtain

$$\begin{aligned} \left\Vert u(t)\right\Vert ^2 +\left\Vert v(t)\right\Vert ^2 \lesssim \left\Vert w\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}e^{ct},\quad t\in [0,T]. \end{aligned}$$

(A.5)

On the other hand, since

$$\begin{aligned} \left\Vert u\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)} =\int _0^t \left\Vert u(s)\right\Vert ^2 \textrm{d}s, \end{aligned}$$

then, using Equation (A.5), we find

$$\begin{aligned} \int _0^t \left\Vert u(s)\right\Vert ^2 \textrm{d}s \lesssim \int _0^t \left\Vert w\right\Vert ^2_{L^2(0,s;\mathbb {R}_+)}e^{cs} \textrm{d}s\lesssim \left\Vert w\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}(e^{ct}-1), \quad \forall t\in [0,T]. \end{aligned}$$

(A.6)

Similarly, we have

$$\begin{aligned} \left\Vert v\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}\lesssim \left\Vert w\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}(e^{ct}-1). \end{aligned}$$

(A.7)

Step two. Similarly to step one, multiplying Equation (A.1) and Equation (A.2) by $u^{\prime }$ and $v^{\prime }$, respectively, we get

$$\begin{aligned} \begin{array}{lll} \displaystyle \left\Vert u^{\prime }\right\Vert ^2 \le \displaystyle \left\Vert J(t,u_1) -J(t,u_2)\right\Vert \left\Vert u^{\prime }\right\Vert + c\left\Vert u\right\Vert \left\Vert u^{\prime }\right\Vert +c\left\Vert w\right\Vert \left\Vert u^{\prime }\right\Vert +c\left\Vert v\right\Vert \left\Vert u^{\prime }\right\Vert \\ \displaystyle \lesssim \left\Vert u\right\Vert \left\Vert u^{\prime }\right\Vert +\left\Vert w\right\Vert \left\Vert u^{\prime }\right\Vert +\left\Vert v\right\Vert \left\Vert u^{\prime }\right\Vert . \end{array} \end{aligned}$$

Let $\delta >0$. Applying Young’s inequality, we obtain

$$\begin{aligned} (1-c \delta )\left\Vert u^{\prime }\right\Vert ^2 \displaystyle \lesssim \left\Vert u\right\Vert ^2 +\left\Vert w\right\Vert ^2 +\left\Vert v\right\Vert ^2. \end{aligned}$$

where $c >0$ is a constant independent of $\delta$. Choosing $\delta<<1$ so that $1 -c \delta =\dfrac{1}{2}$, we obtain

$$\begin{aligned} \dfrac{1}{2}\left\Vert u^{\prime }\right\Vert ^2 \displaystyle \lesssim \left\Vert u\right\Vert ^2 +\left\Vert w\right\Vert ^2 +\left\Vert v\right\Vert ^2. \end{aligned}$$

(A.8)

By similar way, we obtain

$$\begin{aligned} \epsilon \left\Vert v^{\prime }\right\Vert ^2\lesssim \left\Vert v\right\Vert ^2 +c\left\Vert u\right\Vert ^2+\left\Vert w\right\Vert ^2. \end{aligned}$$

(A.9)

Further, integrating (A.8) and (A.9) over $[0,t], \, t\in [0,T]$, and using (A.5), we get

$$\begin{aligned} \begin{array}{lll} \displaystyle \left\Vert u^{\prime }\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})}\lesssim \left\Vert u\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})} +\left\Vert v\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})} +\left\Vert w\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})} \\ \displaystyle \hspace{2.3cm}\lesssim \left\Vert w\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})} \end{array} \end{aligned}$$

and

$$\begin{aligned} \epsilon \left\Vert v^{\prime }\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})} \lesssim \left\Vert v\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})} +\left\Vert u\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})} +\left\Vert w\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})}, \end{aligned}$$

and hence,

$$\begin{aligned} \left\Vert v^{\prime }\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})}\lesssim \left\Vert w\right\Vert ^2_{L^2(0,t;\mathbb {R}_{+})}. \end{aligned}$$

$\square$

Proof of Theorem 4.1

Proof

Let $(U_1,V_1)$, $(U_2,V_2)$ be two solutions of System (4.1)–(4.3), which can be written in the form

$$\begin{aligned} X^{\prime }=H(t,X(t)), \end{aligned}$$

where $X =(U,V)$ and $H(t,U,V)=(F(t,U,V),G(t,U,V))$, we know that

$$\begin{aligned} \begin{array}{llll} \displaystyle \left| F(t,U_1,V_1)-F(t,U_2,V_2)\right| +\left| G(t,U_1,V_1)-G(t,U_2,V_2)\right| \\ \displaystyle =\left| J_u(t,u^{*})\left( U_1-U_2\right) -\kappa \left( (1-\gamma w_{*})\dfrac{k}{(k+u^{*})^2}-\dfrac{k^{\prime }}{(k^{\prime }+v^{*})^2}\left( V_1-V_2\right) \right) \right| \\ \displaystyle \quad +\dfrac{1}{\epsilon }\left| F(V_1-V_2)+ \kappa \left( (1-\gamma w_{*})\dfrac{k}{(k+u^{*})^2}-\dfrac{k^{\prime }}{(k^{\prime }+v^{*})^2}\left( V_1-V_2\right) \right) \right| \\ \displaystyle \le \left( \left| \left| J_u\right| \right| _{\infty }+ \left( \kappa +\dfrac{\kappa }{\epsilon }\right) \right) \left| U_1-U_2\right| + \left( \kappa +\dfrac{\kappa }{\epsilon }\right) \left| V_1-V_2\right| \\ \displaystyle \le \left( \left| \left| J_u\right| \right| _{\infty }+ \left( \kappa +\dfrac{\kappa }{\epsilon }\right) \right) \left| \left| U_1-U_2,V_1-V_2\right| \right| , \end{array} \end{aligned}$$

which yields that H is Lipchitz with respect to X, and therefore, System (4.1)–(4.3) admits a unique solution $(U,V)\in C^1([0,T],\mathbb {R}_+)^2$ (see [8]). $\square$

Proof of Theorem 5.1

Proof

The remainders $\rho _h$ and $\theta _h$ satisfy

$$\begin{aligned} \begin{array}{llll} \displaystyle \rho ^{\prime } = J(t,u_h)-J(t,u_{*}) -J_uU -\kappa \left( (1-\gamma w_{*})\left( \dfrac{u_h}{k+u_h} -\dfrac{u_{*}}{k +u_{*}} -\dfrac{k}{(k +u_{*})^2}U\right) \right) \\ \displaystyle \hspace{0.5cm} +\kappa \left( \dfrac{v_h}{k^{\prime }+v_h} -\dfrac{v_{*}}{k^{\prime } +v_{*}} -\dfrac{k^{\prime }}{(k^{\prime } +v_{*})^2}V+ \gamma h\left( \dfrac{u_h}{k +u_h}-\dfrac{u_{*}}{k +u_{*}}\right) \right) \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{llll} \displaystyle \epsilon \theta _h^{\prime } =-F\theta _h +\kappa \left( (1-\gamma w_{*})\left( \dfrac{u_h}{k +u_h} -\dfrac{u_{*}}{k +u_{*}} -\dfrac{k}{(k +u_{*})^2}U\right) \right) \\ \displaystyle \hspace{0.5cm}-\kappa \left( \left( \dfrac{v_h}{k^{\prime } +v_h} -\dfrac{v_{*}}{k^{\prime } +v_{*}} -\dfrac{k^{\prime }}{(k^{\prime } +v_{*})^2}V\right) -\gamma h \left( \dfrac{u_h}{k +u_h}-\dfrac{u_{*}}{k +u_{*}}\right) \right) . \end{array} \end{aligned}$$

Setting $f(u) =\dfrac{k}{k +u}$ and $g(v) =\dfrac{k^{\prime }}{k^{\prime }+v}$, Taylor with integral remainder gives

$$\begin{aligned} f(u_h) -f(u_{*}) -f^{\prime }(u_{*})U =f^{\prime }(u_{*})\rho +\left( u_h -u_{*}\right) ^2\int _0^1 f^{\prime \prime }\left( zu_h +(1 -z)u_{*}\right) \left( 1-z\right) dz \end{aligned}$$

and

$$\begin{aligned} g(v_h) -g(v_{*}) -g^{\prime }(v_{*})V =g^{\prime }(v_{*})\theta +\left( v_h -v_{*}\right) ^2\int _0^1 g^{\prime \prime }\left( zv_h +(1 -z)v_{*}\right) \left( 1-z\right) dz. \end{aligned}$$

However, the remainders

$$\begin{aligned} R_1:=\int _0^1 f^{\prime \prime }\left( zu_h +(1 -z)u_{*}\right) \left( 1-z\right) dz \quad \text{ and }\quad R_2:= \int _0^1 g^{\prime \prime }\left( zv_h +(1 -z)v_{*}\right) \left( 1-z\right) dz, \end{aligned}$$

are bounded, so that

$$\begin{aligned} \left\Vert R_1\right\Vert _{\infty }\le c_{R_1} \quad \text{ and } \quad \left\Vert R_2\right\Vert _{\infty }\le c_{R_2} . \end{aligned}$$

Thus, $\rho$ satisfies

$$\begin{aligned} \begin{array}{lll} \displaystyle \rho ^{\prime }_h =J_u(t,u_{*})\rho _h +(u_h -u_{*})^2R_1 -\kappa \left( (1-\gamma w_{*})\left( f^{\prime }(u_{*})\rho _h +(u_h -u_{*})^2R_1\right) \right) \\ \displaystyle \hspace{0.5cm} +\kappa \left( g^{\prime }(v_{*})\theta _h +(v_h -v_{*})^2R_2 +\gamma h\left( f(u_h)-f(u_{*})\right) \right) . \end{array} \end{aligned}$$

Equivalently, we have

$$\begin{aligned} \begin{array}{lll} \displaystyle \rho ^{\prime }_h =J_u(t,u_{*})\rho _h +(u_h -u_{*})^2R_1 -\kappa \left( (1-\gamma w_{*})\left( f^{\prime }(u_{*})\rho _h +(u_h -u_{*})^2R_1\right) \right) \\ \displaystyle \hspace{0.5cm} +\kappa \left( g^{\prime }(v_{*})\theta _h +(v_h -v_{*})^2R_2 +\gamma h\left( f^{\prime }(u_{*})\left( u_h -u_{*}\right) \right) +(u_h -u_{*})^2R_1\right) \end{array} \end{aligned}$$

(A.10)

and $\theta$ satisfies

$$\begin{aligned} \begin{array}{lll} \epsilon \theta ^{\prime }_h = -F\theta _h +\kappa (1-\gamma w_{*})\left( f^{\prime }(u_{*})\rho _h +\left( u_h -u_{*}\right) ^2R_1\right) \\ \displaystyle \hspace{0.5cm} -\kappa \left( g^{\prime }(v_{*})\theta _h +(v_h -v_{*})^2R_2 +\gamma h\left( f(u_h)-f(u_{*})\right) \right) . \end{array} \end{aligned}$$

which is equivalent to

$$\begin{aligned} \epsilon \theta ^{\prime }_h= & {} -F\theta _h +\kappa (1-\gamma w_{*})\left( f^{\prime }(u_{*})\rho _h +\left( u_h -u_{*}\right) ^2R_1\right) -\kappa \left( g^{\prime }(v_{*})\theta _h \right. \nonumber \\{} & {} \left. +(v_h -v_{*})^2R_2 +\gamma h\left( f^{\prime }(u_{*})(u_h -u_{*}) +\left( u_h -u_{*}\right) ^2R_1\right) \right) . \end{aligned}$$

(A.11)

We need to prove some estimates.

Estimate 1. Multiplying (A.10) by $\rho _h$ and (A.11) by $\theta _h$, we find

$$\begin{aligned} ((\rho _h^{\prime }, \rho _h))&= ((J_u(t,u_{*})\rho _h,\rho _h)) +(((u_h -u_{*})^2R_1,\rho _h)) -\kappa (((1-\gamma w_{*})\\&\quad \times f^{\prime }(u_{*})\rho _h,\rho _h)) -\kappa (((1-\gamma w_{*})(u_h -u_{*})^2R_1,\rho _h))\\&\quad +\kappa ((g^{\prime }(v_{*})\theta _h,\rho _h)) +\kappa (((v_h -v_{*})^2R_2,\rho _h))\\&\quad +\kappa ((\gamma hf^{\prime }(u_{*})(u_h-u_{*}),\rho _h)) +\kappa ((h(u_h-u_{*})^2R_1,\rho _h))\\ \end{aligned}$$

and

$$\begin{aligned} ((\epsilon \theta ^{\prime }_h,\theta _h))&=-((F\theta _h,\theta _h)) +\kappa (((1-\gamma w_{*})f^{\prime }(u_{*})\rho _h,\theta _h)) \\&\quad +\kappa (((1-\gamma w_{*})(u_h -u_{*})^2R_1,\theta _h))-\kappa ((g^{\prime }(v_{*})\theta _h,\theta _h)) \\&\quad -\kappa (((v_h-v_{*})^2R_2,\theta _h))-\kappa ((\gamma h f^{\prime }(u_{*})(u_h -u_{*}),\theta _h)) \\&\quad -\kappa ((\gamma h(u_h-u_{*})^2R_1,\theta _h)). \end{aligned}$$

Consequently, after using Assumptions (E) and (F), and Cauchy–Schwarz inequality, we get

$$\begin{aligned} \begin{array}{llll} \displaystyle \dfrac{\textrm{d}}{\textrm{d}t}\left\Vert \rho _h\right\Vert ^2 \lesssim \left\Vert \rho _h\right\Vert ^2 +\left\Vert u_h -u_{*}\right\Vert ^2\left\Vert \rho _h\right\Vert +\left\Vert \theta _h\right\Vert \left\Vert \rho _h\right\Vert \\ \displaystyle \hspace{2cm} +c\left\Vert v_h -v_{*}\right\Vert ^2\left\Vert \rho _h\right\Vert +\left\Vert h\right\Vert \left\Vert u_h -u_{*}\right\Vert \left\Vert \rho _h\right\Vert \\ \displaystyle \hspace{2cm} +\left\Vert h(u_h-u_{*})^2\right\Vert \left\Vert \rho _h\right\Vert \end{array} \end{aligned}$$

(A.12)

and

$$\begin{aligned} \begin{array}{llll} \displaystyle \epsilon \dfrac{\textrm{d}}{\textrm{d}}\left\Vert \theta _h\right\Vert ^2 \lesssim \left\Vert \theta _h\right\Vert ^2 +\left\Vert \rho _h\right\Vert \left\Vert \theta _h\right\Vert +\left\Vert u_h -u_{*}\right\Vert ^2\left\Vert \theta _h\right\Vert \\ \displaystyle \hspace{2cm}+\left\Vert v_h -v_{*}\right\Vert ^2\left\Vert \theta _h\right\Vert +\left\Vert h\right\Vert \left\Vert u_h-u_{*}\right\Vert \left\Vert \theta _h\right\Vert \\ \displaystyle \hspace{2cm} +\left\Vert h(u_h-u_{*})^2\right\Vert \left\Vert \theta _h\right\Vert . \end{array} \end{aligned}$$

(A.13)

Combining (A.12) and (A.13), integrating over [0, t], and using Holder’s inequality, we get

$$\begin{aligned}{} & {} \displaystyle \left\Vert \rho _h(t)\right\Vert ^2 +\epsilon \left\Vert \theta _h(t)\right\Vert ^2 \lesssim \left\Vert \rho _h\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}\\{} & {} +\left\Vert \theta _h(s)\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)} +\left\Vert \theta _h\right\Vert _{L^2(0,t;\mathbb {R}_+)}\left\Vert \rho \right\Vert _{L^2(0,t;\mathbb {R}_+)} \\{} & {} +\left\Vert u_h -u_{*}\right\Vert _{L^{\infty }(0,t;\mathbb {R}_+)}\left\Vert u_h-u_{*}\right\Vert _{L^2(0,t;\mathbb {R}_+)}\left( \left\Vert \rho _h\right\Vert _{L^2(0,t;\mathbb {R}_+)} +\left\Vert \theta _h\right\Vert _{L^2(0,t;\mathbb {R}_+)}\right) \\{} & {} +\left\Vert v_h -v_{*}\right\Vert _{L^{\infty }(0,t;\mathbb {R}_+)}\left\Vert v_h -v_{*}\right\Vert _{L^2(0,t;\mathbb {R}_+)}\left( \left\Vert \rho _h\right\Vert _{L^2(0,t;\mathbb {R}_+)} +\left\Vert \theta _h\right\Vert _{L^2(0,t;\mathbb {R}_+)}\right) \\{} & {} +\left\Vert h\right\Vert _{L^2(0,t;\mathbb {R}_+)}\left\Vert u_h-u_{*}\right\Vert _{L^{\infty }(0,t;\mathbb {R}_+)}\left( \left\Vert \rho _h\right\Vert _{L^2(0,t;\mathbb {R}_+)} +\left\Vert \theta _h\right\Vert _{L^2(0,t;\mathbb {R}_+)}\right) \\{} & {} +\left\Vert h\right\Vert _{L^2(0,t;\mathbb {R}_+)}\left\Vert u_h-u_{*}\right\Vert ^2_{L^{\infty }(0,t;\mathbb {R}_+)}\left( \left\Vert \rho _h\right\Vert _{L^2(0,t;\mathbb {R}_+)} +\left\Vert \theta _h\right\Vert _{L^2(0,t;\mathbb {R}_+)}\right) .\\ \end{aligned}$$

Consequently, using Young’s inequality, Assumption (F), Equations (A.5), (A.6), and (A.7), we have

$$\begin{aligned} \begin{array}{llll} \displaystyle \left\Vert \rho _h(t)\right\Vert ^2 +\epsilon \left\Vert \theta _h(t)\right\Vert ^2 \lesssim c\left\Vert \rho _h\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}+ \left\Vert \theta _h\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}\\ \displaystyle \hspace{2cm}+c\left\Vert h\right\Vert ^4_{L^2(0,t;\mathbb {R}_+)} +\left\Vert h\right\Vert ^6_{L^2(0,t;\mathbb {R}_+)}\\ \displaystyle \hspace{2cm}\lesssim \left\Vert h\right\Vert ^4_{L^2(0,t;\mathbb {R}_+)}. \end{array} \end{aligned}$$

(A.14)

Estimate 2. Multiplying (A.10) by $\rho ^{\prime }_h$, and (A.11) by $\theta ^{\prime }_h$, we find

$$\begin{aligned} \displaystyle ((\rho _h^{\prime }, \rho _h^{\prime }))= & {} ((J_u(t,u_{*})\rho _h,\rho _h^{\prime })) +(((u_h -u_{*})^2R_1,\rho _h^{\prime })) \\{} & {} -\kappa (((1-\gamma w_{*})f^{\prime }(u_{*})\rho _h,\rho _h^{\prime }))-\kappa (((1-\gamma w_{*})(u_h -u_{*})^2R_1,\rho _h^{\prime }))\\{} & {} +\kappa ((g^{\prime }(v_{*})\theta _h,\rho _h^{\prime })) +\kappa (((v_h -v_{*})^2R_2,\rho _h^{\prime }))\\{} & {} \displaystyle +\kappa ((\gamma hf^{\prime }(u_{*})(u_h-u_{*}),\rho _h^{\prime })) +\kappa ((h(u_h-u_{*})^2R_1,\rho _h^{\prime })) \end{aligned}$$

and

$$\begin{aligned} \displaystyle ((\epsilon \theta ^{\prime }_h,\theta ^{\prime }_h))= & {} -((F\theta _h,\theta ^{\prime }_h)) +\kappa (((1-\gamma w_{*})f^{\prime }(u_{*})\rho _h,\theta ^{\prime }_h)) \\{} & {} +\kappa (((1-\gamma w_{*})(u_h -u_{*})^2R_1,\theta ^{\prime }_h))\\{} & {} -\kappa ((g^{\prime }(v_{*})\theta _h,\theta ^{\prime }_h)) -\kappa (((v_h-v_{*})^2R_2,\theta ^{\prime }_h)) \\{} & {} -\kappa ((\gamma h f^{\prime }(u_{*})(u_h -u_{*}),\theta ^{\prime }_h)) -\kappa ((\gamma h(u_h-u_{*})^2R_1,\theta ^{\prime }_h)). \end{aligned}$$

Then, using Cauchy–Schwarz inequality, we get

$$\begin{aligned} \displaystyle \left\Vert \rho _h^{\prime }\right\Vert ^2\lesssim & {} \displaystyle \dfrac{\textrm{d}}{\textrm{d}t}\left\Vert \rho _h\right\Vert ^2 +\left\Vert \theta _h\right\Vert \left\Vert \rho _h^{\prime }\right\Vert +\left\Vert u_h -u_{*}\right\Vert ^2\left\Vert \rho _h^{\prime }\right\Vert +\left\Vert v_h -v_{*}\right\Vert ^2\left\Vert \rho _h^{\prime }\right\Vert \nonumber \\{} & {} + \left\Vert h\right\Vert \left\Vert u_h -u_{*}\right\Vert \left\Vert \rho _h^{\prime }\right\Vert +\left\Vert h\right\Vert \left\Vert u_h -u_{*}\right\Vert ^2\left\Vert \rho _h^{\prime }\right\Vert \end{aligned}$$

(A.15)

and

$$\begin{aligned} \displaystyle \epsilon \left\Vert \theta _h^{\prime }\right\Vert ^2\lesssim & {} \displaystyle \dfrac{\textrm{d}}{\textrm{d}t}\left\Vert \theta _h\right\Vert ^2 +\left\Vert \rho _h\right\Vert \left\Vert \theta _h^{\prime }\right\Vert +\left\Vert u_h -u_{*}\right\Vert ^2\left\Vert \theta _h^{\prime }\right\Vert +\left\Vert v_h -v_{*}\right\Vert ^2\left\Vert \theta _h^{\prime }\right\Vert \nonumber \\{} & {} + \left\Vert h\right\Vert \left\Vert u_h -u_{*}\right\Vert \left\Vert \theta _h^{\prime }\right\Vert +\left\Vert h\right\Vert \left\Vert u_h -u_{*}\right\Vert ^2\left\Vert \theta _h^{\prime }\right\Vert . \end{aligned}$$

(A.16)

Combining (A.15) and (A.16), and integrating over [0, t], in addition to that, using Assumption (F) and Young’s inequality, we have

$$\begin{aligned}{} & {} \left\Vert \rho _h^{\prime }\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)} +\epsilon \left\Vert \theta _h^{\prime }\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}\lesssim \displaystyle \left\Vert \rho _h(t)\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)} \\{} & {} +\left\Vert \theta _h(t)\right\Vert ^2 +\left\Vert \theta _h\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)} +\left\Vert \rho _h\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)} \\{} & {} +\left\Vert u_h -u_{*}\right\Vert ^2_{L^{\infty }(0,t;\mathbb {R}_+)}\left\Vert u_h -u_{*}\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)} \\{} & {} +\left\Vert v_h -v_{*}\right\Vert ^2_{L^{\infty }(0,t;\mathbb {R}_+)}\left\Vert v_h -v_{*}\right\Vert ^2_{L^{2}(0,t;\mathbb {R}_+)} \\{} & {} +\left\Vert h\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}\left\Vert u_h -u_{*}\right\Vert ^2_{L^{\infty }(0,t;\mathbb {R}_+)} +\left\Vert h\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}\left\Vert u_h -u_{*}\right\Vert ^4_{L^{\infty }(0,t;\mathbb {R}_+)}. \end{aligned}$$

Further, using Equations (A.14), (A.5), (A.6), and (A.7), we infer

$$\begin{aligned} \begin{array}{llll} \displaystyle \left\Vert \rho _h^{\prime }\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)} +\epsilon \left\Vert \theta _h^{\prime }\right\Vert ^2_{L^2(0,t;\mathbb {R}_+)}\lesssim \left\Vert h\right\Vert ^4_{L^2(0,t;\mathbb {R}_+)}, \end{array} \end{aligned}$$

and hence the result. $\square$