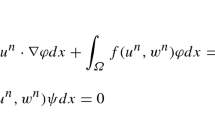Skip to main content
Springer Nature Link
Log in

Optimality Conditions for Optimal Control of the Monodomain Model with Pointwise Control and State Constraints

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

This work deals with the theoretical study of the optimality conditions for the optimal control of the monodomain model arising in cardiac electrophysiology with mixed control-state constraints. The monodomain model is a coupled system of reaction–diffusion equation with cubic nonlinearity in the reaction term and an ordinary differential equation. The existence of optimal control is established, and the twice Fréchet differentiability of the control-to-state operator is discussed. The first-order necessary optimality condition is derived. Most significantly, a detailed proof of the sufficient second-order optimality condition is demonstrated with mixed control-state constraints.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Availability of data and materials

Not applicable.

References

  1. Bonnans, J.F.: Second-order analysis for control constrained optimal control problem. Appl. Math. Optim. 38, 303–325 (1998)

    Article  MathSciNet  Google Scholar 

  2. Boulakia, M., Fernández, M.A., Gerbeau, J.F., Zemzemi, N.: A coupled system of PDEs and ODEs arising in electrocardiograms modeling. Appl. Math. Res. Express. abn0022, 1–28 (2008)

    Google Scholar 

  3. Bourgault, Y., Coudiere, Y., Pierre, C.: Existence and uniqueness of the solution for the bidomain model used in cardiac electrophysiology. Nonlinear Anal. Real World Appl. 10, 458–482 (2009)

    Article  MathSciNet  Google Scholar 

  4. Brandao, A.J., Fernandez-Cara, E., Magalhaes, P., Rojas-Medar, M.A.: Theoretical analysis and control results for the FitzHugh-Nagumo equation. Electron. J. Differ. Equ. 164, 1–20 (2008)

    MathSciNet  Google Scholar 

  5. Casas, E.: Pontryagin’s principle for state-constrained boundary control problems of semilinear parabolic equations. SIAM J. Control. Optim. 35, 1297–1327 (1997)

    Article  MathSciNet  Google Scholar 

  6. Casas, E., Reyes, J.C., Tröltzsch, F.: Sufficient second-order optimality conditions for semilinear control problems with pointwise state constraints. SIAM J. Optim. 19, 616–643 (2008)

    Article  MathSciNet  Google Scholar 

  7. Casas, E., Ryll, C., Tröltzsch, F.: Sparse optimal control of the Schlögl and FitzHugh-Nagumo systems. J. Comput. Appl. Math. 13, 415–442 (2013)

    Google Scholar 

  8. Casas, E., Tröltzsch, F.: Second-order necessary and sufficient optimality conditions for optimization problems and applications to control theory. SIAM J. Optim. 13, 406–431 (2002)

    Article  MathSciNet  Google Scholar 

  9. Casas, E., Tröltzsch, F., Unger, A.: Second order sufficient optimality conditions for some state-constrained control problems of semilinear elliptic equations. SIAM J. Control. Optim. 38, 1369–1391 (2000)

    Article  MathSciNet  Google Scholar 

  10. Casas, E.: Boundary control of semilinear elliptic equations with pointwise state constraints. SIAM J. Control. Optim. 31, 993–1006 (1993)

    Article  MathSciNet  Google Scholar 

  11. Casas, E., Tröltzsch, F.: Second order analysis for optimal control problems: improving results expected from abstract theory. SIAM J. Optim. 22, 261–279 (2012)

    Article  MathSciNet  Google Scholar 

  12. Chamakuri, N., Kunisch, K.: Primal-dual active set strategy for large scale optimization of cardiac defibrillation. Appl. Math. Comput. 292, 178–193 (2017)

    Article  MathSciNet  Google Scholar 

  13. Chamakuri, N., Kunisch, K., Plank, G.: Numerical solution for optimal control of the reaction-diffusion equations in cardiac electrophysiology. Comput. Optim. Appl. 49, 149–178 (2011)

    Article  MathSciNet  Google Scholar 

  14. Hehl, A., Neitzel, I.: Second-order optimality conditions for an optimal control problem governed by a regularized phase-field fracture propagation model. Optimization 72, 1665–1689 (2023)

    Article  MathSciNet  Google Scholar 

  15. Hoppe, F., Neitzel, I.: Optimal control of quasilinear parabolic PDEs with state-constraints. SIAM J. Control. Optim. 60, 330–354 (2022)

    Article  MathSciNet  Google Scholar 

  16. Krumbiegel, K., Rehberg, J.: Second order sufficient optimality conditions for parabolic optimal control problems with pointwise state constraints. SIAM J. Control. Optim. 51, 304–331 (2013)

    Article  MathSciNet  Google Scholar 

  17. Kunisch, K., Wagner, M.: Optimal control of the bidomain system (I): The monodomain approximation with the Rogers-McCulloch model. Nonlinear Anal. Real World Appl. 13, 525–1550 (2012)

    Article  MathSciNet  Google Scholar 

  18. Malanowski, K.: Sufficient optimality conditions for optimal control subject to state constraints. SIAM J. Control. Optim. 35, 205–227 (1997)

    Article  MathSciNet  Google Scholar 

  19. Maurer, H.: First and second order sufficient optimality conditions in mathematical programming and optimal control. In: König, H., Korte, B., Ritter, K. (eds.) Mathematical Programming at Oberwolfach, vol. 1, pp. 163–177. Springer, Berlin, Heidelberg (1981)

    Chapter  Google Scholar 

  20. Maurer, H., Zowe, J.: First and second-order necessary and sufficient optimality conditions for infinite-dimensional programming problems. Math. Program. 16, 98–110 (1979)

    Article  MathSciNet  Google Scholar 

  21. Raviart, P. A., Thomas, J. M.: Introduction à l’analyse numérique des équations aux dérivées partielles, Elsevier Masson (1983)

  22. Raymond, J.P., Tröltzsch, F.: Second order sufficient optimality conditions for nonlinear parabolic control problems with state constraints. Discrete Contin. Dyn. Syst. 6, 431–450 (2000)

    Article  MathSciNet  Google Scholar 

  23. Rogers, J.M., McCulloch, A.D.: A collocation-Galerkin finite element model of cardiac action potential. IEEE Trans. Biomed. Eng. 41, 743–757 (1994)

    Article  Google Scholar 

  24. Rösch, A., Tröltzsch, F.: Sufficient second-order optimality conditions for a parabolic optimal control problem with pointwise control-state constraints. SIAM J. Control. Optim. 42, 138–154 (2003)

    Article  MathSciNet  Google Scholar 

  25. Serovajsky, S.: State-constrained optimal control of nonlinear elliptic variational inequalities. Optim. Lett. 8, 2041–2051 (2014)

    Article  MathSciNet  Google Scholar 

  26. Silva, F.J.: Second order analysis for the optimal control of parabolic equations under control and final state constraints. Set-Valued Var. Anal. 24, 57–81 (2016)

    Article  MathSciNet  Google Scholar 

  27. Thuy, L.Q., Toan, N.T.: Second-order sufficient optimality conditions for an optimal control problem with mixed constraints. Results Math. 77, 208–242 (2022)

    Article  MathSciNet  Google Scholar 

  28. Tröltzsch, F.: Optimal control of partial differential equations: Theory, Methods, and Applications, American Mathematical Soc. (2010)

Download references

Acknowledgements

MR thanks CSIR, India (09/874(0042)/2021-EMR-I), SKN acknowledges Science and Engineering Research Board, SERB-MATRICS, India (MTR/2023/000637), and NC acknowledges SERB, Department of Science and Technology, India (CRG/2022/006421), for their financial support. Also, we express our gratitude to the anonymous reviewers for their constructive comments and insightful suggestions, which have greatly contributed to enhancing the content of the paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology Calicut, Kozhikode, India

    Maria Robert & Suresh Kumar Nadupuri

  2. School of Mathematics, IISER Thiruvananthapuram, Thiruvananthapuram, India

    Nagaiah Chamakuri

  3. Center for High-Performance Computing, IISER Thiruvananthapuram, Thiruvananthapuram, India

    Nagaiah Chamakuri

Authors
  1. Maria Robert
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Suresh Kumar Nadupuri
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Nagaiah Chamakuri
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Suresh Kumar Nadupuri.

Ethics declarations

Conflict of interest

The authors declare that there is no Conflict of interest.

Additional information

Communicated by Nikolai Osmolovski.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Robert, M., Nadupuri, S.K. & Chamakuri, N. Optimality Conditions for Optimal Control of the Monodomain Model with Pointwise Control and State Constraints. J Optim Theory Appl 202, 605–627 (2024). https://doi.org/10.1007/s10957-024-02440-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-024-02440-3

Keywords