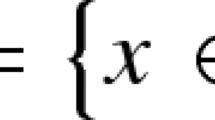Skip to main content
Springer Nature Link
Log in

On Quasiconvex Multiobjective Optimization and Variational Inequalities Using Greenberg–Pierskalla Based Generalized Subdifferentials

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

In this paper, we first characterize generalized convex functions introduced by Linh and Penot Optimization (62: 943–959, 2013) by using generalized monotonicity of the generalized subdifferentials. We use vector variational inequalities in terms of generalized subdifferentials to identify efficient solutions of a multiobjective optimization problem involving quasiconvex functions. We also establish the Minty variational principle by utilizing the mean value theorem established by Kabgani and Soleimani-damaneh (Numer. Funct. Anal. Optim 38: 1548–1563, 2017) for quasiconvex functions in terms of Greenberg–Pierskalla subdifferentials.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data Availability

Data sharing was not applicable to this article as no data sets were generated or analysed during the current study.

References

  1. Al-Homidan, S., Ansari, Q.H.: Generalized Minty vector variational-like inequalities and vector optimization problems. J. Optim. Theory Appl. 144, 1–11 (2010). https://doi.org/10.1007/s10957-009-9591-7

    Article  MathSciNet  Google Scholar 

  2. Aussel, D., Corvellec, J.N., Lassonde, M.: Subdifferential characterization of quasiconvexity and convexity. J. Convex Anal. 1(2), 195–201 (1994)

    MathSciNet  Google Scholar 

  3. Ansari, Q.H., Lee, G.M.: Nonsmooth vector optimization problems and Minty vector variational inequalities. J. Otim. Theory Appl. 145, 1–16 (2010). https://doi.org/10.1007/s10957-009-9638-9

    Article  MathSciNet  Google Scholar 

  4. Ansari, Q.H.: On generalized vector variational-like inequalities. Ann. Sci. Math. Qué 19(2), 131–137 (1995)

    MathSciNet  Google Scholar 

  5. Ansari Ardali, A., Movahedian, N., Nobakhtian, S.: Optimality conditions for nonsmooth mathematical programs with equilibrium constraints, using convexificators. Optimization 65(1), 67–85 (2016). https://doi.org/10.1080/02331934.2014.987776

    Article  MathSciNet  Google Scholar 

  6. Ansari, Q.H., Rezaie, M., Zafarani, J.: Generalized vector variational-like inequalities and vector optimization. J. Glob. Optim. 53, 271–284 (2012). https://doi.org/10.1007/s10898-011-9686-1

    Article  MathSciNet  Google Scholar 

  7. Ansari, Q.H., Rezaie, M.: Generalized vector variational-like inequalities and vector optimization in Asplund spaces. Optimization 62, 721–734 (2013). https://doi.org/10.1080/02331934.2012.669758

    Article  MathSciNet  Google Scholar 

  8. Al-Homidan, S., Ansari, Q.H.: Generalized Minty vector variational-like inequalities and vector optimization problems. J. Optim. Theory Appl. 144, 1–11 (2010). https://doi.org/10.1007/s10957-009-9591-7

    Article  MathSciNet  Google Scholar 

  9. Clarke, F.H., Ledyaev, Y.S., Stern, R.J., Wolenski, P.R.: Nonsmooth Analysis and Control Theory. Springer, New York (1998)

    Google Scholar 

  10. Crouzeix, J.P., Legaz, J.E.M., Volle, M. (eds.): Generalized Convexity, Generalized Monotonicity: Recent Results, vol. 27. Springer, Cham (2013)

    Google Scholar 

  11. Fan, L., Liu, S., Gao, S.: Generalized monotonicity and convexity of non-differentiable functions. J. Math. Anal. Appl. 279(1), 276–289 (2003)

    Article  MathSciNet  Google Scholar 

  12. Gang, X., Liu, S.: On Minty vector variational-like inequality. Comput. Math. Appl. 56, 311–323 (2008). https://doi.org/10.1016/j.camwa.2007.12.011

    Article  MathSciNet  Google Scholar 

  13. Giannessi, F.: Theorems of alternative, quadratic programs and complementarity problems. In: Cottle, R.W., Giannessi, F., Lions, J.L. (eds.) Variational Inequality and complementarity problems, pp. 151–186. Wiley, New York (1980)

    Google Scholar 

  14. Giannessi, F.: On Minty Variational Principle. In: Giannessi, F., Komlósi, S., Rapcsáck, T. (eds.) New Trends in Mathematical Programming, Applied Optimization, pp. 93–99. Springer, Boston (1998)

    Chapter  Google Scholar 

  15. Golestani, M., Nobakhtian, S.: Convexificators and strong Kuhn–Tucker conditions. Comput. Math. Appl. 64(4), 550–557 (2012). https://doi.org/10.1016/j.camwa.2011.12.047

    Article  MathSciNet  Google Scholar 

  16. Greenberg, H.J., Pierskalla, W.P.: Quasiconjugate functions and surrogate duality. Cahiers Centre études Rech. Opér. 15, 437–448 (1973)

    MathSciNet  Google Scholar 

  17. Hartman, P., Stampacchia, G.: On some nonlinear elliptic differential functional equations. Acta Math. 115, 153–188 (1980)

    Google Scholar 

  18. Hadjisavvas, N., Komlósi, S., Schaible, S.S.: Handbook of Generalized Cnvexity and Gneralized Monotonicity, vol. 76. Springer, Cham (2006)

    Google Scholar 

  19. Jeyakumar, V., Luc, D.T.: Nonsmooth calculus, minimality, and monotonicity of convexificators. J. Optim. Theory Appl. 101, 599–621 (1999)

    Article  MathSciNet  Google Scholar 

  20. Jaisawal, P., Laha, V.: On sufficiency and duality for multiobjective programming problems using convexificators. Filomat 36(9), 3119–3139 (2022)

    Article  MathSciNet  Google Scholar 

  21. Kabgani, A., Soleimani-damaneh, M.: Relationships between convexificators and Greenberg–Pierskalla subdifferentials for quasiconvex functions. Numer. Funct. Anal. Optim. 38(12), 1548–1563 (2017). https://doi.org/10.1080/01630563.2017.1349144

    Article  MathSciNet  Google Scholar 

  22. Komlósi, S.: On the Stampacchia and Minty variational inequalities. In: Giorgi, G., Rossi, F. (eds.) Generalized convexity and optimization for economic and financial decisions, pp. 231–260. Pitagora Editrice, Bologna (1999)

    Google Scholar 

  23. Luc, D.-T.: Characterisations of quasiconvex functions. Bull. Austral. Math. Soc. 48, 393–406 (1993)

    Article  MathSciNet  Google Scholar 

  24. Laha, V., Mishra, S.K.: On vector optimization problems and vector variational inequalities using convexificators. Optimization 66(11), 1837–1850 (2017). https://doi.org/10.1080/02331934.2016.1250268

    Article  MathSciNet  Google Scholar 

  25. Laha, V., Al-Shamary, B., Mishra, S.K.: On nonsmooth \(V-\)invexity and vector variational-like inequalities in terms of the Michel–Penot subdifferentials. Optim. Lett. 8, 1675–1690 (2014). https://doi.org/10.1007/s11590-013-0707-5

    Article  MathSciNet  Google Scholar 

  26. Laha, V., Singh, H.N.: On multiobjective optimization problems involving \(V-r-\)invexity. Commun. Appl. Nonlinear Anal. 26(1), 76–85 (2019)

    MathSciNet  Google Scholar 

  27. Laha, V., Dwivedi, A.: On approximate strong KKT points of nonsmooth interval-valued mutiobjective optimization problems using convexificators. J. Anal. 32(1), 219–242 (2024)

    Article  MathSciNet  Google Scholar 

  28. Linh, N.T.H., Penot, J.P.: Generalized convex functions and generalized differentials. Optimization 62(7), 943–959 (2013). https://doi.org/10.1080/02331934.2011.611882

    Article  MathSciNet  Google Scholar 

  29. Minty, G.J.: On the generalization of a direct method of the calculus of variations. Bull. Am. Math. Soc. 73, 314–321 (1967)

    Article  MathSciNet  Google Scholar 

  30. Mishra, S.K., Laha, V.: On generalized Minty and Stampacchia vector variational-like inequalities and \(V-\)invex vector optimization in Asplund spaces. Adv. Nonlinear Var. Inequal. 16, 43–60 (2013)

    MathSciNet  Google Scholar 

  31. Mishra, S.K., Wang, S.Y.: Vector variational-like inequalities and non-smooth vector optimization problems. Nonlinear Anal. (2006). https://doi.org/10.1016/j.na.2005.07.030

    Article  MathSciNet  Google Scholar 

  32. Mishra, S.K., Wang, S.Y., Lai, K.K.: On non-smooth \(\alpha -\)invex functions and vector variational-like inequality. Optim. Lett. 2, 91–98 (2008). https://doi.org/10.1007/s11590-007-0045-6

    Article  MathSciNet  Google Scholar 

  33. Mishra, S.K., Laha, V.: On approximately star-shaped functions and approximate vector variational inequalities. J. Optim. Theory Appl. 156, 278–293 (2013). https://doi.org/10.1007/s10957-012-0124-4

    Article  MathSciNet  Google Scholar 

  34. Mishra, S.K., Kumar, R., Laha, V., Maurya, J.K.: Optimality and duality for semidefinite multiobjective programming problems using convexificators. J. Appl. Numer. Optim. 4(1), 103–118 (2022)

    Google Scholar 

  35. Mordukhovich, B.S.: Variational Analysis and Generalized Differentiation I. Springer, Berlin (2006)

    Book  Google Scholar 

  36. Mishra, S.K., Laha, V.: On \(V-r-\)invexity and vector variational-like inequalities. Filomat 26, 1065–1073 (2012). https://doi.org/10.2298/FIL1205065M

    Article  MathSciNet  Google Scholar 

  37. Mishra, S.K., Noor, M.A.: On vector variational-like inequality problems. J. Math. Anal. Appl. 311(1), 69–75 (2005). https://doi.org/10.1016/j.jmaa.2005.01.070

    Article  MathSciNet  Google Scholar 

  38. Pandey, Y., Mishra, S.K.: Optimality conditions and duality for semi-infinite mathematical programming problems with equilibrium constraints, using convexificators. Ann. Oper. Res. 269(1), 549–564 (2018). https://doi.org/10.1007/s10479-017-2422-6

    Article  MathSciNet  Google Scholar 

  39. Pandey, Y., Mishra, S.K.: Duality for nonsmooth optimization problems with equilibrium constraints, using convexificators. J. Optim. Theory Appl. 171(2), 694–707 (2016). https://doi.org/10.1007/s10957-016-0885-2

    Article  MathSciNet  Google Scholar 

  40. Penot, J.P.: Are generalized derivatives useful for generalized convex functions? In: Crouzeix, J.P., Martínez-Legaz, J.E., Volle, M. (eds.) Generalized Convexity, Generalized monotonicity: Recent Results, pp. 3–59. Springer, US (1998)

    Chapter  Google Scholar 

  41. Penot, J.P.: Glimpses upon quasiconvex analysis. In: ESAIM: Proceedings, vol 20, EDP Sciences, pp 170–194 (2007)

  42. Penot, J.P., Quang, P.H.: Generalized convexity of functions and generalized monotonicity of set-valued maps. J. Optim. Theory Appl. 92, 343–356 (1997)

    Article  MathSciNet  Google Scholar 

  43. Siddiqi, A.H., Ansari, Q.H., Ahmed, R.: On vector variational-like inequalities. Indian J. Pure Appl. Math. 28(8), 1009–1016 (1997)

    MathSciNet  Google Scholar 

  44. Singh, H.N., Laha, V.: On Minty variational principle for quasidifferentiable vector optimization problems. Optim. Methods Softw. 38(2), 243–261 (2023). https://doi.org/10.1080/10556788.2022.2119235

    Article  MathSciNet  Google Scholar 

  45. Stampacchia, G.: Formes bilineaires coercitives sur les ensembles convexes. C R. Acad. Sci. Paris 9, 4413–4416 (1960)

    MathSciNet  Google Scholar 

  46. Suzuki, S., Kuroiwa, D.: Characterizations of the solution set for quasiconvex programming in terms of Greenberg–Pierskalla subdifferential. J. Glob. Optim. 62, 431–441 (2015). https://doi.org/10.1007/s10898-014-0255-2

    Article  MathSciNet  Google Scholar 

  47. Yang, X.Q., Yang, X.M.: Vector variational-like inequality with pseudoinvexity. Optimization 55(1–2), 157–170 (2006). https://doi.org/10.1080/02331930500530609

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors are thankful to the editors and the anonymous referees for the careful reading of the paper and for the helpful constructive suggestions to improve the quality of the paper. The first author is financially supported by "Research Grant for Faculty" (IoE Scheme) under Dev. Scheme NO. 6031. The second author is supported by UGC-BSR start up grant by University Grant Commission, New Delhi, India (Letter No. F.30-370/2017(BSR)) (Project No. M-14-40). The third author is financially supported by CSIR-UGC JRF, New Delhi, India, through Reference no.: 1009/(CSIR-UGC NET JUNE 2018).

Author information

Authors and Affiliations

  1. Department of Mathematics, Institute of Science, Banaras Hindu University, Varanasi, Uttar Pradesh, 221005, India

    Shashi Kant Mishra & Vivek Laha

  2. Department of Mathematics, University of Ladakh, Leh Campus, Leh, UT Ladakh, India

    Mohd Hassan

Authors
  1. Shashi Kant Mishra
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Vivek Laha
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Mohd Hassan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Vivek Laha.

Additional information

Communicated by Xinmin Yang.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mishra, S.K., Laha, V. & Hassan, M. On Quasiconvex Multiobjective Optimization and Variational Inequalities Using Greenberg–Pierskalla Based Generalized Subdifferentials. J Optim Theory Appl 202, 1169–1186 (2024). https://doi.org/10.1007/s10957-024-02505-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-024-02505-3

Keywords

Mathematics Subject Classification