Relating instance hardness to classification performance in a dataset: a visual approach

Abstract

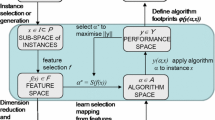
Machine Learning studies often involve a series of computational experiments in which the predictive performance of multiple models are compared across one or more datasets. The results obtained are usually summarized through average statistics, either in numeric tables or simple plots. Such approaches fail to reveal interesting subtleties about algorithmic performance, including which observations an algorithm may find easy or hard to classify, and also which observations within a dataset may present unique challenges. Recently, a methodology known as Instance Space Analysis was proposed for visualizing algorithm performance across different datasets. This methodology relates predictive performance to estimated instance hardness measures extracted from the datasets. However, the analysis considered an instance as being an entire classification dataset and the algorithm performance was reported for each dataset as an average error across all observations in the dataset. In this paper, we developed a more fine-grained analysis by adapting the ISA methodology. The adapted version of ISA allows the analysis of an individual classification dataset by a 2-D hardness embedding, which provides a visualization of the data according to the difficulty level of its individual observations. This allows deeper analyses of the relationships between instance hardness and predictive performance of classifiers. We also provide an open-access Python package named PyHard, which encapsulates the adapted ISA and provides an interactive visualization interface. We illustrate through case studies how our tool can provide insights about data quality and algorithm performance in the presence of challenges such as noisy and biased data.

Appendices

Appendix A Proof of proposition

Proposition 1

(cross-entropy bounds). For any classification problem with C classes there is a lower bound $L_{\mathrm {lower}}$ and an upper bound $L_{\mathrm {upper}}$ for the cross-entropy loss (aka log-loss) such that: if $\mathrm {logloss}({\mathbf {x}}_i) < L_{lower}$, the prediction was correct; if $\mathrm {logloss}({\mathbf {x}}_i) > L_{upper}$, the prediction was incorrect; and if $L_{\mathrm {lower}} \le {\mathrm {logloss}}({\mathbf {x}}_i) \le L_{\mathrm {upper}}$, the prediction can be either correct or incorrect , where ${\mathrm {logloss}}({\mathbf {x}}_i)$ is the log-loss of instance ${\mathbf {x}}_i$. Specifically, these bounds can be set as $L_{\mathrm {lower}}=-\log \big (\frac{1}{2}\big ){=\log 2}$ and $L_{\mathrm {upper}}=-\log \big (\frac{1}{C}\big )={\log C}$.

Proof

Given a multiclass setting consisting of C classes, the outcome of a classifier is the predicted probability vector $[p_1, p_2, \dots , p_{C}]$, and the predicted class is defined as $\mathop {\hbox {arg max}}\limits _j p_j$. And $y_{j, c} :=I_{j=c}$ indicates the true class c.

We first prove that if the classifier succeeds in correctly predicting the class of instance ${\mathbf {x}}_i$, then ${\mathrm {logloss}}({\mathbf {x}}_i) < L_{\mathrm {upper}}$ and that the value of $L_{\mathrm {upper}}$ is $-\log (\frac{1}{C})$. Without loss of generality, suppose $j=1$ is the correct class, since the classes can be always reordered so that each one of them becomes the first in the set. In that case, $\mathop {\hbox {arg max}}\limits _j p_j = 1$, which implies that:

$$\begin{aligned} p_1&> p_2\\ p_1&> p_3\\&\vdots \\ p_1&> p_{C} \end{aligned}$$

Summing all those inequalities results in

$$\begin{aligned} (C-1) p_1 > p_2 + \cdots + p_{C} \end{aligned}$$

On the other hand, $\sum _j p_j = 1$. Therefore,

$$\begin{aligned} (C-1) p_1&> 1 - p_1\\ p_1&> \frac{1}{C}\\ \log p_1&> \log \frac{1}{C}\\ - \log p_1&< - \log \frac{1}{C}\\ - y_{1, c} \log p_1&< - \log \frac{1}{C}\\ \therefore {\mathrm {logloss}}({\mathbf {x}}_i)&< - \log \frac{1}{C} = L_{\mathrm {upper}}\\ \end{aligned}$$

However, if ${\mathrm {logloss}}({\mathbf {x}}_i) < L_{\mathrm {upper}}$ it does not necessarily imply that the instance ${\mathbf {x}}_i$ was correctly classified. We show this by counterexample: take the particular predicted probability vector $\big [\frac{1}{2} - \varepsilon , \frac{1}{2} + \varepsilon , 0, \dots , 0\big ]$, and define the right class as $c=1$. For this vector, the classifier predicts the class 2, since it has the highest probability. The log-loss value is

$$\begin{aligned} -\sum _{j=1}^{C} y_{j, c} \log p_j = -y_{1, c} \log p_1 = -\log \Big (\frac{1}{2} - \varepsilon \Big ) \end{aligned}$$

If we choose $0< \varepsilon < \frac{1}{2} - \frac{1}{C}$, which is always possible for $C \ge 3$, then

$$\begin{aligned} {\mathrm {logloss}}({\mathbf {x}}_i)&= -\log \Big (\frac{1}{2} - \varepsilon \Big )\\&< -\log \Big (\frac{1}{2} - \frac{1}{2} + \frac{1}{C} \Big )\\&< -\log \frac{1}{C} = L_{\mathrm {upper}} \end{aligned}$$

Specifically for binary problems with only two classes, if ${\mathrm {logloss}}({\mathbf {x}}_i) < - \log \frac{1}{2}$, then

$$\begin{aligned} - y_{1, c} \log p_1 < - \log \frac{1}{2} \implies p_1> \frac{1}{2} > p_2 \implies \mathop {\hbox {arg max}}\limits _j p_j = 1 \end{aligned}$$

So, in the particular case of binary classification problems, $L_{\mathrm {lower}} = L_{\mathrm {upper}}$. Thus,

$$\begin{aligned} \mathop {\hbox {arg max}}\limits _j p_j = 1 \iff {\mathrm {logloss}}({\mathbf {x}}_i) < -\log \frac{1}{2} \quad (\text {binary class problems}) \end{aligned}$$

To find $L_{\mathrm {lower}}$, we first show that a multiclass problem can be reduced to a binary classification problem in the sense of log loss metric. Herewith, the vector $[p_1, p_2, \dots , p_n]$ is equivalent to $[p_1, p_2']$, with $p_2' = \sum _{j=2}^{C} p_j$. In both cases, the log loss value is the same. Thus, we assume $L_{\mathrm {lower}} = -\log \frac{1}{2}$ and prove it by contradiction.

Assume that ${\mathrm {logloss}}({\mathbf {x}}_i) < -\log \frac{1}{2}$, that the correct class is $c=1$ and $\exists p_k : p_k > p_1$ (classification error). Then,

$$\begin{aligned}&-\log p_1< -\log \frac{1}{2}\\&\implies \frac{1}{2}< p_1< p_k\\&\implies 1 < p_1 + p_k \quad (\mathrm {absurd!}) \end{aligned}$$

Therefore, $L_{\mathrm {lower}} = -\log \frac{1}{2}$. $\square$

Appendix B Additional figures

Additional figures from the analysis of the COMPAS dataset are presented here. They show the Lasso selections of easy and hard instances (Fig. 14) and distributions of some other attributes besides race, namely number of priors (Fig. 15a), age (Fig. 15b) and sex (Fig. 15c). Median values are represented by vertical dashed lines. A summary of these results is presented and discussed in Sect.  4.2 using Table 2.

Fig. 14

Lasso selection of hard and easy instances from the COMPAS dataset ISA projections with and without race as an attribute

Fig. 15

Distribution of different features values for the entire COMPAS dataset, low IH and high IH data points, with race as an input attribute