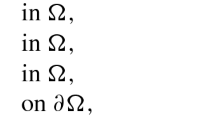Abstract
This paper is concerned with the existence of positive solutions for a class of quasilinear singular elliptic systems with Dirichlet boundary condition. By studying the competition between the Caffarelli–Kohn–Nirenberg exponents, the sign-changing potentials and the nonlinear terms, we establish an interval on the range of multiple parameters over which solutions exist in an appropriate weighted Sobolev space. The arguments rely on the method of weak sub- and super-solutions.
Similar content being viewed by others
References
G.A. Afrouzi, S.H. Rasouli, A remark on the existence of multiple solutions to a multiparameter nonlinear elliptic system. Nonlinear Anal. 71, 445–455 (2009)
N. Akhmediev, A. Ankiewicz, Partially coherent solitons on a finite background. Phys. Rev. Lett. 82, 2661–2664 (1999)
J. Ali, R. Shivaji, Positive solutions for a class of \( p \)-Laplacian systems with multiple parameters. J. Math. Anal. Appl. 335, 1013–1019 (2007)
J. Ali, R. Shivaji, M. Ramaswamy, Multiple positive solutions for classes of elliptic systems with combined nonlinear effects. Differ. Integral Equ. 19, 669–680 (2006)
C.O. Alves, D.G. de Figueiredo, Nonvariational elliptic systems. Discrete Contin. Dyn. Syst. 8, 289–302 (2002)
A. Ambrosetti, J.G. Azorero, I. Peral, Existence and multiplicity results for some nonlinear elliptic equations. Rend. Mat. Appl. 7, 167–198 (2000)
C. Atkinson, K. El Kalli, Some boundary value problems for the Bingham model. J. Non Newton. Fluid Mech. 41, 339–363 (1992)
H. Bueno, G. Ercole, W. Ferreira, A. Zumpano, Existence and multiplicity of positive solutions for the \(p\)-Laplacian with nonlocal coefficient. J. Math. Anal. Appl. 343, 151–158 (2008)
L. Caffarelli, R. Kohn, L. Nirenberg, First order interpolation inequalities with weights. Compos. Math. 53, 259–275 (1984)
A. Canada, P. Drábek, J.L. Gámez, Existence of positive solutions for some problems with nonlinear diffusion. Trans. Am. Math. Soc. 349, 4231–4249 (1997)
F. Catrina, Z.-Q. Wang, On the Caffarelli-Kohn-Nirenberg inequalities: sharp constants, existence (and nonexistence), and symmetry of extremal functions. Commun. Pure Appl. Math. 54, 229–258 (2001)
R. Dalmasso, Existence and uniqueness of positive solutions of semilinear elliptic systems. Nonlinear Anal. 39, 559–568 (2000)
E.N. Dancer, Competing species systems with diffusion and large interaction. Rend. Sem. Mat. Fis. Milano 65, 23–33 (1995)
R. Dautray, J.-L. Lions, Mathematical Analysis and Numerical Methods for Science and Technology, vol. 1: Physical Origins and Classical Methods (Springer, Berlin, Heidelberg, New York, 1985)
P. Drabek, J. Hernandez, Existence and uniqueness of positive solutions for some quasilinear elliptic problem. Nonlinear Anal. 44, 189–204 (2001)
J.F. Escobar, Uniqueness theorems on conformal deformations of metrics, Sobolev inequalities, and an eigenvalue estimate. Commun. Pure Appl. Math. 43, 857–883 (1990)
F. Fang, S. Liu, Nontrivial solutions of superlinear \(p\)-Laplacian equations. J. Math. Anal. Appl. 351, 3601–3619 (2009)
R. Filippucci, P. Pucci, V. Rădulescu, Existence and non-existence results for quasilinear elliptic exterior problems with nonlinear boundary conditions. Commun. Partial Differ. Equ. 33, 706–717 (2008)
D.D. Hai, R. Shivaji, An existence result on positive solutions for a class of semi-linear elliptic systems. Proc. R. Soc. Edinb. Sect. A 134, 137–141 (2004)
J.R. Graef, S. Heidarkhani, L. Kong, Multiple solutions for systems of multi-point boundary value problems. Opusc. Math. 33, 293–306 (2013)
D.D. Hai, R. Shivaji, An existence result on positive solutions for a class of \(p\)-Laplacian systems. Nonlinear Anal. 56, 1007–1010 (2004)
O.H. Miyagaki, R.S. Rodrigues, On positive solutions for a class of singular quasilinear elliptic systems. J. Math. Anal. Appl. 334, 818–833 (2007)
M.K.V. Murthy, G. Stampacchia, Boundary value problems for some degenerate elliptic operators. Ann. Mat. Pura Appl. 80, 1–122 (1968)
M. Nagumo, Über die Differentialgleichung \(y^{\prime \prime } = f (x, y, y^{\prime })\). Proc. Phys. Math. Soc. Jpn. 19, 861–866 (1937)
H. Poincaré, Les fonctions fuchsiennes et l’équation \(\Delta u = e^{u}\). J. Math. Pures Appl. 4, 137–230 (1898)
S.H. Rasouli, On the existence of positive solution for class of nonlinear elliptic systems with multiple parameters and singular weights. Commun. Korean Math. Soc. 27, 557–564 (2012)
V. Rădulescu, Qualitative Analysis of Nonlinear Elliptic Partial Differential Equations: Monotonicity, Analytic, and Variational Methods, Contemporary Mathematics and Its Applications, vol. 6 (Hindawi Publishing Corporation, New York, 2008)
P. Tolksdorf, Regularity for a more general class of quasilinear elliptic equations. J. Differ. Equ. 51, 126–150 (1984)
B. Xuan, The eigenvalue problem for a singular quasilinear elliptic equation. Electron. J. Differ. Equ. 16, 1–11 (2004)
Acknowledgments
The authors are grateful to the anonymous referee for the careful reading of the paper and numerous useful suggestions. V. Rădulescu acknowledges the support through Grant CNCS PCE-47/2011.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Afrouzi, G.A., Rădulescu, V.D. & Shakeri, S. Positive solutions of singular elliptic systems with multiple parameters and Caffarelli–Kohn–Nirenberg exponents. Period Math Hung 70, 145–152 (2015). https://doi.org/10.1007/s10998-014-0070-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10998-014-0070-z