Abstract
Efficient radio resource management is a key issue in a multi-channel femtocell system, where femtocell base stations are deployed randomly and will generate interference to each other. In this research, we formulate multi-channel power allocation as a convex optimization problem, in order to maximize the overall system throughput under complex transmit power constraint. We apply the Lagrangian duality techniques to make the problem decomposable and propose a distributed iterative subgradient algorithm, namely Multi-channel Power Allocation and Optimization (McPAO). Specifically, McPAO consists of two phases: (I) a gradient projection algorithm to solve the optimal power allocation for each channel under a fixed Lagrangian dual cost; and (II) a subgradient algorithm to update the Lagrangian dual cost by using the power allocation results from Phase I. This two-phase iteration process continues until the Lagrangian dual cost converges to the optimal value. Numerical results show that our McPAO algorithm can improve the overall system throughput by 18 %, comparing to with fixed power allocation schemes. In addition, we study the impact of errors in gradient direction estimation (Phase I), which are caused by limited or delayed information exchange among femtocells in realistic situations. These errors will be propagated into the subgradient algorithm (Phase II) and, subsequently, affect the overall performance of McPAO. A rigorous analytical approach is developed to prove that McPAO can always achieve a bounded overall throughput performance very close to the global optimum.









Similar content being viewed by others
Notes
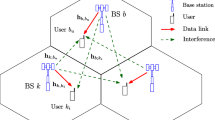
Note that the subset of a femtocell’s neighboring femtocells is time-varying as the environment and channel conditions vary with the time. We denote the subset of neighboring femtocells for femtocell m at time k by \(S_m^k\). For example, in Fig. 1, \(S_1^k\) and \(S_9^k\) are the two subsets for femtocell 1 and femtocell 9 at time k, respectively.
In order to inform the connectivity of the femtocell network, we define \((\mathbb{M},E_{k+1})\) to be the graph of the femtocell network with edges \(E_{k+1}=\{(j,m):j\in S_m^{k + 1},m\in \mathbb{M}\}\). We assume that there exists a scalar Q such that the graph \((\mathbb{M},\bigcup_{q=1,...,Q}E_{k+q})\) is strongly connected for all k.
The variable \(\lambda _{m}^{(l)}\) is the Lagrangian multiplier for femtocell m at the l-th subgradient iteration of Phase II.
References
3GPP TS 36.423 (2010) X2 application protocol
Bertsekas DP (1995) Non-linear programming. Athena Scientific
Bertsekas DP (2005) Non-linear programming (solutions manual), 2nd edn. Available on: http://www.athenasc.com/nlpsol6.pdf
Boyd S, Vandenberghe L (2004) Convex optimization. Cambridge University Press, Cambridge
Chandrasekhar V, Andrews JG, Shen ZK, Muharemovic T, Gatherer A (2009) Distributed power control in femtocell-underlay cellular networks. In: IEEE global telecommunications conference, pp 1–6
Chiang M, Tan CW, Palomar DP, O’Neill D, Julian D (2007) Power control by geometric programming. IEEE Trans Wirel Commun 2007(6):2640–2651
Chiang M, Hande P, Lan T, Tan CW (2008) Power control in wireless cellular networks. Found Trends Network 2008(2):381–533
Huang JW, Vijay GS, Rajeev A, Randall B (2009) Downlink scheduling and resource allocation for OFDM systems. IEEE Trans Wirel Commun 2009(8):288–296
Huang JW, Vijay GS, Rajeev A, Randall B (2010) Joint scheduling and resource allocation in uplink OFDM systems for broadband wireless access networks. IEEE J Sel Areas Commun 2010(27):226–234
Kang X, Liang YC, Garg HK (2011) Distributed power control for spectrum-sharing femtocell networks using stackelberg game. In: IEEE international conference on communications, pp 1–5
Leaves PM, Tafazolli K (2004) Dynamic spectrum allocation in composite reconfigurable wireless networks. IEEE Commun Mag 2004(42):72–81
Lee C, Huang J, Wang L (2010) Distributed channel selection principles for femtocells with two-tier interference. In: IEEE vehicular technology conference, pp 1–5
Mehdi B, Jonas K, Peter L, Andreas S (2009) Intermediate report on system aspects of flexible spectrum use. In: Wireless world initiative new radio-WINNER+D1.6
Ram SS, Nedic A, Veeravalli VV (2008) Distributed stochastic subgradient projection algorithm for convex optimization. J Optim Theory Appl 2008(147):516–545
Ram SS, Veeravalli VV, Nedic A (2009) Distributed non-autonomous power control thorugh distributed convex optimization. In: IEEE computer and communications conference (Infocom), vol 2009, pp 3001–3005
Vijay GS, Randall AB, Rajeev A (2010) Joint scheduling and resource allocation in CDMA systems. IEEE Trans Inf Theory 2010(56):2416–2432
Wang Y, Zheng K, Shen X, Wang W (2011) A distributed resource allocation scheme in femtocell networks. In: IEEE 73rd vehicular technology conference, pp 1–5
Yu W, Lui R (2006) Dual methods for nonconvex spectrum optimization of multicarrier systems. IEEE Trans Commun 2006(54):1310–1322
Zhang JM, Zhang ZY, Wu K, Huang AP (2010) Optimal distributed subchannel, rate and power allocation algorithm in OFDM-based two-tier femtocell networks. In: IEEE vehicular technology conference, pp 1–5
Acknowledgements
This work is sponsored by International Cooperation Program of China under Grant 2012DFG11910, NSFC under grant 61100238, National Science and Technology Major Project under grant 2012ZX03003-009, Key Project of Shanghai Municipality under grant 09511501100, and Shanghai Rising-Star Program (A-type) under Grant 10QA1406300.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof A
As it is proposed in Section 4 that for a given \(\boldsymbol{\lambda}\),
where \(F_n \left( {{ \textbf{x}}_n }|\boldsymbol{\lambda}\right) = \sum\limits_{m = 1}^M {f_{m,n} \left( {{ \textbf{x}}_n }|\boldsymbol{\lambda} \right)} = - \sum\limits_{m = 1}^M \left( R_{m,n} \left( {{\textbf{x}}_n } \right)\right. \left.- \lambda _m e^{x_{m,n} } \right)\).
where \(G(\textbf{x}_n ) = \nabla t\left( \boldsymbol{\lambda} \right)\). And then
and
So
Then substitute Eq. 43 into Eqs. 42,
This equation yields to our conclusion in Eq. 36. □
Proof B
\(\nabla t = - D\) is an ζ -subgradient at \(\boldsymbol\lambda ^{\left( l \right)} \). A solution for Exercise 6.3.13 in [2] is presented in [3]. According to the solution,we have
Together with Eqs. 34 and 35, we have \(d(\boldsymbol{\lambda} ) = - t(\boldsymbol{\lambda} )\). Then we have
Thus we accomplish the proof of Theorem 1. The optimal solution to \(\max \left( {\sum\limits_n^{} {T_n } } \right)\) could be achieved using our scheme. □
Rights and permissions
About this article
Cite this article
Zheng, X., Xu, J., Wang, J. et al. McPAO: A Distributed Multi-channel Power Allocation and Optimization Algorithm for Femtocells. Mobile Netw Appl 17, 648–661 (2012). https://doi.org/10.1007/s11036-012-0407-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11036-012-0407-x