Robust Filter-and-forward Beamforming Design for Two-way Multi-antenna Relaying Networks

Abstract

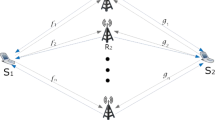
In this paper, we investigate a robust filter-and-forward (FF) beamforming design for two-waymulti-antenna relaying networks, where multiple relays assist two terminals to exchange information. With Gaussian distributed channel errors, the proposed robust beamforming design aims at maximizing the signal-to-interference-plus-noise-ratio (SINR) under individual transmit power constraints at each relay. Exploiting the elegant convex optimization mathematical tools, the optimization problem can be efficiently solved. Finally, simulation results demonstrate that the proposed robust beamformer reduces the sensitivity of the two-way multi-antenna relay networks to channel estimation errors, and outperforms the algorithm with estimated channels only. Moreover, the length of robust beamformer also influences the system performance.

Appendix A

Based on the following expressions, i.e. $\mathbb {E}\{{\mathbf {X}}{\mathbf {X}}^{\textnormal {H}}\}$, $\mathbb {E}\{{\mathbf {Y}}{\mathbf {A}}{\mathbf {Y}}^{\textnormal {H}}\}$ and $\mathbb {E}\{{\mathbf {Y}}{\mathbf {X}}{\mathbf {X}}^{\textnormal {H}}{\mathbf {Y}}^{\textnormal {H}}\}$, the terms with respect to the estimation errors in Eqs. 12, 19, 21 and 24 can be calculated, in which ${\mathbf {X}}$, ${\mathbf {Y}}$, ${\mathbf {A}}$ can be written as

$$\begin{array}{rll}{\mathbf{X}}(p,:)&=&[{\mathbf{0}}_{1\times(k+i)},~x_{j,0},\ldots,x_{j,L_{1}-1},{\mathbf{0}}_{1\times(L_{b}+L_{1}-2-k-i)}], \\{\mathbf{Y}}(q,:)&=&[{\mathbf{0}}_{1\times((m-1)\Omega L_{b} L_{1} k\Omega L_{b}+i\Omega+l-1)},~x_{j,0},~{\mathbf{0}}_{1\times(\Omega L_{b}-1)}, \\&&x_{j,1},{\mathbf{0}}_{1\times((N_{R}-m-1)\Omega L_{b} L_{1}-(k+L_{1}-1)\Omega L_{b}-i\Omega-L_{1}-l-1)},\ldots, \\&&x_{j,L_{1}-1},{\mathbf{0}}_{1\times((L_{b}-i)\Omega-j)}], \\{\mathbf{A}}(p,p')&=&\{a_{p,p'}\}, \\p&=&(m-1)\Omega L_{b} L_{1} +k\Omega L_{b}+i\Omega+j, \\q&=&(m-1)\Omega^{2} L_{b}+i\Omega^{2}+(l-1)\Omega+j, \\p'&=&(m'-1)\Omega L_{b} L_{1}+k'\Omega L_{b}+i'\Omega+j', \\k,k'&=&0,\ldots,L_{1}-1, \\&&i,i'=0,\ldots,L_{b}-1, \\&&j,j'=1,\ldots,\Omega, \\l,l'&=&1,\ldots,\Omega, \\&&m,m'=1,\ldots,\Psi,\end{array}$$

(28)

where ${\mathbf {X}}(p,:)$ denotes the pth row of the matrix ${\mathbf {X}}$ and ${\mathbf {A}}(p,p')$ denotes the pth row and the p’th column element of the matrix ${\mathbf {A}}$. In this Appendix, we assume that $L_{1}=L_{h}(L_{g})$, $\Omega =M_{R}$ and $\Psi =N_{R}$.

1.1 A.1 $\mathbb {E}\{{\textbf {X}}{\textbf {X}}^{\textnormal {H}}\}$

It is easy to find that

$$ \mathbb{E}\{{\mathbf{X}}{\mathbf{X}}^{\textnormal{H}}\}(p,p') =\mathbb{E}\{{\mathbf{X}}(p,:){\mathbf{X}}^{\textnormal{H}}(p',:)\}, $$

(29)

Due to the statistic independence of the channel estimation error and the definitions in Eq. 2 the above equation can be derived as

$$ \mathbb{E}\{{\mathbf{X}}{\mathbf{X}}^{\textnormal{H}}\}(p,p') = L_{1},~when~{\mathbf{X}}(p,:)={\mathbf{X}}(p',:).$$

(30)

1.2 A.2 $\mathbb {E}\{{\mathbf {Y}}{\mathbf {A}}{\mathbf {Y}}^{\textnormal {H}}\}$

The matrix ${\mathbf {Y}}{\mathbf {A}}$equals to

$$\begin{array}{rll} \{{\mathbf{Y}}{\mathbf{A}}\}(\alpha,d) &=& \sum\limits_{k=0}^{L_{1}-1}{x_{j,k}a_{(m-1)\Omega L_{b} L_{1}+k\Omega L_{b}+i\Omega+j,d}}, \\\alpha&=&(m-1)\Omega^{2} L_{b}+i\Omega^{2}+(l-1)\Omega+j, \\d&=& 1,\ldots,\Omega L_{b}L_{1}N_{R}.\end{array}$$

(31)

Then, the product ${\mathbf {Y}}{\mathbf {A}}{\mathbf {Y}}^{\textnormal {H}}$ is formulated as follows

$$\begin{array}{rll} \{{\mathbf{Y}}{\mathbf{A}}{\mathbf{Y}}^{\textnormal{H}}\}(\alpha,\beta)&=&\sum\limits_{k=0}^{L_{1}-1}\sum \limits_{k'=0}^{L_{1}-1}{x_{j,k}~a_{(m-1)\Omega L_{b} L_{1}+k\Omega L_{b}+i\Omega+j,d}~x_{j',k'}} \\&=&\sum\limits_{k=0}^{L_{1}-1}\sum \limits_{k'=0}^{L_{1}-1}{a_{(m-1)\Omega L_{b} L_{1}+k\Omega L_{b}+i\Omega+j,d}~x_{j,k}~x_{j',k'}}, \\ \alpha&=&(m-1)\Omega^{2} L_{b}+i\Omega^{2}+(l-1)\Omega+j, \\ \beta&=&(m'-1)\Omega^{2} L_{b}+i'\Omega^{2}+(l'-1)\Omega+j', \\ i,i'&=&0,\ldots,L_{b}-1, \\ j,j'&=&1,\ldots,\Omega.\end{array}$$

(32)

If $j=j'$ and $k=k'$, then $\mathbb {E}\{x_{j,k}~x_{j',k'}\}=1$, otherwise $\mathbb {E}\{x_{j,k}~x_{j',k'}\}=0$. Therefore, Eq. 32 can be rewritten as

$$\begin{array}{rll} \mathbb{E}\{{\mathbf{Y}}{\mathbf{A}}{\mathbf{Y}}^{\textnormal{H}}\}(\alpha,\beta)&=&~\mathbb{E}\{{\mathbf{Y}}(\alpha,:){\mathbf{A}}{\mathbf{Y}}^{\textnormal{H}}(:,\beta)\}\nonumber\\&=&\displaystyle\sum\limits_{k=0}^{L_{1}-1}\displaystyle\sum\limits_{k'=0}^{L_{1}-1}a_{(m-1)\Omega L_{b} L_{1} + k\Omega L_{b} + \alpha,~(m'-1)\Omega L_{b} L_{1} + k'\Omega L_{b} + \beta} \\\alpha&=&1,\ldots,\Omega L_{b},~~~~~ \beta=1,\ldots,\Omega L_{b}.\end{array}$$

(33)

1.3 A.3 $\mathbb {E}\{{\mathbf {Y}}{\mathbf {X}}{\mathbf {X}}^{\textnormal {H}}{\mathbf {Y}}^{\textnormal {H}}\}$

According to the statistic independence of matrix, we can calculate $\mathbb {E}\{{\mathbf {Y}}{\mathbf {X}}{\mathbf {X}}^{\textnormal {H}}{\mathbf {Y}}^{\textnormal {H}}\}$ by using the results of Eqs. 30 and 33.