Abstract
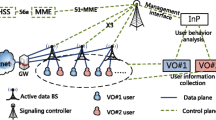
Economic and technical features are equally important to radio resource allocation in wireless network virtualization (WNV). Regarding virtual resource (VR) as commodity, this paper proposes an effective VR allocation scheme for WNV from the perspective of the market-equilibrium theory. First, physical meaning clear utility functions are defined to characterize the network benefits of user equipments (UEs), infrastructure providers (InPs) and virtual network operators (VNOs) in WNV. Then, the VR allocation problem between one InP and multiple VNOs is formulated as a multi-objective optimization problem. To reduce the algorithm complexity, the multiple-objective problem is first decoupled into two single-objective sub-problems. The supplier-layer sub-problem aims to maximize the benefit of the unique InP, while the customer-layer sub-problem aims to maximize the benefits of the multiple VNOs. Both of the separated sub-problems are solved by using standard convex optimization method, and are combined by searching for the equilibrium-price (EP) of the VR market. As a result, the Pareto optimal solution of the original multi-objective problem is found, at which no one (the InP or anyone of the VNOs) can increase its benefit by deviating the EP without hurting others’ benefits. The effectiveness of the proposed VR allocation scheme is testified through extensive experiments.










Similar content being viewed by others
Notes
The proof for the uniqueness is given in Proposition 5.
References
Duan Q, Yan Y, Vasilakos A (2012) A survey on service-oriented network virtualization toward convergence of networking and cloud computing. IEEE Trans Netw Serv Manag 9(4):373–392
Fischer A, Botero J, Beck M, De Meer H, Hesselbach X (2013) Virtual network embedding: a survey. IEEE Commun Surv Tutorials 15(4):1888–1906
Zhang H, Jiang C, Cheng J, Leung VCM (2015) Cooperative interference mitigation and handover management for heterogeneous cloud small cell networks. IEEE Wirel Commun 22(3):92–99
Chowdhury N, Boutaba R (2009) Network virtualization: state of the art and research challenges. IEEE Commun Mag 47(7):20–26
Wen H, Tiwary PK, Le-Ngoc T (2013) Wireless virtualization. Springer
Wang X, Krishnamurthy P, Tipper D (2013) Wireless network virtualization. In: Proc. International Conference on Computing, Networking and Communications (ICNC), IEEE, San Diego, CA, pp 818–822
Liang C, Yu FR (2014) Wireless network virtualization: a survey, some research issues and challenges. IEEE Commun Surv Tutorials PP(99):1–24
Zhang H, Jiang C, Beaulieu NC, Chu X, Wen X, Tao M (2014) Resource allocation in spectrum -sharing OFDMA femtocells with heterogeneous services. IEEE Trans Commun 62(7):2366–2377
Zhou Y, Li Y, Sun G, Jin D, Su L, Zeng L (2010) Game theory based bandwidth allocation scheme for network virtualization. In: Proc. Global Telecommunications Conference (Globecom), IEEE, Miami, FL, pp 1–5
Liu B, Tian H (2013) A bankruptcy game-based resource allocation approach among virtual mobile operators. IEEE Commun Lett 17(7):1420–1423
Kokku R, Mahindra R, Zhang H, Rangarajan S (2012) NVS: a substrate for virtualizing wireless resources in cellular networks. IEEE/ACM Trans Networking 20(5):1333–1346
Lu X, Yang K, Liu Y, Zhou D, Liu S (2012) An elastic resource allocation algorithm enabling wireless network virtualization. Wiley Wireless Commun. & Mobile Computing, pp 1–14
Lu X, Yang K, Zhang H (2014) An elastic sub-carrier and power allocation algorithm enabling wireless network virtualization. Springer Wirel Pers Commun 75(4):1827–1849
Zhang G, Yang K, Wei J, Xu K, Liu P (2015) Virtual resource allocation for wireless virtualization networks using market equilibrium theory. To appear in IEEE INFOCOM 2015 Workshop on Mobile Cloud and Virtualization, Hong Kong, pp 1–6
Osborne MJ, Rubinstein A (1994) A course in game theory. MIT press
Deb D (2014) Multi-objective optimization. Springer Search Methodologies, pp 403–449
Nicholson W, Snyder C (2011) Microeconomic theory: basic principles and extensions. Cengage Learning
Zhang H, Chu X, Guo W, Wang S (2015) Coexistence of Wi-Fi and heterogeneous small cell networks sharing unlicensed spectrum. IEEE Commun Mag 53(3):158–164
Xu C, Sheng M, Yang C, Wang X, Wang L (2014) Pricing-based multiresource allocation in OFDMA cognitive radio networks: an energy efficiency perspective. IEEE Trans Veh Technol 63(5):2336–2348
Zhang H, Jiang C, Beaulieu NC, Chu X, Wang X, Quek T (2015) Resource allocation for cognitive small cell networks: a cooperative bargaining game theoretic approach. IEEE Trans Wirel Commun 14(6):3481–3493
Zhang J, Zhang Q (2009) Stackelberg game for utility-based cooperative cognitive radio networks. In Proc. ACM 17th Annual International Conference on Mobile Computing and Networking, (MobiHoc’09), pp 23–31
Lin H, Chatterjee M, Das SK et al (2005) ARC: an integrated admission and rate control framework for competitive wireless CDMA data networks using noncooperative games. IEEE Trans Mob Comput 4(3):243–258
Nemhauser GL, Wolsey LA (1988) Integer and combinatorial optimization. Wiley, New York
Song G, Li Y (2005) Cross-layer optimization for OFDM wireless networks-part I: theoretical framework. IEEE Trans Wirel Commun 4(2):614–624
Mas-Colell A, Whinston MD, Green JR (1995) Microeconomic Theory. Oxford University Press
Giupponi L, Ibars C (2009) Distributed cooperation among cognitive radios with complete and incomplete information. EURASIP J Adv Signal Process 2009:1–13
Acknowledgments
This work was supported in part by the Shenzhen S&T Innovation Project under Grant JCYJ20140610151856732, in part by the National Natural Science Foundation of China under Grant 61471361, 61572389, 61572191, and 61371127, in part by the National High-Tech R&D Program (863 Program) under Grant 2015AA01A705, and in part by the Natural Science Foundation of Jiangsu Province, China under Grant BK20140202.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
1.1 Proof of proposition 1
Taking the first- and second- order derivatives of π0(α) with respect to c m , we have
and
In order to guarantee the concavity of π0(α), it is ordered to derive the condition under which ∂π0(α)/∂c m > 0. By substituting Eq. (4) into Eq. (26), the condition is derived as shown in Eqs. (12) and (13).
Appendix B
2.1 Proof of proposition 2
To solve problem (10), we exploit the Karush-Kuhn-Tucker (KKT) optimality condition [21]. The Lagrangian function of problem (10) is written as
where μ, v m and ρ m , ∀ m = 1, …, M, are the non-negative Lagrangian multipliers. The KKT optimality conditions for this problem are:
with the additional complementary slackness conditions as:
Since 0 < c m < S and ∑ M m = 1 c m < S for ∀ m = 1, …, M, constraints (10.1), (10.2) and (10.3) are all satisfied without equality. So we get v m = 0, ρ m = 0 and μ = 0. Then, by solving Eq. (29), we can obtain the optimal solution to problem (10) as shown in Eq. (14).
Appendix C
3.1 Proof of proposition 3
First, we assume that the unique optimal solutionFootnote 1 to problem (16) is
The resultant network benefit for the nth VNO is
We need to prove that Eq. (33) is also a solution (but not necessarily the unique one) to problem (15). This can be proved by following contradiction.
Assume that Eq. (33) is not a solution to problem (15). According to the Pareto optimality, there must exists another VR allocation vector
different from Eq. (33) which can increases the benefits of part of the VNOs without decreasing the benefits for the other VNOs. Without loss of generality, we assume that, with the new VR allocation vector (35), the benefits of the N − 1 VNOs remain unchanged except for the \( \overline{n} \)th VNO. That means
and
On condition that Proposition 4 is satisfied, π n would increase monotonically with c n,k , for ∀ k ∈ {1, …, K n }. Thus, to increase \( {\tilde{\uppi}}_{\overline{n}} \), we have to allocate more VR to the \( \overline{n} \)th VNO. As the total amount of VR available for the N VNOs is fixed, one or some of the N − 1 VNOs (other than the \( \overline{n} \)th VNO) would receive reduced amount of VR. This contradicts with the assumption that the VR allocation vector (35) is Pareto optimality.
Rights and permissions
About this article
Cite this article
Zhang, G., Yang, K., Jiang, H. et al. Equilibrium Price and Dynamic Virtual Resource Allocation for Wireless Network Virtualization. Mobile Netw Appl 22, 564–576 (2017). https://doi.org/10.1007/s11036-016-0766-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11036-016-0766-9