Skip to main content

Advertisement

SpringerLink
Log in

Outage Performance of Energy Harvesting DF Relaying NOMA Networks

  • Published:
Mobile Networks and Applications Aims and scope Submit manuscript

Abstract

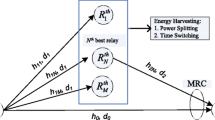
In this paper, we investigate energy harvesting decode-and-forward relaying non-orthogonal multiple access (NOMA) networks. We study two cases of single relay and multiple relays with partial relay selection strategy. Specifically, one source node wishes to transmit two symbols to two respective destinations directly and via the help of one selected intermediate energy constraint relay node, and the NOMA technique is applied in the transmission of both hops (from source to relay and from relay to destinations). For performance evaluation, we derive the closed-form expressions for the outage probability (OP) at D 1 and D 2 with both cases of single and multiple relays. Our analysis is substantiated via Monte Carlo simulation. The effect of several parameters, such as power allocation factors in both transmissions in two hops, power splitting ratio, energy harvesting efficiency, and the location of relay nodes to the outage performances at the two destinations is investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Raghunathan V, Ganeriwal S, Srivastava M (2006) Emerging techniques for long lived wireless sensor networks. IEEE Commun Mag 44(4):108–114

    Article  Google Scholar 

  2. Paradiso JA, Starner T (2005) Energy scavenging for mobile and wireless electronics. IEEE Pervasive Comput 4(1):18–27

    Article  Google Scholar 

  3. Ulukus S, Yener A, Erkip E, Simeone O, Zorzi M, Grover P, Huang K (2015) Energy harvesting wireless communications: a review of recent advances. IEEE J Select Areas Commun 33(3):360–381

    Article  Google Scholar 

  4. Medepally B, Mehta NB (2010) Voluntary energy harvesting relays and selection in cooperative wireless networks. IEEE Trans Wirel Commun 8(11):3543–3553

    Article  Google Scholar 

  5. Zhou X, Zhang R, Ho CK (2013) Wireless information and power transfer: architecture design and rate-energy tradeoff. IEEE Trans commun 61(11):4754–4767

    Article  Google Scholar 

  6. Zhang R, Ho CK (2013) MIMO broadcasting for simultaneous wireless information and power transfer. IEEE Trans Wirel Commun 12(5):1989–2001

    Article  Google Scholar 

  7. Varshney LR (2008) Transporting information and energy simultaneously. IEEE International Symposium on Information Theory (ISIT), Toronto, pp 1612–1616

    Google Scholar 

  8. Liu L, Zhang R, Chua KC (2013) Wireless information transfer with opportunistic energy harvesting. IEEE Trans Wirel Commun 12(1):288–300

    Article  Google Scholar 

  9. Nasir AA, Zhou X, Durrani S, Kennedy RA (2013) Relaying protocols for wireless energy harvesting and information processing. IEEE Trans Wirel Commun 12(7):3622–3636

    Article  Google Scholar 

  10. Nasir AA, Zhou X, Durrani S, Kennedy RA (2015) Wireless-powered relays in cooperative communications: time-switching relaying protocols and throughput analysis. IEEE Trans Commun 63(5):1607–1622

    Article  Google Scholar 

  11. Ding Z, Perlaza SM, Esnaola I, Poor HV (2014) Power allocation strategies in energy harvesting wireless cooperative networks. IEEE Trans Wirel Commun 13(2):846–860

    Article  Google Scholar 

  12. Liu Y, Wang L, Elkashlan M, Duong TQ (2014) Two-way relaying networks with wireless power transfer: policies design and throughput analysis. IEEE Global Communications Conference (GLOBECOM), Austin, pp 4030–4035

    Google Scholar 

  13. Son PN, Kong HY (2015) Energy-harvesting relay selection schemes for decode-and-forward dual-hop networks. IEICE Trans Commun E98-B(4):661–672

    Article  Google Scholar 

  14. Yuen C, Elkashlan M, Qian Y, Duong TQ, Shu L, Schmidt F (2015) Energy harvesting communications: Part 1 [Guest Editorial]. IEEE Commun Mag 53(4):68–69

    Article  Google Scholar 

  15. Yuen C, Elkashlan M, Qian Y, Duong TQ, Shu L, Schmidt F (2015) Energy harvesting communications: Part 2 [Guest Editorial]. IEEE Commun Mag 53(6):54–55

    Article  Google Scholar 

  16. Yuen C, Elkashlan M, Qian Y, Duong TQ, Shu L, Schmidt F (2015) Energy harvesting communications: Part 3 [Guest Editorial]. IEEE Commun Mag 53(8):90–91

    Article  Google Scholar 

  17. Doan TX, Hoang T, Duong TQ, Ngo HQ (2017) Energy harvesting-based D2D networks in the presence of interference and ambient RF sources. IEEE access, PP(99), https://doi.org/10.1109/ACCESS.2017.2681696

    Article  Google Scholar 

  18. Pejoski S, Hadzi-Velkov Z, Duong TQ, Zhong C (2017) Wireless powered communication networks with non-ideal circuit power consumption. IEEE Communications Letters, PP(99), https://doi.org/10.1109/LCOMM.2017.2680446

    Article  Google Scholar 

  19. Tam HHM, Tuan HD, Nasir AA, Duong TQ, Poor HV (2017) MIMO Energy Harvesting in Full-Duplex Multi-user Networks. PP(99), https://doi.org/10.1109/TWC.2017.2679055

    Article  Google Scholar 

  20. Hoang T, Duong TQ, Vo NS, Kundu C (2017) Physical layer security in cooperative energy harvesting networks with a friendly jammer. IEEE Wirel Commun Lett 6(2):174–177

    Article  Google Scholar 

  21. Nasir AA, Tuan HD, Ngo DT, Duong TQ, Poor HV (2017) Beamforming design for wireless information and power transfer systems: receive power-splitting versus transmit time-switching. IEEE Trans Commun 65(2):876–889

    Article  Google Scholar 

  22. Nasir AA, Tuan HD, Duong TQ, Poor HV (2017) Secrecy rate beamforming for multi-cell networks with information and energy harvesting. IEEE Trans Singal Process 65(3):677–689

    Article  Google Scholar 

  23. Jiang X, Zhong C, Chen X, Duong TQ, Tsiftsis TA, Zhang Z (2016) Secrecy performance of wirelessly powered wiretap channels. IEEE Trans Commun 64(9):3858–3871

    Article  Google Scholar 

  24. Nguyen NP, Duong TQ, Ngo HQ, Hadzi-Velkov Z, Shu L (2016) Secure 5G wireless communications: a joint relay selection and wireless power transfer approach. IEEE Access 4:3349–3359

    Article  Google Scholar 

  25. Hadzi-Velkov Z, Nikoloska I, Karagiannidis GK, Duong TQ (2016) Wireless networks with energy harvesting and power transfer: joint power and time allocation. IEEE Signal Process Lett 23(6):50–54

    Article  Google Scholar 

  26. Liu Y, Wang L, Zaidi SAR, Elkashlan M, Duong TQ (2016) Secure D2D communication in large-scale cognitive cellular networks: a wireless power transfer model. IEEE Trans Commun 64(1):329–342

    Article  Google Scholar 

  27. Hadzi-Velkov Z, Zlatanov N, Duong TQ, Schober R (2015) Rate maximization of decode-and-forward relaying systems with RF energy harvesting. IEEE Commun Lett 19(12):2290–2293

    Article  Google Scholar 

  28. Ding Z, Peng M, Poor HV (2015) Cooperative non-orthogonal multiple access in 5G systems. IEEE Commun Lett 19(8):1462–1465

    Article  Google Scholar 

  29. Do NT, Costa DBD, Duong TQ, An B (2017) A BNBF user selection scheme for noma-based cooperative relaying systems with SWIPT. IEEE Commun Lett 21(3):664–667

    Article  Google Scholar 

  30. Lee S, Costa DBd, Vien QT, Duong TQ, De Sousa Jr. RT (2016) Non-orthogonal multiple access schemes with partial relay selection. IET Communications, https://doi.org/10.1049/iet-com.2016.0836

    Article  Google Scholar 

  31. Liu Y, Ding Z, Elkashlan M, Yuan J (2016) Non-orthogonal multiple access in large-scale underlay cognitive radio networks. IEEE Trans Veh Technol 65(12):10152–1015

    Article  Google Scholar 

  32. Men J, Ge J (2015) Performance analysis of non-orthogonal multiple access in downlink cooperative network. IET Commun 9(18):2267–2273

    Article  Google Scholar 

  33. Kim J-B, Lee I-H (2015) Non-orthogonal multiple access in coordinated direct and relay transmission. IEEE Commun Lett 19(11):2037–2040

    Article  Google Scholar 

  34. Diamantoulakis PD, Pappi KN, Ding Z, Karagiannidis GK (2016) Optimal design of non-orthogonal multiple access with wireless power transfer. IEEE International Conference on Communications (ICC), Kuala Lumpur, pp 1–6

    Google Scholar 

  35. Liu Y, Ding Z, Elkashlan M, Poor HV (2016) Coperative non-orthogonal multiple access with simultaneous wireless information and power transfer. IEEE J Sel Areas Commun 33 (4):938– 953

    Article  Google Scholar 

  36. Gradshteyn IS, Ryzhik IM (2007) Table of integrals, series and products, 7th edn. Academic Press, Cambridge

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Duy Tan University, Da Nang, Vietnam

    Dac-Binh Ha & Sang Quang Nguyen

Authors
  1. Dac-Binh Ha
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sang Quang Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sang Quang Nguyen.

Appendices

Appendix A: Finding the closed-form of probabilty \(\Pr \left [{g_{1}} \geqslant {u_{1}},{g_{2}} < \frac {u_{2}}{g_{1}} \right ]\)

By using the PDF of RV g 1 and CDF of RV g 2, the probabilty \(\Pr \left [ {g_{1}} \geqslant {u_{1}},{g_{2}} < \frac {u_{2}}{g_{1}} \right ]\) can be obtained as

$$ \begin{array}{ll} \Pr \left[ {{g_{1}} \geqslant {u_{1}},{g_{2}} < \frac{{{u_{2}}}}{{{g_{1}}}}} \right] = \int\limits_{{u_{1}}}^{\infty} {{f_{{g_{1}}}}\left( x \right)} {F_{{g_{2}}}}\left( {\frac{{{u_{2}}}}{x}} \right)dx \hfill \\ = \int\limits_{{u_{1}}}^{\infty} {{\lambda_{1}}{e^{ - {\lambda_{1}}x}}\left( {1 - {e^{ - \frac{{{\lambda_{2}}{u_{2}}}}{x}}}} \right)dx} \hfill \\ = e^ - {\lambda_{1}}{u_{1}} - \underbrace {\int\limits_{{u_{1}}}^{\infty} {{\lambda_{1}}{e^{ - {\lambda_{1}}x}}{e^{ - \frac{{{\lambda_{2}}{u_{2}}}}{x}}}dx}} _{{I_{1}}} \end{array} $$
(39)

To calculate the integral I 1, we first apply the equation 1.211 of [36]: \({e^{x}} = \sum \limits _{k = 0}^{\infty } {\frac {{{x^{k}}}}{{k!}}} \) to the term \({{e^{ - \frac {{{\lambda _{2}}{u_{2}}}}{x}}}}\) to obtain (A.2.1), then using Eq. 3.381.3 of [36]: \(\int _{u}^{\infty } {{x^{v - 1}}{e^{ - \mu x}}dx} = \frac {1}{{{\mu ^{v}}}}\Gamma \left ({v,\mu u} \right )\) to obtain (A.2.2) as follows

$$ \begin{array}{ll} {I_{1}}\mathop = \limits^{{\text{(A.2.1)}}} {\lambda_{1}}\sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}} {\left( { - {\lambda_{2}}{u_{2}}} \right)^{k}}\int\limits_{{u_{1}}}^{\infty} {\frac{{{e^{ - {\lambda_{1}}x}}}}{{{{\left( x \right)}^{k}}}}dx} \hfill \\ \mathop = \limits^{{\text{(A.2.2)}}} \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}} {\left( { - {\lambda_{1}}{\lambda_{2}}{u_{2}}} \right)^{k}}\Gamma \left( {1 - k,{\lambda_{1}}{u_{1}}} \right) \hfill \end{array} $$
(40)

By substituting (40) into (39), we obtain:

$$ \Pr \left[ {{g_{1}} \geqslant {u_{1}},{g_{2}} < \frac{{{u_{2}}}}{{{g_{1}}}}} \right] = {e^{ - {\lambda_{1}}{u_{1}}}} - \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}} {\left( { - {\lambda_{1}}{\lambda_{2}}{u_{2}}} \right)^{k}}\Gamma \left( {1 - k,{\lambda_{1}}{u_{1}}} \right) $$
(41)

Appendix B: Finding the closed-form of probabilty \(\Pr \left [ {{g_{1b}} \geqslant {u_{1}},{g_{2b}} < \frac {{{u_{2}}}}{{{g_{1b}}}}} \right ]\)

By using the PDF of RV g 1b and CDF of RV g 2b as \({f_{{g_{1b}}}}\left (x \right ) = N{\lambda _{1}}\sum \limits _{n = 0}^{N - 1} {C_{N - 1}^{n}{{\left ({ - 1} \right )}^{n}}{e^{ - \left ({n + 1} \right ){\lambda _{1}}x}}} \) and \({F_{{g_{2b}}}}\left (x \right ) = 1 - {e^{ - {\lambda _{2}}x}}\), we obtain:

$$ \begin{array}{ll} \Pr \left[ {{g_{1b}} \geqslant {u_{1}},{g_{2b}} < \frac{{{u_{2}}}}{{{g_{1b}}}}} \right] = N{\lambda_{1}}\sum\limits_{n = 0}^{N - 1} {C_{N - 1}^{n}{{\left( { - 1} \right)}^{n}}\int\limits_{{u_{1}}}^{\infty} {{e^{ - \left( {n + 1} \right){\lambda_{1}}x}}\left( {1 - {e^{ - \frac{{{\lambda_{2}}{u_{2}}}}{x}}}} \right)dx}} \hfill \\ \mathop = \limits^{{\text{(B.1.1)}}} N{\lambda_{1}}\sum\limits_{n = 0}^{N - 1} {C_{N - 1}^{n}{{\left( { - 1} \right)}^{n}}\left( {\int\limits_{{u_{1}}}^{\infty} {{e^{ - \left( {n + 1} \right){\lambda_{1}}x}}dx} - \int\limits_{{u_{1}}}^{\infty} {{e^{ - \left( {n + 1} \right){\lambda_{1}}x}}{e^{ - \frac{{{\lambda_{2}}{u_{2}}}}{x}}}dx}} \right)} \hfill \\ \mathop = \limits^{{\text{(B.1.2)}}} {N\sum\limits_{n = 0}^{N - 1} {C_{N - 1}^{n}{{\left( { - 1} \right)}^{n}}\left( {\frac{{{e^{ - \left( {n + 1} \right){\lambda_{1}}{u_{1}}}}}}{{\left( {n + 1} \right)}} - \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}} {{\left( { - {\lambda_{1}}{\lambda_{2}}{u_{2}}} \right)}^{k}}{ {\left( {n + 1} \right)}^{k - 1}}\Gamma \left( {1 - k,\left( {n + 1} \right){\lambda_{1}}{u_{1}}} \right)} \right)}} \hfill \end{array} $$
(42)

where (B.1.2) is obtained from (B.1.1) by first using Eq. 1.211 of [36] to the term \({{e^{ - \frac {{{\lambda _{2}}{u_{2}}}}{x}}}}\), then applying Eq. 3.381 of [36].

Appendix C: Proof of Eqs. 34 and 37

First, for the case of a 1 < a 2(1 + γ t ), the probability OP 6.2 in Eq. 31 can be rewritten as

$$ \begin{array}{l} O{P_{6.2}}|_{{a_{1}} < {a_{2}}\left( {1 + {\gamma_{t}}} \right)} = \Pr \left[ \begin{array}{l} {g_{1}} \ge \frac{{(1 - \rho + \mu ){\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right)(1 - \rho ){\gamma_{0}}}}\\ \min \left( {\frac{{{b_{1}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}}}}{{{b_{2}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}} + 1 + \mu} },\frac{{{b_{2}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}}}}{{1 + \mu} }} \right) < {\gamma_{t}} \end{array} \right]\\ = \Pr \left[ \begin{array}{l} {g_{1}} \ge \frac{{(1 - \rho + \mu ){\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right)(1 - \rho ){\gamma_{0}}}}\\ \frac{{{b_{1}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}}}}{{{b_{2}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}} + 1 + \mu} } < \frac{{{b_{2}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}}}}{{1 + \mu} },\frac{{{b_{1}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}}}}{{{b_{2}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}} + 1 + \mu} } < {\gamma_{t}} \end{array} \right]\\ + \Pr \left[ \begin{array}{l} {g_{1}} \ge \frac{{(1 - \rho + \mu ){\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right)(1 - \rho ){\gamma_{0}}}}\\ \frac{{{b_{1}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}}}}{{{b_{2}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}} + 1 + \mu} } \ge \frac{{{b_{2}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}}}}{{1 + \mu} },\frac{{{b_{2}}\eta \rho {\gamma_{0}}{g_{1}}{g_{3}}}}{{1 + \mu} } < {\gamma_{t}} \end{array} \right]\\ = \underbrace {\Pr \left[ \begin{array}{l} {g_{1}} \ge \frac{{(1 - \rho + \mu ){\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right)(1 - \rho ){\gamma_{0}}}}\\ {g_{3}} > \frac{{\left( {{b_{1}} - {b_{2}}} \right)\left( {1 + \mu} \right)}}{{{{\left( {{b_{2}}} \right)}^{2}}\eta \rho {\gamma_{0}}{g_{1}}}},{g_{3}} < \frac{{\left( {1 + \mu} \right){\gamma_{t}}}}{{\left( {{b_{1}} - {b_{2}}{\gamma_{t}}} \right)\eta \rho {\gamma_{0}}{g_{1}}}} \end{array} \right]}_{O{P_{6.2.1}}} + \underbrace {\Pr \left[ \begin{array}{l} {g_{1}} \ge \frac{{(1 - \rho + \mu ){\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right)(1 - \rho ){\gamma_{0}}}}\\ {g_{3}} \le \frac{{\left( {{b_{1}} - {b_{2}}} \right)\left( {1 + \mu} \right)}}{{{{\left( {{b_{2}}} \right)}^{2}}\eta \rho {\gamma_{0}}{g_{1}}}},{g_{3}} < \frac{{\left( {1 + \mu} \right){\gamma_{t}}}}{{{b_{2}}\eta \rho {\gamma_{0}}{g_{1}}}} \end{array} \right]}_{O{P_{6.2.2}}} \end{array} $$
(43)

where OP 6.2.1 and OP 6.2.2 are given as

$$ O{P_{6.2.1}} = \left\{ \begin{array}{l} \int\limits_{\frac{{{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}}^{\infty} {{f_{{g_{1}}}}\left( x \right)\left[ {{F_{{g_{3}}}}\left( {\frac{{{\omega_{3}}{\gamma_{t}}}}{{\left( {{b_{1}} - {b_{2}}{\gamma_{t}}} \right){\gamma_{0}}x}}} \right) - {F_{{g_{3}}}}\left( {\frac{{\left( {{b_{1}} - {b_{2}}} \right){\omega_{3}}}}{{{{\left( {{b_{2}}} \right)}^{2}}{\gamma_{0}}x}}} \right)} \right]dx,\,\,\,\,\,\,if\,\,{b_{1}} < {b_{2}}\left( {1 + {\gamma_{t}}} \right)} \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,\,{b_{1}} \ge {b_{2}}\left( {1 + {\gamma_{t}}} \right) \end{array} \right. $$
(44)
$$ \begin{array}{l} O{P_{6.2.2}} = \left\{ \begin{array}{l} \Pr \left[ \begin{array}{l} {g_{1}} \ge \frac{{{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}\\ {g_{3}} \le \frac{{\left( {{b_{1}} - {b_{2}}} \right){\omega_{3}}}}{{{{\left( {{b_{2}}} \right)}^{2}}{\gamma_{0}}{g_{1}}}} \end{array} \right]\,\,\,\,if\,{b_{1}} < {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,\\ \Pr \left[ \begin{array}{l} {g_{1}} \ge \frac{{{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}\\ {g_{3}} < \frac{{{\omega_{3}}{\gamma_{t}}}}{{{b_{2}}{\gamma_{0}}{g_{1}}}} \end{array} \right]\,\,\,\,if\,{b_{1}} \ge {b_{2}}\left( {1 + {\gamma_{t}}} \right)\, \end{array} \right.\\ = \left\{ \begin{array}{l} \int\limits_{\frac{{{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}}^{\infty} {{f_{{g_{1}}}}\left( x \right)\left[ {{F_{{g_{3}}}}\left( {\frac{{\left( {{b_{1}} - {b_{2}}} \right){\omega_{3}}}}{{{{\left( {{b_{2}}} \right)}^{2}}{\gamma_{0}}{g_{1}}}}} \right)} \right]dx,} \,\,\,\,if\,{b_{1}} < {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,\\ \int\limits_{\frac{{{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}}^{\infty} {{f_{{g_{1}}}}\left( x \right)\left[ {{F_{{g_{3}}}}\left( {\frac{{{\omega_{3}}{\gamma_{t}}}}{{{b_{2}}{\gamma_{0}}{g_{1}}}}} \right)} \right]dx,} \,\,\,\,if\,{b_{1}} \ge {b_{2}}\left( {1 + {\gamma_{t}}} \right)\, \end{array} \right. \end{array} $$
(45)

By substituting (44) and (45) into (43), and using the result in Appendix A, we obtain

$$ \begin{array}{l} {\left. {O{P_{6.2}}} \right|_{{a_{1}} < {a_{2}}\left( {1 + {\gamma_{t}}} \right)}} = O{P_{6.2.1}} + O{P_{6.2.2}}\\ = \left\{ \begin{array}{l} \int\limits_{\frac{{{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}}^{\infty} {{f_{{g_{1}}}}\left( x \right)\left[ {{F_{{g_{3}}}}\left( {\frac{{{\omega_{3}}{\gamma_{t}}}}{{\left( {{b_{1}} - {b_{2}}{\gamma_{t}}} \right){\gamma_{0}}{g_{1}}}}} \right)} \right]dx,} \,\,\,\,if\,{b_{1}} < {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,\\ \int\limits_{\frac{{{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}}^{\infty} {{f_{{g_{1}}}}\left( x \right)\left[ {{F_{{g_{3}}}}\left( {\frac{{{\omega_{3}}{\gamma_{t}}}}{{{b_{2}}{\gamma_{0}}{g_{1}}}}} \right)} \right]dx,} \,\,\,\,if\,{b_{1}} \ge {b_{2}}\left( {1 + {\gamma_{t}}} \right)\, \end{array} \right.\\ = {e^{ - \frac{{{\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}}} - \left\{ \begin{array}{l} \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda_{1}}{\lambda_{3}}{\omega_{3}}{\gamma_{t}}}}{{\left( {{b_{1}} - {b_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}} \right)}^{k}}\Gamma \left( {1 - k,\frac{{{\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}} \right),} \,\,\,\,if\,{b_{1}} < {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,\\ \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda_{1}}{\lambda_{3}}{\omega_{3}}{\gamma_{t}}}}{{{b_{2}}{\gamma_{0}}}}} \right)}^{k}}\Gamma \left( {1 - k,\frac{{{\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}} \right)} ,\,\,\,\,if\,{b_{1}} \ge {b_{2}}\left( {1 + {\gamma_{t}}} \right)\, \end{array} \right. \end{array} $$
(46)

Next, we can obtain the result for OP 6.2 in the case of a 1 ≥ a 2(1 + γ t ) from Eq. 47 with replacing ′(a 1 − a 2 γ t )′ by \(^{\prime }a_{2}^{\prime }\) as

$$ {\left. {O{P_{6.2}}} \right|_{{a_{1}} \ge {a_{2}}\left( {1 + {\gamma_{t}}} \right)}} = {e^{ - \frac{{{\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{{a_{2}}{\gamma_{0}}}}}} - \left\{ \begin{array}{l} \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda_{1}}{\lambda_{3}}{\omega_{3}}{\gamma_{t}}}}{{\left( {{b_{1}} - {b_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}} \right)}^{k}}\Gamma \left( {1 - k,\frac{{{\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{{a_{2}}{\gamma_{0}}}}} \right),} \,\,\,\,if\,{b_{1}} < {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,\\ \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}{{\left( { - \frac{{{\lambda_{1}}{\lambda_{3}}{\omega_{3}}{\gamma_{t}}}}{{{b_{2}}{\gamma_{0}}}}} \right)}^{k}}\Gamma \left( {1 - k,\frac{{{\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{{a_{2}}{\gamma_{0}}}}} \right)} ,\,\,\,\,if\,{b_{1}} \ge {b_{2}}\left( {1 + {\gamma_{t}}} \right)\, \end{array} \right. $$
(47)

By combining (46) and (47), we finish the proof for Eq. 34.

In the case of N relays, only the PDF of RV g 1 b is changed. Thus, we can obtain OP 6.2 in case of N relays and a 1 < a 2(1 + γ t ) from Eq. 46 as

$$ \begin{array}{ll} {\left. {OP_{6.2}^{\,N\,relays}} \right|_{{a_{1}} < {a_{2}}\left( {1 + {\gamma_{t}}} \right)}} = \left\{ {\begin{array}{*{20}{l}} {\int\limits_{\frac{{{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}}^{\infty} {{f_{{g_{1b}}}}\left( x \right)\left[ {{F_{{g_{3b}}}}\left( {\frac{{{\omega_{3}}{\gamma_{t}}}}{{\left( {{b_{1}} - {b_{2}}{\gamma_{t}}} \right){\gamma_{0}}{g_{1b}}}}} \right)} \right]dx,} \,\,\,\,if\,{b_{1}} < {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,} \\ {\int\limits_{\frac{{{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}}^{\infty} {{f_{{g_{1}}}}\left( x \right)\left[ {{F_{{g_{3b}}}}\left( {\frac{{{\omega_{3}}{\gamma_{t}}}}{{{b_{2}}{\gamma_{0}}{g_{1b}}}}} \right)} \right]dx,} \,\,\,\,if\,{b_{1}} \geqslant {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,} \end{array}} \right. \\ = \left\{ {\begin{array}{ll} {N\sum\limits_{n = 0}^{N - 1} {C_{N - 1}^{n}{{\left( { - 1} \right)}^{n}}\left( \begin{array}{ll} \frac{{{e^{ - \frac{{\left( {n + 1} \right){\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}}}}}{{\left( {n + 1} \right)}} - \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}} {\left( { - \frac{{{\lambda_{1}}{\lambda_{3}}{\omega_{3}}{\gamma_{t}}}}{{\left( {{b_{1}} - {b_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}} \right)^{k}} \hfill \\ {\left( {n + 1} \right)^{k - 1}}\Gamma \left( {1 - k,\frac{{\left( {n + 1} \right){\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}} \right) \hfill \end{array} \right)} ,\,\,\,\,if\,{b_{1}} < {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,} \\ {N\sum\limits_{n = 0}^{N - 1} {C_{N - 1}^{n}{{\left( { - 1} \right)}^{n}}\left( \begin{array}{ll} \frac{{{e^{ - \frac{{\left( {n + 1} \right){\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}}}}}{{\left( {n + 1} \right)}} - \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}} {\left( { - \frac{{{\lambda_{1}}{\lambda_{3}}{\omega_{3}}{\gamma_{t}}}}{{{b_{2}}{\gamma_{0}}}}} \right)^{k}} \hfill \\ {\left( {n + 1} \right)^{k - 1}}\Gamma \left( {1 - k,\frac{{\left( {n + 1} \right){\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{\left( {{a_{1}} - {a_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}} \right) \hfill \end{array} \right)} ,\,\,\,\,if\,{b_{1}} \geqslant {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,} \end{array}} \right. \end{array} $$
(48)

Similarly, the term OP 6.2 in the case of N relays with a 1 ≥ a 2(1 + γ t ) is expressed as

$$ \begin{array}{ll} {\left. {OP_{6.2}^{\,N\,relays}} \right|_{{a_{1}} \geqslant {a_{2}}\left( {1 + {\gamma_{t}}} \right)}} \hfill \\ = \left\{ {\begin{array}{*{20}{l}} {N\sum\limits_{n = 0}^{N - 1} {C_{N - 1}^{n}{{\left( { - 1} \right)}^{n}}\left( \begin{array}{ll} \frac{{{e^{ - \frac{{\left( {n + 1} \right){\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{{a_{2}}{\gamma_{0}}}}}}}}{{\left( {n + 1} \right)}} - \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}} {\left( { - \frac{{{\lambda_{1}}{\lambda_{3}}{\omega_{3}}{\gamma_{t}}}}{{\left( {{b_{1}} - {b_{2}}{\gamma_{t}}} \right){\gamma_{0}}}}} \right)^{k}} \hfill \\ {\left( {n + 1} \right)^{k - 1}}\Gamma \left( {1 - k,\frac{{\left( {n + 1} \right){\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{{a_{2}}{\gamma_{0}}}}} \right) \hfill \end{array} \right)} ,\,\,\,\,if\,{b_{1}} < {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,} \\ {N\sum\limits_{n = 0}^{N - 1} {C_{N - 1}^{n}{{\left( { - 1} \right)}^{n}}\left( \begin{array}{ll} \frac{{{e^{ - \frac{{\left( {n + 1} \right){\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{{a_{2}}{\gamma_{0}}}}}}}}{{\left( {n + 1} \right)}} - \sum\limits_{k = 0}^{\infty} {\frac{1}{{k!}}} {\left( { - \frac{{{\lambda_{1}}{\lambda_{3}}{\omega_{3}}{\gamma_{t}}}}{{{b_{2}}{\gamma_{0}}}}} \right)^{k}} \hfill \\ {\left( {n + 1} \right)^{k - 1}}\Gamma \left( {1 - k,\frac{{(n + 1){\lambda_{1}}{\omega_{2}}{\gamma_{t}}}}{{{a_{2}}{\gamma_{0}}}}} \right) \hfill \end{array} \right)} ,\,\,\,\,if\,{b_{1}} \geqslant {b_{2}}\left( {1 + {\gamma_{t}}} \right)\,} \end{array}} \right. \hfill \end{array} $$
(49)

By combining (48) and (49), we finish the proof for Eq. 37.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ha, DB., Nguyen, S. Outage Performance of Energy Harvesting DF Relaying NOMA Networks. Mobile Netw Appl 23, 1572–1585 (2018). https://doi.org/10.1007/s11036-017-0922-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11036-017-0922-x

Keywords

Search

Navigation