User-centric Clustering and Beamforming for Energy Efficiency Optimization in Cloud-RAN

Abstract

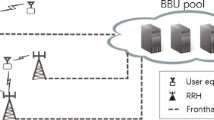
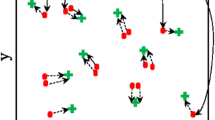
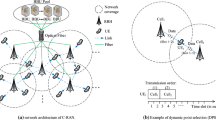
User-centric and energy efficient are becoming two foremost design principles in the cloud radio access networks (Cloud-RAN). In this paper, we thus consider the problem of how to assign each user to several preferred remote radio heads (RRHs) and design the corresponding beamforming coefficients in a user-centric and energy efficient manner. We formulate this problem as a joint clustering and beamforming optimization problem, with the objective to maximize the energy efficiency (EE) while satisfying the users’ quality of service (QoS) requirement and respecting the RRHs’ transmit power limits. We first transform it into an equivalent parametric subtractive problem using the approach in fractional programming, and then it is cast into a tractable convex optimization problem by introducing a lower bound of the objective function. Finally, the structure of the optimal solution is derived and a two-tier iterative scheme is developed to find the clustering pattern and beamforming coefficients that maximize EE. Specially, we derive a RRH-user association threshold, based on which the RRH clustering pattern and the corresponding beamforming coefficients can be simultaneously determined. Through simulations, we show the superior performance of the proposed user-centric clustering and beamforming scheme in Cloud-RAN.

Appendices

Appendix A: Proof of proposition 3

Define indicator function $I(\mathbf {v}) = \left \{ \begin {array}{llllll} 1\quad , & ~ \text {if } \mathbf {v} \in \mathcal {V}, \\ - \infty , & ~ \text {otherwise}. \end {array} \right .$. Then we can rewrite the problem P2 and P3 as the following unconstrained optimization problem respectively:

$$ \underset{\mathbf{v}} {\max} ~R_{sum}(\mathbf{v})-\theta P_{sum}(\mathbf{v}) + I(\mathbf{v}) \triangleq \underset{\mathbf{v}} {\max} ~ \mathcal{F}_{1}(\mathbf{v}), $$

(40)

$$ \underset{\mathbf{w}, \mathbf{u}, \mathbf{v}} {\max} ~ \mathcal{F}(\mathbf{w}, \mathbf{u}, \mathbf{v}) + I(\mathbf{v}) \triangleq \underset{\mathbf{w}, \mathbf{u}, \mathbf{v}} {\max} ~ \mathcal{F}_{2}(\mathbf{w}, \mathbf{u}, \mathbf{v}). $$

(41)

We can see that the smooth part of $\mathcal {F}_{1}(\mathbf {v}), \mathcal {F}_{2}(\mathbf {v})$ are differentiable, and the indicator function I(v) is separable across variables w,u and v. When other block variables are fixed, an unique optimal solution can be obtained. Combining these properties and applying Theorem 4.1 in [34], we can conclude that the proposed BCD method converges to a stationary solution of problem P3.

Furthermore, if (w^∗,u^∗,v^∗) is the stationary solution of problem (41), then based on Theorem 1, we have

$$ \begin{array}{lllllll} \mathcal{F}_{2}(\mathbf{w}^{*}, \mathbf{u}^{*}, \mathbf{v}^{*}) = &\mathcal{F}(\mathbf{w}^{*}, \mathbf{u}^{*}, \mathbf{v}^{*}) + I(\mathbf{v}^{*}) \\ = & \mathcal{F}_{1}(\mathbf{v}^{*}) \end{array} $$

(42)

Then using the stationary point definition and Danskin’s Theorem [28], we can obtain the following relationship

$$ \begin{array}{llllll} &\mathcal{F}_{2}^{\prime}(\mathbf{w}^{*}, \mathbf{u}^{*}, \mathbf{v}^{*} ; (0, \ldots, \mathbf{d}_{\mathbf{v}_{k}}, 0, \ldots, 0)) \\ & = \mathcal{F}_{1}^{\prime}(\mathbf{v}^{*} ; (0, \ldots, \mathbf{d}_{\mathbf{v}_{k}}, 0, \ldots, 0)) \geq 0, \forall \mathbf{d}_{\mathbf{v}_{k}}, \forall k \in \mathcal{K}, \end{array} $$

(43)

where $(0, \ldots , \mathbf {d}_{\mathbf {v}_{k}}, 0, \ldots , 0)$ is a vector of zero entries except for the block corresponding to the variable v _k with value $\mathbf {d}_{\mathbf {v}_{k}}$, and f^′(x^∗; d) is defined as the directional derivative of function f(⋅) at point x^∗ in the direction d, which can be calculated by $f^{\prime }(\mathbf {x}^{*}; \mathbf {d}) = \lim \inf _{\lambda \downarrow 0} \left [ f(\mathbf {x}^{*} + \lambda \mathbf {d}) - f(\mathbf {x}^{*}) \right ] /\lambda$. Hence, according to Eq. 43, v^∗ is also a stationary point of problem P2.

Appendix B: Proof of proposition 4

Define $\mathbf {D}_{mk}(c_{mk})\triangleq \frac { \mathbf {A}_{m}+\mathbf {B}_{mk}+ \left (\frac { \alpha _{k} p_{c} \theta c_{mk} }{2}+\theta \xi +\mu _{m} \right ) \mathbf {I}_{N} }{c_{mk}}$ , and rewrite the function as $\varphi (c_{mk}) = \left \|w_{k} u_{k} \mathbf {D}_{mk}^{-1}(c_{mk}) \mathbf {h}_{mk}\right \|_{2}$

$$\begin{array}{@{}rcl@{}} \frac{\partial \varphi (c_{mk}) }{\partial c_{mk}} &=& \frac{c_{mk} w_{k} \left\| u_{k} \right\|_{2} }{2} \left\| \mathbf{D}_{mk}^{-1}(c_{mk}) \mathbf{h}_{mk}\right\|_{2}^{-1} \\&&\times \frac{\partial }{\partial c_{mk}} \text{Tr}\left[ \mathbf{D}_{mk}^{-1}(c_{mk}) \mathbf{h}_{mk}\mathbf{h}_{mk}^{H} \mathbf{D}_{mk}^{-H}(c_{mk}) \right] \\ &=&\frac{w_{k} \left\| u_{k} \right\|_{2} }{c_{mk} } \left\| \mathbf{D}_{mk}^{-1}(c_{mk}) \mathbf{h}_{mk}\right\|_{2}^{-1} \\&&\times \text{Tr} \left[ \mathbf{D}_{mk}^{-1}(c_{mk}) \left( \mathbf{A}_{m}+\mathbf{B}_{mk}+ \left( \theta \xi +\mu_{m} \right) \mathbf{I}_{N} \right)\right.\\&&\times\left.\mathbf{D}_{mk}^{-1}(c_{mk}) \mathbf{h}_{mk}\mathbf{h}_{mk}^{H} \mathbf{D}_{mk}^{-H}(c_{mk}) \right] \end{array} $$

(44)

Since c _{m k} > 0, A _m , B _{m k} , D _{m k} (c _{m k} ) and $\mathbf {h}_{mk}\mathbf {h}_{mk}^{H}$ all are positive semi-definite, we have $\frac {\partial \varphi (c_{mk}) }{\partial c_{mk}} > 0$. Therefore φ(c _{m k} ) is a strictly increasing function of c _{m k} .