Skip to main content
SpringerLink
Log in

Security Performance Analysis of Underlay Cognitive Networks with Helpful Jammer Under Interference from Primary Transmitter

  • Published:
Mobile Networks and Applications Aims and scope Submit manuscript

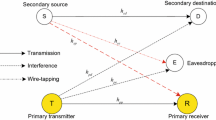
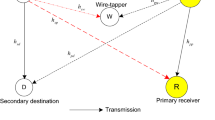
Abstract

Interference from primary transmitters in underlay cognitive networks is practically neither neglected nor integrated into noise terms although most literature inversely addressed. This paper firstly employs a helpful jammer to secure information transmission of a secondary transmitter. Then, its efficacy through secrecy outage probability under practical considerations consisting of exponentially distributed interference from primary transmitter, peak transmission power limitation, interference power limitation, and Rayleigh fading channels are analytically assessed. Finally, results are provided to illustrate significant security performance improvement thanks to exploiting the jammer while considerable security performance degradation due to interference from primary transmitter.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. This can be alternatively interpreted that jamming signal is transmitted in the null space to SD or shared with SD (e.g., use the seed of the jamming signal generator in a secure manner). Such interpretations are widely accepted in open literature (e.g., [17,18,19,20, 22, 27,28,29] and references therein).

References

  1. Panwar N, Sharma S, Singh AK (2016) A survey on 5G: the next generation of mobile communication. Elsevier Physical Communication 18(2):64–84

    Article  Google Scholar 

  2. Tavana M, Rahmati A, Shah-Mansouri V, Maham B (2017) Cooperative sensing with joint energy and correlation detection in cognitive radio networks. IEEE Commun Lett 21(1):132–135

    Article  Google Scholar 

  3. Ho-Van K (2016) Exact outage probability analysis of proactive relay selection in cognitive radio networks with MRC receivers. IEEE/KICS Journal of Communications and Networks 18(3):288–298

    Article  Google Scholar 

  4. Darsena D, Gelli G, Verde F (2017) An opportunistic spectrum access scheme for multicarrier cognitive sensor networks. IEEE Sensors J 17(8):2596–2606

    Article  Google Scholar 

  5. Liu Y, Chen H, Wang L (2017) Physical layer security for next generation wireless networks: theories, technologies, and challenges. IEEE Commun Surv Tutorials 19(1):347–376. First Quarter

    Article  Google Scholar 

  6. Sharma R, Rawat D (2015) Advances on security threats and countermeasures for cognitive radio networks: a survey. IEEE Commun Surv Tutorials 17(2):1023–1043

    Article  Google Scholar 

  7. Gan Z, Li-Chia C, Kai-Kit W (2011) Optimal cooperative jamming to enhance physical layer security using relays. IEEE Trans Sig Processing 59(3):1317–1322

    Article  MathSciNet  Google Scholar 

  8. Zhihui S, Yi Q, Song C (2013) On physical layer security for cognitive radio networks. IEEE Netw 27:28–33

    Article  Google Scholar 

  9. Yulong Z, Jia Z, Liuqing Y, Ying-chang L, Yu-dong Y (2015) Securing physical-layer communications for cognitive radio networks. IEEE Commun Mag 53:48–54

    Google Scholar 

  10. Li J, Feng Z, Feng Z, Zhang P (2015) A survey of security issues in cognitive radio networks. China Communications 12:132– 150

    Article  Google Scholar 

  11. Zheng TX, Wang HM (2016) Optimal power allocation for artificial noise under imperfect CSI against spatially random eavesdroppers. IEEE Trans Veh Tech 65(10):8812–8817

    Article  Google Scholar 

  12. Hu J, Cai Y, Yang N, Zhou X, Yang W (2017) Artificial-noise-aided secure transmission scheme with limited training and feedback overhead. IEEE Trans Wire Commun 16(1):193–205

    Article  Google Scholar 

  13. Wang C, Wang HM (2014) On the secrecy throughput maximization for MISO cognitive radio network in slow fading channels. IEEE Trans Inf Forensics Secur 9(11):1814–1827

    Article  Google Scholar 

  14. Ho-Van K (2015) Outage analysis in cooperative cognitive networks with opportunistic relay selection under imperfect channel information. Int J Electron Commun 69(11):1700–1708

    Article  Google Scholar 

  15. Wang D, Ren P, Du Q, Sun L, Wang Y (2016) Cooperative relaying and jamming for primary secure communication in cognitive two-way networks. In: Proceedings of IEEE VTC. Nanjing, China, pp 1–5

  16. Fang B, Qian Z, Zhong W, Shao W (2015) AN-Aided secrecy precoding for SWIPT in cognitive MIMO broadcast channels. IEEE Commun Lett 19(9):1632–1635

    Article  Google Scholar 

  17. Nguyen VD, Duong TQ, Dobre OA, Shin OS (2016) Joint information and jamming beamforming for secrecy rate maximization in cognitive radio networks. IEEE Trans Inf Forensics Secur 11(11):2609–2623

    Article  Google Scholar 

  18. Fang B, Qian Z, Shao W, Zhong W (2016) Precoding and artificial noise design for cognitive MIMOME wiretap channels. IEEE Trans Veh Tech 65(8):6753–6758

    Article  Google Scholar 

  19. Wu Y, Chen X, Chen X (2015) Secure beamforming for cognitive radio networks with artificial noise. In: Proceedings of IEEE WCSP. Nanjing, China, pp 1–5

  20. Hu X, Zhang X, Huang H, Li Y (2016) Secure transmission via jamming in cognitive radio networks with possion spatially distributed eavesdroppers. In: Proceedings of IEEE PIMRC. Valencia, Spain, pp 1–6

  21. Cai Y, Xu X, Yang W (2016) Secure transmission in the random cognitive radio networks with secrecy guard zone and artificial noise. IET Commun. 10(15):1904–1913

    Article  Google Scholar 

  22. Li Z, Jing T, Cheng X, Huo Y, Zhou W, Chen D (2015) Cooperative jamming for secure communications in MIMO cooperative cgnitive radio networks. In: Proceedings of IEEE ICC. London, UK, pp 7609–7614

  23. Liu W, Guo L, Kang T, Zhang J, Lin J (2015) Secure cognitive radio system with cooperative secondary networks. In: Proceedings IEEE ICT. Sydney, Australia, pp 6–10

  24. He T, Chen H, Liu Q (2013) Qos-based beamforming with cooperative jamming in cognitive radio networks. In: Proceedings of ICCCAS. Chengdu, China, pp 42–45

  25. Liu W, Sarkar MZI, Ratnarajah T (2014) On the security of cognitive radio networks: cooperative jamming with relay selection. In: Proceedings of EUCNC. Bologna, Italy, pp 1–5

  26. Liu W, Sarkar MZI, Ratnarajah T, Du H (2017) Securing cognitive radio with a combined approach of beamforming and cooperative jamming. IET Commun 11(1):1–9

    Article  Google Scholar 

  27. Zou Y (2017) Physical-layer security for spectrum sharing systems. IEEE Trans Wire Commun 16(2):1319–1329

    Article  Google Scholar 

  28. Liu Y, Wang L, Duy TT, Elkashlan M, Duong TQ (2015) Relay selection for security enhancement in cognitive relay networks. IEEE Wire Commun Lett 4(1):46–49

    Article  Google Scholar 

  29. Chakraborty P, Prakriya S (2017) Secrecy performance of an idle receiver assisted underlay secondary network. IEEE Trans Veh Tech 66(10):9555–9560

    Article  Google Scholar 

  30. Ho-Van K, Sofotasios PC, Freear S (2014) Underlay cooperative cognitive networks with imperfect Nakagami-m fading channel information and strict transmit power constraint: interference statistics and outage probability analysis. IEEE/KICS Journal of Communications and Networks 16(1):10–17

    Article  Google Scholar 

  31. Biglieri E, Proakis J, Shamai S (1998) Fading channels: information-theoretic and communications aspects. IEEE Trans Inf Theory 44(6):2619–2692

    Article  MathSciNet  Google Scholar 

  32. Wyner AD (1975) The wire-tap channel. Bell Syst Tech Journ 54(8):1355–1387

    Article  MathSciNet  Google Scholar 

  33. Gradshteyn IS, Ryzhik IM (2000) Table of integrals, series and products, 6th edn. Academic, San Diego

    MATH  Google Scholar 

  34. Zou Y, Wang X, Shen W (2013) Physical-layer security with multiuser scheduling in cognitive radio networks. IEEE Trans Commun 61(12):5103–5113

    Article  Google Scholar 

  35. Ahmed N, Khojastepour M, Aazhang B (2004) Outage minimization and optimal power control for the fading relay channel. In: Proceedings of IEEE information theory workshop. San Antonio, pp 458–462

  36. Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in C: the art of scientific computing, 2nd edn. Cambridge University Press, Cambridge

    MATH  Google Scholar 

Download references

Acknowledgements

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 102.04-2017.01

Author information

Authors and Affiliations

  1. Ho Chi Minh City University of Technology, VNU-HCM, 268 Ly Thuong Kiet Str., Dist. 10, Ho Chi Minh City, Vietnam

    Khuong Ho-Van & Thiem Do-Dac

  2. Thu Dau Mot University, 6 Tran Van On Str., Phu Hoa Ward, Thu Dau Mot City, Binh Duong Province, Vietnam

    Thiem Do-Dac

Authors
  1. Khuong Ho-Van
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thiem Do-Dac
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Khuong Ho-Van.

Appendices

Appendix A: Proof of Lemma 1

The conditional CDF of γd given Es is defined as

$$ {F_{{\gamma_{d}}}}\left( {\left. x \right|{E_{s}}} \right) = \Pr \left\{ {\left. {{\gamma_{d}} \le x} \right|{E_{s}}} \right\}. $$
(43)

Plugging (3) into (43) and performing some algebraic manipulations, one obtains

$$ \begin{array}{ll} &{F_{{\gamma_{d}}}}\left( {\left. x \right|{E_{s}}} \right) = \Pr \left\{ {\left. {\frac{{{E_{s}}{{\left| {{g_{sd}}} \right|}^{2}}}}{{{E_{p}}{{\left| {{g_{pd}}} \right|}^{2}} + {\sigma^{2}}}} \le x} \right|{E_{s}}} \right\} \\ &= \Pr \left\{ {\left. {{{\left| {{g_{sd}}} \right|}^{2}} \le \frac{{x\left( {{E_{p}}{{\left| {{g_{pd}}} \right|}^{2}} + {\sigma^{2}}} \right)}}{{{E_{s}}}}} \right|{E_{s}}} \right\}\\ &= {{\Xi}_{{{\left| {{g_{pd}}} \right|}^{2}}}}\!\left\{ {\Pr \!\left\{ {\left. {{{\!\left| {{g_{sd}}} \right|}^{2}} \!\le \frac{x}{{{E_{s}}}}\!\left( {{\!E_{p}}{{\left| {{g_{pd}}} \right|}^{2}} \!+ {\sigma^{2}}} \right)} \!\right|{{\left| {{g_{pd}}} \right|}^{2}},{E_{s}}} \!\right\}} \right\}\!. \end{array} $$
(44)

Due to \({g_{\texttt {tr}}} \sim \mathcal {C}\mathcal {N}\left ({0,{\alpha _{\texttt {tr}}}} \right )\), |gtr|2 follows the exponential distribution. Therefore, its CDF and PDF are respectively given by \({F_{{{\left | {{g_{\texttt {tr}}}} \right |}^{2}}}}\left (x \right ) = 1 - {e^{- x/{\alpha _{\texttt {tr}}}}}\) and \({f_{{{\left | {{g_{\texttt {tr}}}} \right |}^{2}}}}\left (x \right ) = {e^{- x/{\alpha _{\texttt {tr}}}}}/{\alpha _{\texttt {tr}}}\), x ≥ 0. Given this fact, one can simplify Eq. 44 as

$$ \begin{array}{ll} {F_{{\gamma_{d}}}}\!\left( {\left. x \right|{E_{s}}} \right) \!\!&=\! {{\Xi}_{{{\left| {{g_{pd}}} \right|}^{2}}}}\!\left\{ {\!1 - \left. {{e^{- \frac{x}{{{E_{s}}{\alpha_{sd}}}}\left( {{E_{p}}{{\left| {{g_{pd}}} \right|}^{2}} + {\sigma^{2}}} \right)}}} \!\right|\!{{\left| {{g_{pd}}} \right|}^{2}}\!,\!{E_{s}}} \right\} \\ &= 1 - \int\limits_{0}^{\infty} {{e^{- \frac{x}{{{E_{s}}{\alpha_{sd}}}}\left( {{E_{p}}y + {\sigma^{2}}} \right)}}{f_{{{\left| {{g_{pd}}} \right|}^{2}}}}\left( y \right)dy} \\ &= 1 - \int\limits_{0}^{\infty} {{e^{- \frac{x}{{{E_{s}}{\alpha_{sd}}}}\left( {{E_{p}}y + {\sigma^{2}}} \right)}}\frac{1}{{{\lambda_{pd}}}}{e^{- \frac{y}{{{\lambda_{pd}}}}}}dy} \\ &= 1 - {\left( {\frac{{{E_{p}}{\alpha_{pd}}x}}{{{E_{s}}{\alpha_{sd}}}} + 1} \right)^{- 1}}{e^{- \frac{{x{\sigma^{2}}}}{{{E_{s}}{\alpha_{sd}}}}}}. \end{array} $$
(45)

Taking the derivative of \({F_{{\gamma _d}}}\left ({\left . x \right |{E_{s}}} \right )\) with respect to x, simplifying the result and using compact notations in Eqs. 23, 24, 25, one obtains \({f_{{\gamma _d}}}\left ({\left . x \right |{E_{s}}} \right ) = \frac {d}{{dx}}{F_{\gamma _{d}}}\left ({\left . x \right |{E_{s}}} \right )\) as exactly shown in Eq. 22, completing the proof.

Appendix B: Proof of Lemma 2

The conditional CDF of γw given Es according to its definition is

$$ {F_{{\gamma_{w}}}}\left( {\left. x \right|{E_{s}}} \right) = \Pr \left\{ {\left. {{\gamma_{w}} \le x} \right|{E_{s}}} \right\}. $$
(46)

Plugging Eq. 4 into Eq. 46 and performing some algebraic manipulations, one obtains

$$ \begin{array}{ll} &{F_{{\gamma_{w}}}}\left( {\left. x \right|{E_{s}}} \right) = \Pr \left\{ {\left. {\frac{{{E_{s}}{{\left| {{g_{sw}}} \right|}^{2}}}}{{{E_{j}}{{\left| {{g_{jw}}} \right|}^{2}} + {E_{p}}{{\left| {{g_{pw}}} \right|}^{2}} + {\sigma^{2}}}} \le x} \right|{E_{s}}} \right\} \\ &= \Pr \left\{ {\left. {{{\left| {{g_{sw}}} \right|}^{2}} \le \frac{x}{{{E_{s}}}}\left( {{E_{j}}{{\left| {{g_{jw}}} \right|}^{2}} + {E_{p}}{{\left| {{g_{pw}}} \right|}^{2}} + {\sigma^{2}}} \right)} \right|{E_{s}}} \right\} \\ &= {{\Xi}_{{{\left| {{g_{jp}}} \right|}^{2}},{{\left| {{g_{jw}}} \right|}^{2}},{{\left| {{g_{pw}}} \right|}^{2}}}}\!\left\{ {\!1 - \left. {{e^{- \frac{{x\left( {{E_{j}}{{\left| {{g_{jw}}} \right|}^{2}} + {E_{p}}{{\left| {{g_{pw}}} \right|}^{2}} + {\sigma^{2}}} \right)}}{{{E_{s}}{\alpha_{sw}}}}}}} \right|{E_{s}}} \right\} \\ &= 1 - {e^{- \frac{{x{\sigma^{2}}}}{{{E_{s}}{\alpha_{sw}}}}}}\underbrace {{{\Xi}_{{{\left| {{g_{pw}}} \right|}^{2}}}}\left\{ {{e^{- \frac{{x{E_{p}}}}{{{E_{s}}{\alpha_{sw}}}}{{\left| {{g_{pw}}} \right|}^{2}}}}} \right\}}_{\mu} \times \\ &\underbrace {{{\Xi}_{{{\left| {{g_{jp}}} \right|}^{2}}}}\left\{ {\left. {\underbrace {{{\Xi}_{{{\left| {{g_{jw}}} \right|}^{2}}}}\left\{ {\left. {{e^{- \frac{{x{E_{j}}}}{{{E_{s}}{\alpha_{sw}}}}{{\left| {{g_{jw}}} \right|}^{2}}}}} \right|{E_{s}}} \right\}}_{\kappa} } \right|{E_{s}}} \right\}}_{\zeta}. \end{array} $$
(47)

Quantities (κ, μ, ζ) are computed as follows. First of all, κ can be expressed in closed-form as

$$ \begin{array}{ll} \kappa &= {{\Xi}_{{{\left| {{g_{jw}}} \right|}^{2}}}}\left\{ {\left. {{e^{- \frac{{x{E_{j}}}}{{{E_{s}}{\alpha_{sw}}}}{{\left| {{g_{jw}}} \right|}^{2}}}}} \right|{E_{s}}} \right\} \\ &= \int\limits_{0}^{\infty} {{e^{- \frac{{x{E_{j}}}}{{{E_{s}}{\alpha_{sw}}}}y}}{f_{{{\left| {{g_{jw}}} \right|}^{2}}}}\left( y \right)dy} \\ &= \int\limits_{0}^{\infty} {{e^{- \frac{{x{E_{j}}}}{{{E_{s}}{\alpha_{sw}}}}y}}\frac{1}{{{\alpha_{jw}}}}{e^{- \frac{y}{{{\alpha_{jw}}}}}}dy} \\ &= {\left( {\frac{{x{E_{j}}{\alpha_{jw}}}}{{{E_{s}}{\alpha_{sw}}}} + 1} \right)^{- 1}}. \end{array} $$
(48)

Imitating the procedure of deriving κ, one can straightforwardly infer that

$$ \mu = {\left( {\frac{{x{E_{p}}{\alpha_{pw}}}}{{{E_{s}}{\alpha_{sw}}}} + 1} \right)^{- 1}}. $$
(49)

By inserting Eq. 14 into Eq. 48 and then statistically averaging the result over a random variable |gjp|2, one obtains the exact closed form of ζ as

$$ \begin{array}{ll} \zeta &= {{\Xi}_{{{\left| {{g_{jp}}} \right|}^{2}}}}\left\{ {{{\left[ {\frac{{x{\alpha_{jw}}}}{{{E_{s}}{\alpha_{sw}}}}\min \left( {\frac{T}{{2{{\left| {{g_{jp}}} \right|}^{2}}}},{{\tilde E}_{j}}} \right) + 1} \right]}^{- 1}}} \right\} \\ &= \underbrace {\int\limits_{0}^{\frac{T}{{2{{\tilde E}_{j}}}}} {{{\left( {\frac{{x{\alpha_{jw}}{{\tilde E}_{j}}}}{{{E_{s}}{\alpha_{sw}}}} + 1} \right)}^{- 1}}{f_{{{\left| {{g_{jp}}} \right|}^{2}}}}\left( y \right)dy} }_{\tilde \zeta } \\ &+ \underbrace {\int\limits_{\frac{T}{{2{{\tilde E}_{j}}}}}^{\infty} {{{\left( {\frac{{x{\alpha_{jw}}}}{{{E_{s}}{\alpha_{sw}}}}\frac{T}{{2y}} + 1} \right)}^{- 1}}{f_{{{\left| {{g_{jp}}} \right|}^{2}}}}\left( y \right)dy} }_{\bar \zeta } \end{array} $$
(50)

The first term in Eq. 50 is easily solved as

$$ \tilde \zeta = {\left( {\frac{{x{\alpha_{jw}}{{\tilde E}_{j}}}}{{{E_{s}}{\alpha_{sw}}}} + 1} \right)^{- 1}}\left( {1 - {e^{- \frac{T}{{2{{\tilde E}_{j}}{\alpha_{jp}}}}}}} \right). $$
(51)

while the second term is further simplified as

$$ \begin{array}{ll} \bar \zeta &= \int\limits_{\frac{T}{{2{{\tilde E}_{j}}}}}^{\infty} {\left[ {1 - \frac{{x{\alpha_{jw}}T}}{{2{E_{s}}{\alpha_{sw}}}}{{\left( {y + \frac{{x{\alpha_{jw}}T}}{{2{E_{s}}{\alpha_{sw}}}}} \right)}^{- 1}}} \right]\frac{1}{{{\alpha_{jp}}}}{e^{- \frac{y}{{{\alpha_{jp}}}}}}dy} \\ &= \int\limits_{\frac{T}{{2{{\tilde E}_{j}}}}}^{\infty} {\frac{1}{{{\alpha_{jp}}}}{e^{- \frac{y}{{{\alpha_{jp}}}}}}dy - \frac{{x{\alpha_{jw}}T}}{{2{E_{s}}{\alpha_{sw}}{\alpha_{jp}}}}\int\limits_{\frac{T}{{2{{\tilde E}_{j}}}}}^{\infty} {\frac{{{e^{- \frac{y}{{{\alpha_{jp}}}}}}}}{{y + \frac{{x{\alpha_{jw}}T}}{{2{E_{s}}{\alpha_{sw}}}}}}dy} }. \end{array} $$
(52)

The first integrand in Eq. 52 is easily computed and the second one can be expressed in terms of the Ei(⋅) function, resulting in

$$ \begin{array}{ll} &\bar \zeta = {e^{- \frac{T}{{2{{\tilde E}_{j}}{\alpha_{jp}}}}}} \\ &+ \frac{{x{\alpha_{jw}}T}}{{2{E_{s}}{\alpha_{sw}}{\alpha_{jp}}}}{e^{\frac{{x{\alpha_{jw}}T}}{{2{E_{s}}{\alpha_{sw}}{\alpha_{jp}}}}}}Ei\left( { - \frac{T}{{2{{\tilde E}_{j}}{\alpha_{jp}}}} - \frac{{x{\alpha_{jw}}T}}{{2{E_{s}}{\alpha_{sw}}{\alpha_{jp}}}}} \right). \end{array} $$
(53)

Plugging Eqs. 51 and 53 into Eq. 50 and then inserting the result together with Eq. 49 into Eq. 47, one can reduce Eqs. 47 to 26 after using notations in Eqs. 27, 28, 29, 30, 31. This finishes the proof of Lemma 2.

Appendix C: Closed-form representations of some special integrands

Start with the integrand in Eq. 36. By changing variable y = x + b and then applying the definition of the Ei(⋅) function, the closed-form representation of Eq. 36 is

$$ \mathcal{J}\left( {a,b} \right) = - {e^{ab}}Ei\left( { - ab} \right). $$
(54)

Performing the integral by part to Eq. 37 and then using the result of Eq. 54, the closed-form representation of Eq. 37 is

$$ \begin{array}{ll} \mathcal{F}\left( {a,b} \right) &= \frac{1}{b} - a\int\limits_{0}^{\infty} {\frac{{{e^{- ax}}}}{{x + b}}dx} \\ &= \frac{1}{b} + a{e^{ab}}Ei\left( { - ab} \right). \end{array} $$
(55)

By using the approximation of the Ei(⋅) function in [36, Eq. (6.3.11)] as \(Ei\left (x \right ) \approx \frac {{{e^x}}}{x}\), one can obtain the closed form of Eq. 38 after some algebraic manipulations as

$$ \begin{array}{ll} \mathcal{M}\left( {b,c,g,l} \right) &\approx \int\limits_{0}^{\infty} {\frac{{{e^{- bx}}}}{{x + c}}\frac{{{e^{- gx - l}}}}{{ - gx - l}}dx} \\ &=- \frac{{{e^{- l}}}}{g}\left[ {\frac{1}{{l/g - c}}\int\limits_{0}^{\infty} {\frac{{{e^{- \left( {b + g} \right)x}}}}{{x + c}}dx} } \right. \\ &+ \left. {\frac{1}{{c - l/g}}\int\limits_{0}^{\infty} {\frac{{{e^{- \left( {b + g} \right)x}}}}{{x + l/g}}dx} } \right] \\ &=\frac{{{e^{bl/g}}}}{{cg - l}}Ei\left( { - \frac{{\left[ {b + g} \right]l}}{g}} \right) \\ &- \frac{{{e^{\left( {b + g} \right)c - l}}}}{{cg - l}}Ei\left( { - \left[ {b + g} \right]c} \right). \end{array} $$
(56)

It is noted that the integrands in the second equality of Eq. 56 are obtained with the help of Eq. 54.

Again using the approximation of the Ei(⋅) function as \(Ei\left (x \right ) \approx \frac {{{e^x}}}{x}\), one can simplify (39) as

$$ \mathcal{Y}\left( {b,c,g,l} \right) \approx \int\limits_{0}^{\infty} {\frac{{{e^{- bx}}}}{{{{\left( {x + c} \right)}^{2}}}}\frac{{{e^{- gx - l}}}}{{ - gx - l}}dx}. $$
(57)

Performing the partial fraction decomposition to \(\frac {1}{{{{\left ({x + c} \right )}^{2}}\left ({x + l/g} \right )}}\), one represents (57) in a more compact form as

$$ \begin{array}{ll} \mathcal{Y}\left( {b,c,g,l} \right) &= - \frac{{{e^{- l}}}}{g}\left( {\frac{1}{{l/g - c}}\int\limits_{0}^{\infty} {\frac{{{e^{- \left( {b + g} \right)x}}}}{{{{\left( {x + c} \right)}^{2}}}}dx} } \right. \\ &- \frac{1}{{{{\left( {c - l/g} \right)}^{2}}}}\int\limits_{0}^{\infty} {\frac{{{e^{- \left( {b + g} \right)x}}}}{{x + c}}dx} \\ &+ \left. {\frac{1}{{{{\left( {c - l/g} \right)}^{2}}}}\int\limits_{0}^{\infty} {\frac{{{e^{- \left( {b + g} \right)x}}}}{{x + l/g}}dx} } \right). \end{array} $$
(58)

Finally, exploiting the results in Eqs. 54 and 55, the closed-form representation of Eq. 39 is

$$ \begin{array}{ll} \mathcal{Y}\left( {b,c,g,l} \right) &= \frac{g} {{(l - cg)}^{2}} {e^{bl/g}}Ei\left( { - \frac{{\left[ {b + g} \right]l}}{g}} \right) - \frac{{{e^{- l}}}}{{\left( {l - cg} \right)c}} \\ &- \frac{e^{\left( {b + g} \right)c - l}} {{l - cg}}\left( {b + g + \frac{g}{{l - cg}}} \right)Ei\left( { - \left[ {b + g} \right]c} \right). \end{array} $$
(59)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ho-Van, K., Do-Dac, T. Security Performance Analysis of Underlay Cognitive Networks with Helpful Jammer Under Interference from Primary Transmitter. Mobile Netw Appl 25, 4–15 (2020). https://doi.org/10.1007/s11036-018-1185-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11036-018-1185-x

Keywords

Search

Navigation