Abstract
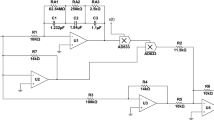
In this paper, a new fractional-order memristive circuit is defined based on canonical Chua’s circuit and Voltage-controlled memristor model. The fractional-order chaotic system is solved by conformable Adomian decomposition method (CADM), and the complexity characteristics are analyzed through sample entropy (SampEn) algorithm. The complexity analysis results correspond to the bifurcation diagram and Lyapunov exponential spectrum, which shows that SampEn algorithm can effectively reflects complexity of chaotic system. What’s more, the chaos diagrams of complexity with the two parameters variation and the three parameters variation are analyzed. The numerical simulation result indicates that the system parameters variable complexity can effectively reflect the randomness of the fractional-order chaotic system, and the system has rich dynamical performances. It provides the theoretical guidance and experimental evidence for fractional-order memristive chaotic circuit application in cryptography and secure communication.








Similar content being viewed by others
References
Chua LO (1971) Memristor-the missing circuit element[J]. IEEE Trans Circuit Theory 18(5):507–519
Strukov DB, Snider GS, Stewart DR et al (2008) The missing memristor found[J]. Nature 453(7191):80–83
Chua L (2011) Resistance switching memories are memristors[J]. Appl Phys A Mater Sci Process 102(4):765–783
Si G, Diao L, Zhu J (2016) Fractional-order charge-controlled memristor: theoretical analysis and simulation[J]. Nonlinear Dynamics, 2016 87(4):1–10
Ye X, Mou J, Luo C et al (2018) Dynamics analysis of Wien-bridge hyperchaotic memristive circuit system[J]. Nonlinear Dynamics 92(3):1–11
Tan Q, Zeng Y, Li Z (2018) A simple inductor-free memristive circuit with three line equilibria[J]. Nonlinear Dynamics 2018(6):1–18
Sun J, Zhao X, Fang J, et al. (2018) Autonomous memristor chaotic systems of infinite chaotic attractors and circuitry realization[J]. Nonlinear Dynamics: 1-9
Ruan J, Sun K, Mou J et al (2018) Fractional-order simplest memristor-based chaotic circuit with new derivative[J]. European Physical Journal Plus 133(1):3
Bao B, Wang N, Xu Q et al (2017) A simple third-order Memristive band pass filter chaotic circuit[J]. IEEE Transactions on Circuits & Systems II Express Briefs 64(8):977–981
Li C, Chen et al (2004) Chaos and hyperchaos in the fractional-order Rössler equations[J]. Physica A Statistical Mechanics & Its Applications 341(1–4):55–61
Sun H, Charef A, Tsao YY et al (1992) Analysis of polarization dynamics by singularity decomposition method[J]. Ann Biomed Eng 20(3):321
Khodabakhshi N, Vaezpour SM, Baleanu D (2014) Numerical solutions of the initial value problem for fractional differential equations by modification of the Adomian decomposition method[J]. Fractional Calculus & Applied Analysis 17(2):382–400
Arasteh D (2008) Measures of order in dynamic systems[J]. J Comput Nonlinear Dyn 3(3):635–644
Ye X, Mou J, Luo C et al (2018) Complexity analysis of a mixed Memristive chaotic circuit[J]. Complexity 2018:1–9
Shaobo H, Kehui S, Huihai W (2016) Modified multiscale permutation entropy algorithm and its application for multiscroll chaotic systems[J]. Complexity 21(5):52–58
Balasubramanian K, Nair SS, Nagaraj N (2015) Classification of periodic, chaotic and random sequences using approximate entropy and Lempel–Ziv complexity measures[J]. Pramana 84(3):1–8
Sun KH, Shao-Bo HE, Zhu CX et al (2013) Analysis of chaotic complexity characteristics based on C_0 algorithm[J]. Acta Electron Sin 41(9):1765–1771
Khalil R, Horani MA, Yousef A et al (2014) A new definition of fractional derivative[J]. J Comput Appl Math 264(5):65–70
Chung WS (2015) Fractional Newton mechanics with conformable fractional derivative[J]. J Comput Appl Math 290(C):150–158
Yan W, Sun K, He S et al (2014) Dynamics of fractional-order sinusoidally forced simplified Lorenz system and its synchronization[J]. European Physical Journal Special Topics 223(8):1591–1600
He S, Sun K, Mei X et al (2017) Numerical analysis of a fractional-order chaotic system based on conformable fractional-order derivative[J]. European Physical Journal Plus 132(1):36
Xu Y, Sun K, He S et al (2016) Dynamics of a fractional-order simplified unified system based on the Adomian decomposition method[J]. European Physical Journal Plus 131(6):1–12
Wang H, Sun K, He S (2015) Characteristic Analysis and DSP Realization of Fractional-Order Simplified Lorenz System Based on Adomian Decomposition Method[J]. International Journal of Bifurcation and Chaos 25(6):1550085
Zhang L, Sun K, He S et al (2017) Solution and dynamics of a fractional-order 5-D hyperchaotic system with four wings[J]. European Physical Journal Plus 132(1):31
Richman JS, Lake DE, Moorman JR (2004) Sample entropy[J]. Methods Enzymol 384(384):172–184
Bao H, Jiang T, Chu K, et al (2018) Memristor-based canonical Chua’s circuit: extreme multistability in voltage-current domain and its controllability in flux-charge domain[J]. Complexity 5935637
Acknowledgements
This research is supported by the Basic Scientific Research Projects of Colleges and Universities of Liaoning Province (Grant No. 2017J046).
Author information
Authors and Affiliations
Contributions
Feifei Yang designed and carried out experiments, data analyzed and manuscript wrote. Peng Li made the theoretical guidance for this paper.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that we have no conflicts of interests about the publication of this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Yang, F., Li, P. Characteristics Analysis of the Fractional-Order Chaotic Memristive Circuit Based on Chua’s Circuit. Mobile Netw Appl 26, 1862–1870 (2021). https://doi.org/10.1007/s11036-019-01294-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11036-019-01294-8