Skip to main content
SpringerLink
Log in

A parallel image encryption method based on compressive sensing

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

Recently, compressive sensing-based encryption methods which combine sampling, compression and encryption together have been proposed. However, since the quantized measurement data obtained from linear dimension reduction projection directly serve as the encrypted image, the existing compressive sensing-based encryption methods fail to resist against the chosen-plaintext attack. To enhance the security, a block cipher structure consisting of scrambling, mixing, S-box and chaotic lattice XOR is designed to further encrypt the quantized measurement data. In particular, the proposed method works efficiently in the parallel computing environment. Moreover, a communication unit exchanges data among the multiple processors without collision. This collision-free property is equivalent to optimal diffusion. The experimental results demonstrate that the proposed encryption method not only achieves the remarkable confusion, diffusion and sensitivity but also outperforms the existing parallel image encryption methods with respect to the compressibility and the encryption speed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. Liao et al. [15] claimed that the full diffusion could be achieved even after the first round of encryption. However, their experiment in diffusion performance evaluation was not impartial. If one changes the original image pixel in the second quadrant, at least three rounds of encryption were necessary. Therefore, the property that full diffusion could be achieved after the first round encryption was just a best case. It should be bear in mind that when evaluating the security, only the worst boundary can be taken as a result.

  2. The necessary round is defined as the minimum round to achieve the full confusion and diffusion.

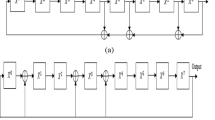
  3. Definition of unit throughput. Assume that the workload allocated to a processor is w, and the processing capacity of this processor is c. The unit throughput is defined as w/c.

  4. Here, (m, n) is the coordinate of a quantized measurement within a block, while coordinate printed in the bold font (m, n) stands for the position of a block.

References

  1. Babadi B, Kalouptsidis N, Tarokh V (2010) SPARLS: the sparse RLS algorithm. IEEE Trans Signal Process 58(8):4013–4025

    Article  MathSciNet  Google Scholar 

  2. Baraniuk RG (2007) Compressive sensing. IEEE Signal Process Mag 24(4):118–121

    Article  Google Scholar 

  3. Bioucas J, Figueiredo M (2007) A New TwIST: two-step iterative shrinkage thresholding algortihms for image restoration. IEEE Trans Image Process 16(12):2992–3004

    Article  MathSciNet  Google Scholar 

  4. Blumensath T, Davies ME (2008) Gradient pursuits. IEEE Trans Signal Process 56(6):2370–2382

    Article  MathSciNet  Google Scholar 

  5. Candès EJ, Tao T (2005) Decoding by linear programming. IEEE Trans Inf Theory 51(12):4203–4215

    Article  MATH  Google Scholar 

  6. Candès EJ, Romberg J, Tao T (2006) Robust uncertainty principles: exact signal reconstruction from highly incomplete frequecny information. IEEE Trans Inf Theory 52(2):489–509

    Article  MATH  Google Scholar 

  7. Donoho DL (2006) Compressive sensing. IEEE Trans Inf Theory 52(4):1289–1306

    Article  MATH  MathSciNet  Google Scholar 

  8. Fei P, Qiu SS, Min L (2005) An Image Encryption Algorithm based on Mixed Chaotic Dynamic Systems and External Keys. In IEEE Internation Conference Communic Circuits & Systems, pp: 1135–1139

  9. Gan L (2007) Block Compressed Sensing of Natural Images. In 15th International Conference on Digital Signal Processing, pp: 403–406

  10. Gang C, Yu ZX (2005) A self-adaptive algorithm on image encryption. J Softw 119(11):1974–1982

    Google Scholar 

  11. Gao DH, Liu DH, Feng YQ Yu FP (2010) A Robust Image Transmission Scheme for Wireless Channels Based on Compressive Sensing. In ICIC′10 Proceedings of the Advanced intelligent computing theories and applications, pp: 334–341

  12. Gorodnitsky IF, Rao BD (1997) Sparse signal reconstruction from limited data using FOCUSS: a re-weighted norm minmization algorithm. IEEE Trans Signal Process 45(3):600–616

    Article  Google Scholar 

  13. Grangetto M, Magli E, Olmo G (2006) Multimedia selective encryption by means of randomized arithmetic coding. IEEE Trans Multimed 8(5):905–917

    Article  Google Scholar 

  14. Lian SG (2008) Multimedia content encryption. CRC Press, Boca Raton

    MATH  Google Scholar 

  15. Liao XF, Lai SY, Zhou Q (2010) A novel image encryption algorithm based on self-adaptive wave transmission. Signal Process 90:2714–2722

    Article  MATH  Google Scholar 

  16. Liu DH, Shi GM, Gao DH, Gao M (2009) A Robust Image Encryption Scheme over Wireless Channels. In International Conference on Wireless Communications & Signal Processing, pp: 1–6

  17. Lloyd S (1982) Least squares quantization in PCM. IEEE Trans Inf Theory 28(2):129–137

    Article  MATH  MathSciNet  Google Scholar 

  18. Lustig M, Donoho DL, Santos JM, Pauly JM (2008) Compressed sensing MRI. IEEE Trans Signal Process 25(2):72–82

    Article  Google Scholar 

  19. Mastan JMK, Sathishkumar GA, Bagan KB (2011) A color image encryption technique based on a substitution-permutation network. Adv Comput Commun 193(5):524–533

    Article  Google Scholar 

  20. Mirzaei O, Yaghoobi M, Irani H (2011) A New image encryption method: parallel Sub-image encryption with hyper chaos. Nonlinear Dyn. doi:10.1007/s11071-011-0006-6

  21. Mollin RA (2006) An introduction to cryptography. CRC Press, Boca Raton

    Google Scholar 

  22. Olshausen BA, Field DJ (1997) Sparse coding with an overcomplete basis Set: a strategy employed by V1. Vis Res 37(23):3311–3325

    Article  Google Scholar 

  23. Orsdemir A, Altun HO, Sharma G, Bocko MF (2008) On the Security and Robustness of Encryption via Compressed Sensing. In IEEE Military Communications Conference, pp: 1–7

  24. Rachlin Y, Baron D (2008) The Secrecy of Compressed Sensing Measurements. In 46th Annual Allerton Conference on Communication, Control and Computing, September, pp: 813–817

  25. Shtewi AA, Hasan BEM, Hegazy AEF (2010) An efficient modified advanced encryption standard (MAES) adapted for image cryptosystems. Int J Comput Sci Netw Secur 10(2):226–232

    Google Scholar 

  26. Tropp JA, Gilbert AC (2007) Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans Inf Theory 53(12):4655–4666

    Article  MATH  MathSciNet  Google Scholar 

  27. Vanstone SA, Menezes AJ, Oorschot PC (1999) Handbook of applied cryptography. CRC Press, Boca Raton

    Google Scholar 

  28. Wang S, Kuang J, Li J (2002) Chaos-based communication in a large community. Phys Rev 66(6):1–4

    Article  MATH  Google Scholar 

  29. Wu CP, Kuo CCJ (2000) Fast Encryption Methods for Audiovisual Data Confidentiality. In Proceedings of SPIE, pp: 284–295

  30. Wu Y, Noonan JP, Agaian S (2011) NPCR and UACI randomness tests for image encryption. Cyber J: Multidiscip J Sci Technol: J Sel Areas Telecommun 2(4):31–38

    Google Scholar 

  31. Zhou K, Wong X, Liao F et al (2008) Parallel image encryption algorithm based on discretized chaotic Map. Chaos, Solitons Fractals 38:1081–1092

    Article  Google Scholar 

  32. Zhou Q, Hu Y, Liao XF (2010) Analysis of the diffusion property of image encryption algorithm in block-and-permutation mode and its implementation. J Electron Inf Technol (Chin) 32(8):2015–2018

    Article  Google Scholar 

Download references

Acknowledgment

The second author acknowledges the support provided by Grant NRF-2011-013-D00121 from the National Research Foundation of Korea.

Author information

Authors and Affiliations

  1. Graduate School of Information Science and Electrical Engineering, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka, Japan

    R. Huang, K. H. Rhee & S. Uchida

  2. Department of IT Convergence and Application Engineering, Pukyong National University, 599-1, Daeyeon 3-Dong, Nam-Gu, Busan, 608-737, South Korea

    K. H. Rhee

Authors
  1. R. Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. H. Rhee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Uchida
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. Huang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Huang, R., Rhee, K.H. & Uchida, S. A parallel image encryption method based on compressive sensing. Multimed Tools Appl 72, 71–93 (2014). https://doi.org/10.1007/s11042-012-1337-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-012-1337-0

Keywords

Search

Navigation