Skip to main content

Advertisement

Springer Nature Link
Log in

Active contour driven by multi-scale local binary fitting and Kullback-Leibler divergence for image segmentation

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

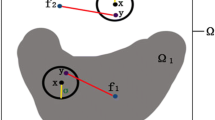
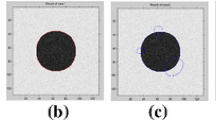
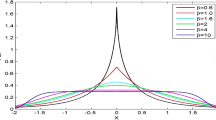
Image segmentation is an important processing in many applications such as image retrieval and computer vision. One of the most successful models for image segmentation is the level set methods which are based on local context. The methods, though comparatively effective in segmenting images with inhomogeneous intensity, are considerably computation-intensive and at the risk of falling into local minima in the convergence of the active contour energy function. To address the issues, we propose a region-based level set method, called KL-MLBF, which is based on the multi-scale local binary fitting (MLBF) and the Kullback-Leibler (KL) divergence. We first apply the multi-scale theory to the local binary fitting model to build MLBF. Then the energy term measured by KL divergence between regions to be segmented is incorporated into the energy function of MLBF. KL-MLBF utilizes the between-cluster distance and the adaptive kernel function selection strategy to formulate the energy function. Being more robust to the initial location of the contour than the classical segmentation models, KL-MLBF can deal with blurry boundaries and noise problems. The results of experiments on synthetic and real images have shown that KL-MLBF can improve the effectiveness of segmentation while ensuring the accuracy by accelerating the minimization of the energy function.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Balla-Arabé S, Gao X, Wang B (2013) A fast and robust level set method for image segmentation using fuzzy clustering and lattice boltzmann method. IEEE Transactions on Cybernetics 43(3):910– 920

    Article  Google Scholar 

  2. Candès E J, Li X, Ma Y, Wright J (2011) Robust principal component analysis?. J ACM (JACM) 58(3):11

    Article  MathSciNet  MATH  Google Scholar 

  3. Casselles F C V, Dibos F (1993) A geometric model for active contours in image processing. Numer Math 66(1):1–31

    Article  MathSciNet  MATH  Google Scholar 

  4. Cheng D, Huang J, Yu Z, Tang X, Yang J (2007) Medical image enhancement based on fuzzy techniques. Journal of Harbin Institute of Technology 39 (3):435–437

    Google Scholar 

  5. Cheng D, Liu X, Tang X, Liu J, Huang J (2007) An image segmentation method based on an improved pcnn [j]. Chinese High Technology Letters 12:24–29

    Google Scholar 

  6. Cohen L, Cohen I (1993) “Finite-element methods for active contour models and balloons for 2-d and 3-d images”. IEEE Trans Pattern Anal Mach Intell 15(11):1131–1147

    Article  Google Scholar 

  7. Gong M, Liang Y, Shi J, Ma W, Ma J (2013) Fuzzy c-means clustering with local information and kernel metric for image segmentation. IEEE Trans Image Process 22(2):573–584

    Article  MathSciNet  Google Scholar 

  8. Islam M J, Basalamah S, Ahmadi M, Sid-Ahmed M A (2011) “Capsule image segmentation in pharmaceutical applications using edge-based techniques”. In: Electro/Information Technology (EIT), 2011 IEEE International Conference on. IEEE, pp 1–5

  9. Kass M, Witkin A, Terzopoulos D (1988) Snakes: Active contour models. Int J Comput Vis 1(4):321–331

    Article  MATH  Google Scholar 

  10. Kullback S, Leibler R A (1951) On information and sufficiency. Ann Math Stat:79–86

  11. Lankton S, Tannenbaum A (2008) Localizing region-based active contours. IEEE Trans Image Process 17(11):2029–2039

  12. Leung T, Malik J (1998) “Contour continuity in region based image segmentation”. In: Computer VisionłECCV’98. Springer, pp 544–559

  13. Li C, Huang R, Ding Z, Gatenby J, Metaxas D N, Gore J C (2011) A level set method for image segmentation in the presence of intensity inhomogeneities with application to mri. IEEE Trans Image Process 20(7):2007–2016

    Article  MathSciNet  Google Scholar 

  14. Li C, Kao C. -Y., Gore J C, Ding Z (2007) “Implicit active contours driven by local binary fitting energy”. In: Computer Vision and Pattern Recognition, 2007. CVPR’07 IEEE Conference on. IEEE , pp 1–7

  15. Li C, Xu C, Gui C, Fox M D (2005) “Level set evolution without re-initialization: a new variational formulation”. In: Computer Vision and Pattern Recognition, 2005. CVPR 2005 IEEE Computer Society Conference on, vol. 1. IEEE, pp 430–436

  16. Li C, Xu C, Gui C, Fox M D (2010) Distance regularized level set evolution and its application to image segmentation. IEEE Trans Image Process 19(12):3243–3254

    Article  MathSciNet  Google Scholar 

  17. Liu S, Peng Y (2012) A local region-based chan–vese model for image segmentation. Pattern Recogn 45(7):2769–2779

    Article  MATH  Google Scholar 

  18. Liu T, Yuan Z, Sun J, Wang J, Zheng N, Tang X, Shum H -Y (2011) Learning to detect a salient object. IEEE Trans Pattern Anal Mach Intell 33 (2):353–367

    Article  Google Scholar 

  19. Mansouri A -R, Konrad J (2003) Multiple motion segmentation with level sets. IEEE Trans Image Process 12(2):201–220

    Article  Google Scholar 

  20. Malladi R, Sethian J A, Vemuri B C (1995) Shape modeling with front propagation: a level set approach. IEEE Trans Pattern Anal Mach Intell 17(2):158–175

    Article  Google Scholar 

  21. Martin D, Fowlkes C, Tal D, Malik J (2001) “A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics”. In: Computer Vision, 2001. ICCV 2001 Proceedings. Eighth IEEE International Conference on, vol. 2. IEEE, pp 416–423

  22. Monteiro F C, Campilho A (2008) “Watershed framework to region-based image segmentation”. In: in Pattern Recognition, 2008. ICPR 2008 19th International Conference on. IEEE, pp 1–4

  23. Mumford D, Shah J (1989) Optimal approximations by piecewise smooth functions and associated variational problems. Commun Pure Appl Math 42(5):577–685

    Article  MathSciNet  MATH  Google Scholar 

  24. Osher S, Sethian J A (1998) Fronts propagating with curvature dependent speed: Algorithms based on hamilton-jacobi formulations. J Comput Phys 79(1):12–49

    Article  MathSciNet  MATH  Google Scholar 

  25. Paragios N, Deriche R (2000) Geodesic active contours and level sets for the detection and tracking of moving objects. IEEE Trans Pattern Anal Mach Intell 22 (3):266–280

    Article  Google Scholar 

  26. Reddi S, Rudin S, Keshavan H (1984) An optimal multiple threshold scheme for image segmentation. IEEE Trans Syst Man Cybern 4:661–665

    Article  Google Scholar 

  27. Sapna Varshney S, Rajpa N, Purwar R (2009) “Comparative study of image segmentation techniques and object matching using segmentation”. In: in Methods and Models in Computer Science, 2009. ICM2CS 2009 Proceeding of International Conference on. IEEE, pp 1–6

  28. Sofou A, Maragos P (2008) Generalized flooding and multicue pde-based image segmentation. IEEE Trans Image Process 17(3):364–376

    Article  MathSciNet  Google Scholar 

  29. Tsai A, Yezzi JrA., Willsky A S (2001) Curve evolution implementation of the mumford-shah functional for image segmentation, denoising, interpolation, and magnification. IEEE Trans Image Process 10(8):1169–1186

    Article  MATH  Google Scholar 

  30. Vese L A, Chan T F (2002) A multiphase level set framework for image segmentation using the mumford and shah model. Int J Comput Vis 50(3):271–293

    Article  MATH  Google Scholar 

  31. Wang X -F, Huang D -S, Xu H (2010) An efficient local chan–vese model for image segmentation. Pattern Recogn 43(3):603–618

    Article  MATH  Google Scholar 

  32. Wang L, Li C, Sun Q, Xia D, Kao C -Y (2009) Active contours driven by local and global intensity fitting energy with application to brain mr image segmentation. Comput Med Imaging Graph 33(7):520– 531

    Article  Google Scholar 

  33. Wang L, Pan C (2014) Robust level set image segmentation via a local correntropy-based k-means clustering. Pattern Recogn 47(5):1917–1925

    Article  Google Scholar 

  34. Wang L, Yu Z, Pan C (2011) “Medical image segmentation based on novel local order energy”. In: Computer Vision–ACCV 2010. Springer, pp 148–159

  35. Xu C, Prince J (1998) Snakes, shapes, and gradient vector flow. IEEE Trans Image Process 7(3):359– 369

    Article  MathSciNet  MATH  Google Scholar 

  36. Yasmin M, Sharif M, Mohsin S (2013) Neural networks in medical imaging applications: a survey. World Applied Sciences Journal 22(1):85–96

    Google Scholar 

  37. Zhang K, Song H, Zhang L (2010) Active contours driven by local image fitting energy. Pattern Recogn 43(4):1199–1206

    Article  MATH  Google Scholar 

Download references

Acknowledgments

This research was supported by the National Natural Science Foundation of China (Grant No. 61440025 , 61402133) and the National Postdoctoral Science Foundation(Grant No. 20100480998)

Author information

Authors and Affiliations

  1. School of Computer Science and Technology, Harbin Institute of Technology, 92 West Dazhi Street, Nan Gang District, Harbin, 150001, People’s Republic of China

    Dansong Cheng, Daming Shi & Rui Wu

  2. School of Computer Science and Technology, Harbin Institute of Technology and School of Engineering, Harbin University, Harbin, People’s Republic of China

    Lin Liu

  3. Faculty of Science & Technology, Bournemouth University, Bournemouth, UK

    Feng Tian

Authors
  1. Lin Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Dansong Cheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Feng Tian
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Daming Shi
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Rui Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dansong Cheng.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, L., Cheng, D., Tian, F. et al. Active contour driven by multi-scale local binary fitting and Kullback-Leibler divergence for image segmentation. Multimed Tools Appl 76, 10149–10168 (2017). https://doi.org/10.1007/s11042-016-3603-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-016-3603-z

Keywords