Skip to main content

Advertisement

Springer Nature Link
Log in

Sparsity estimation based adaptive matching pursuit algorithm

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

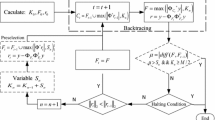
Compared with convex optimization algorithms and combination algorithms, greedy pursuit algorithms can balance operational efficiency and reconstruction precision, so they are widely used in the signal reconstruction step of compressed sensing. However, most existing greedy pursuit algorithms only work well if the signal sparsity is known, and their reconstruction performance is influenced by signal sparsity. To more accurately match the sparsity and obtain better reconstruction performance, we propose a greedy pursuit algorithm, the sparsity estimation based adaptive matching pursuit algorithm, which achieves image reconstruction using a signal sparsity estimation based on the Restricted Isometry Property (RIP) criterion and a flexible step size. Experimental results demonstrate that this algorithm provides better reconstruction performance and lower computation time, using different measurement matrices, when the sparsity is estimated in advance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Bin G, Sun X, Sheng VS (2016a) Structural minimax probability machine. IEEE Transactions on Neural Networks and Learning Systems. doi:10.1109/TNNLS.2016.2544779

    Google Scholar 

  2. Bin G, Victor S, Sheng A (2016b) Robust regularization path algorithm for ν-support vector classification. IEEE Transactions on Neural Networks and Learning Systems. doi:10.1109/TNNLS.2016.2527796

    Google Scholar 

  3. Blumensath T, Davies ME (2009) Stagewise Weak Gradient Pursuits. IEEE Trans Signal Process 57(11):4333–4346

    Article  MathSciNet  Google Scholar 

  4. Candès EJ (2006) Compressive sampling. In Proceedings of the International Congress of Mathematicians 3:1433–1452

    MathSciNet  MATH  Google Scholar 

  5. Candes E, Romberg J (2005) l1-magic: Recovery of sparse signals via convex programming. URL:www.acm.caltech.edu/l1magic/downloads/l1magic.pdf, 4, p 14

  6. Candes EJ, Romberg J, Tao T (2006) Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory 52(2):489–509

    Article  MathSciNet  MATH  Google Scholar 

  7. Dai W, Milenkovic O (2009) Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans Inf Theory 55(5):2230–2249

    Article  MathSciNet  MATH  Google Scholar 

  8. Daubechies I, Defrise M, De Mol C (2004) An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Comm Pure Appl Math 57:1413–1457

    Article  MathSciNet  MATH  Google Scholar 

  9. Do TT, Gan L, Nguyen N et al. (2008) Sparsity adaptive matching pursuit algorithm for practical compressed sensing. 42nd Asilomar IEEE Conference on Signals, Systems and Computers, p 581–587

  10. Donoho DL, Tsaig Y, Drori I et al. (2006) Sparse Solution of Underdetermined Linear Equations by Stagewise Orthogonal Matching Pursuit. Technique Report TR-2006-2, Standford University, Department of Statistics

  11. Donoho DL, Elad M, Temlyakov VN (2007) On Lebesgue-typ2e inequalities for greedy approximation. Journal of Approximation Theory 147(2):185–195

    Article  MathSciNet  MATH  Google Scholar 

  12. Elad M, Bruckstein AM (2002) A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Transactions on Information Theory, p 2558–2567

  13. Eldar YC., Kutyniok G eds. (2012) Compressed sensing: theory and applications. Cambridge University Press

  14. Figueiredo MAT, Nowak RD, Wright SJ (2007) Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems. IEEE J Sel Top Signa 1:586–597

    Article  Google Scholar 

  15. Fornasier M, Rauhut H (2010) Compressive sensing. Handbook. Mathematical Methods in Imaging, vol. 1, ed. by O. Scherzer Springer, Berlin, p 187–229

  16. Foucart S, Rauhut H (2013) Restricted Isometry Property. A Mathematical Introduction to Compressive Sensing. Springer, New York, 133–174

  17. Gilber AC, Strauss MJ, Tropp JA et al. (2006) Algorithmic linear dimension reduction in the L1 norm for sparse vectors. Proceedings of the 44th Annual Allerton Conference on Communication, Control and Computing 1–9

  18. Gilbert AC, Strauss MJ, Vershynin R (2007) One sketch for all: Fast algorithms for Compressed Sensing. In Proc. 39th ACM Symp. Theory of Computing (STOC), San Diego, June 2007

  19. Hoyer PO (2004) Non-negative matrix factorization with sparseness constraints. J Mach Learn Res 5:1457–1469

  20. Iwen MA (2010) Combinatorial sublinear-time Fourier algorithms. Found Comput Math 10(3):303–338

    Article  MathSciNet  MATH  Google Scholar 

  21. Jinming W, Xiao-Wen C (2017) The success probability of the Babai point estimator in box-constrained integer linear models. IEEE Trans Inf Theory 63:631–648

  22. Mallat SG, Zhang Z (1993) Matching pursuits with time-frequency dictionaries. IEEE Trans Signal Process 41(12):3397–3415

    Article  MATH  Google Scholar 

  23. Needell D, Tropp JA (2008) CoSaMP: iterative signal recovery from incomplete and inaccurate samples. Applied & computational Harmonic Analysis 26(12):93–100

    MathSciNet  MATH  Google Scholar 

  24. Needell D, Vershynin R (2010) Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit [J]. IEEE Journal of Selected Topics in Signal Processing 4(2):310–316

    Article  Google Scholar 

  25. Pan ZQ, Lei JJ, Zhang Y, Sun XM, Kwong S (2016a) Fast motion estimation based on content property for low-complexity H.265/HEVC encoder. IEEE Transactions on Broadcasting p 1–10 doi:10.1109/TBC.2016.2580920

  26. Pan Z, Lei J, Zhang Y et al (2016b) Fast motion estimation based on content property for low-complexity H. 265/HEVC encoder[J]. IEEE Trans Broadcast 62(3):675–684

    Article  Google Scholar 

  27. Sharon Y, Wright J, Ma Y (2007) Computation and Relaxation of Conditions for Equivalence between l1and l0 Minimization. CSL Technical Report UILU-ENG-07-2208, Univ. of Illinois, Urbana-Champaign

  28. Tropp JA, Gilbert AC (2007) Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Trans Inf Theory 53(12):4655–4666

    Article  MathSciNet  MATH  Google Scholar 

  29. Wang J, Kwon S, Shim B (2011a) Generalized orthogonal matching pursuit. IEEE Trans Signal Process 60(12):6202–6216

    Article  MathSciNet  Google Scholar 

  30. Wang H, Maldonado D, Silwal S (2011b) A nonparametric-test-based structural similarity measure for digital images. Comput Stat Data Anal 55(11):2925–2936

    Article  MathSciNet  Google Scholar 

  31. Xia Z, Wang X, Sun X et al (2014) Steganalysis of least significant bit matching using multi-order differences[J]. Security and Communication Networks 7(8):1283–1291

    Article  Google Scholar 

  32. Yao S, Wang T, Shen W, et al. (2015) Research of incoherence rotated chaotic measurement matrix in compressed sensing. Multimedia Tools & Applications 1–19

Download references

Acknowledgements

The research work reported in this paper is supported by the National Natural Science Foundation of China (No: 41271398, 41671382, 61572372), China Postdoctoral Science Foundation (Grant No.2016 M592409), National Program on Key Basic Research Project (No: 2011CB302306). In addition, this work is partially supported by LIESMARS Special Research Funding, SAST Funding (No. SAST201425) and Open Funding of NUIST, PAPD and CICAEET.

Author information

Authors and Affiliations

  1. Faculty of information engineering, China University of Geosciences, Wuhan, China

    Shihong Yao

  2. State Key Laboratory for Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan, China

    Tao Wang, Yanwen Chong & Shaoming Pan

  3. Collaborative Innovation Center for Geospatial Technology, Wuhan University, Wuhan, China

    Tao Wang

Authors
  1. Shihong Yao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Tao Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yanwen Chong
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Shaoming Pan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yanwen Chong.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yao, S., Wang, T., Chong, Y. et al. Sparsity estimation based adaptive matching pursuit algorithm. Multimed Tools Appl 77, 4095–4112 (2018). https://doi.org/10.1007/s11042-016-4295-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-016-4295-0

Keywords