Skip to main content
SpringerLink
Log in

A hybrid scheme for self-adaptive double color-image encryption

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

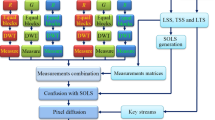
Most of existing optical color image encryption schemes have born security risks due to the adoption of linear transform, and data redundancy for the generation of complex image. To settle these problems effectively, a hybrid scheme for self-adaptive double color-image encryption is proposed in this paper. In this scheme, each RGB color component of two secret color images is first compressed and encrypted by 2-D compressive sensing (CS) in which measurement matrices are generated by 1-D compound chaotic systems and further are optimized by steepest descent algorithm to improve image reconstruction effect. Then, the two measured images are regarded as the real part and imaginary part to constitute a complex image, respectively. In the end, the complex image is reencrypted by self-adaptive random phase encoding and discrete fractional random transform (DFrRT) to obtain the final encrypted data. In the process of DFrRT and random phase encoding, the correlations between R, G, B components are adequately utilized. The production of key streams not only depends on the initial values of chaotic systems but also on plaintexts, and the three color components affect each other to enhance the ability against the known plaintext attack. The projection neural network algorithm is adopted to obtain the decryption images. Simulation results also verify the validity and security of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Baraniuk RG (2007) Compressive sensing. IEEE Signal Proc Mag 24(4)

  2. Candes EJ, Romberg JK, Tao T (2006) Stable signal recovery from incomplete and inaccurate measurements. Commun Pur Appl Math 59(8):1207–1223

    Article  MathSciNet  MATH  Google Scholar 

  3. Chen F, Wong K-W, Liao X-F, Xiang T (2014) Period distribution of generalized discrete Arnold cat map. Theor Comput Sci 552:13–25

    Article  MathSciNet  MATH  Google Scholar 

  4. Chen L, Zhao D (2006) Optical color image encryption by wavelength multiplexing and lensless Fresnel transform holograms. Opt Express 14(19):8552–8560

    Article  Google Scholar 

  5. Chen W, Quan C, Tay CJ (2009) Optical color image encryption based on Arnold transform and interference method. Optical Communications, pp 3680–3685

  6. Deepan B, Quan C, Wang Y (2014) Multiple-image encryption by space multiplexing based on compressive sensing and the double-random phase-encoding technique. Appl Opt 53(20):4539–4547

    Article  Google Scholar 

  7. Huang R, Rhee KH, Uchida S (2014) A parallel image encryption method based on compressive sensing. Multimed Tools Appl 72(1):71–93

    Article  Google Scholar 

  8. Huang X, Ye G (2014) An image encryption algorithm based on hyper-chaos and DNA sequence. Multimed Tools Appl 72(1):57–70

    Article  Google Scholar 

  9. Joshi M, Singh K (2007) Color image encryption and decryption using fractional Fourier transform. Opt Commun 279(1):35–42

    Article  Google Scholar 

  10. Liang Y, Liu G, Zhou N-R, Wu J (2015) Color image encryption combining a reality-preserving fractional DCT with chaotic mapping in HSI space. Multimedia Tools Application, pp 1–16

  11. Li C-J, Li C-D, Huang T-W (2011) Exponential stability of impulsive high-order Hopfield-type neural networks with delays and reaction-diffusion. Int J Comput Math 88(15):3150–3162

    Article  MathSciNet  MATH  Google Scholar 

  12. Li C-J, Yu X-H, Huang T-W, Guo C, He X (2016) A generalized Hopfield network for nonsmooth constrained convex optimization: Lie derivative approach. IEEE T Neur Net Lear 27(2):308–321

    Article  MathSciNet  Google Scholar 

  13. Li C-J, Yu X-H, Yu W-W, Huang T-W, Liu Z-W (2016) Distributed event-triggered scheme for economic dispatch in smart grids. IEEE T Ind Informat 12 (5):1775–1785

    Article  Google Scholar 

  14. Li C-J, Zhou X-J, Gao DY (2014) Stable trajectory of logistic map. Nonlinear Dynam 78(1):209–217

    Article  MathSciNet  MATH  Google Scholar 

  15. Li H, Wang Y (2011) Double-image encryption based on discrete fractional random transform and chaotic maps. Opt Laser Eng 49(7):753–757

    Article  Google Scholar 

  16. Lin Q, Wong K -W, Chen J (2013) An enhanced variable-length arithmetic coding and encryption scheme using chaotic maps. J Syst Softw 86(5):1384–1389

    Article  Google Scholar 

  17. Liu H, Xiao D, Zhang YS (2015) Securely compressive sensing using double random phase encoding. Optik 126(20):2663–2670

    Article  Google Scholar 

  18. Liu Q, Wang J (2016) L 1-Minimization algorithms for sparse signal reconstruction based on a projection neural network. IEEE T Neur Learn 27(3):698–707

    Article  Google Scholar 

  19. Liu X, Mei W, Du H (2014) Optical image encryption based on compressive sensing and chaos in the fractional Fourier domain. J Mod Opt 61(19):1570–1577

    Article  Google Scholar 

  20. Liu Z, Li Z, Liu W, Wang Y, Liu S (2013) Image encryption algorithm by using fractional Fourier transform and pixel scrambling operation based on double random phase encoding. Opt Laser Eng 51(1):8–14

    Article  Google Scholar 

  21. Liu Z, Liu S (2007) Double image encryption based on iterative fractional Fourier transform. Opt Commun 275(2):324–329

    Article  Google Scholar 

  22. Lui OY, Wong K-W, Chen J, Zhou J (2012) Chaos-based joint compression and encryption algorithm for generating variable length ciphertext. Appl Soft Comput 12(1):125–132

    Article  Google Scholar 

  23. Nishchal NK, Joseph J, Singh K (2004) Securing information using fractional Fourier transform in digital holography. Opt Commun 235(4):253–259

    Article  Google Scholar 

  24. Norouzi B, Seyedzadeh SM, Mirzakuchaki S, Mosavi MR (2015) A novel image encryption based on row-column, masking and main diffusion processes with hyper chaos. Multimed Tools Appl 74(3):781–811

    Article  Google Scholar 

  25. Rawat N, Kumar R, Lee BG (2014) Implementing compressive fractional Fourier transformation with iterative kernel steering regression in double random phase encoding. Optik-Int J Light Electron Opt 125(18):5414–5417

    Article  Google Scholar 

  26. Sato D (2015) Security evaluation for leakage of a fingerprint image from USB-based fingerprint authentication systems. Proc IEICE 115(117):39–44

    Google Scholar 

  27. Sui L, Lu H, Wang Z, Sun Q (2014) Double-image encryption using discrete fractional random transform and logistic maps. Opt Laser Eng 56:1–12

    Article  Google Scholar 

  28. Tao R, Lang J, Wang Y (2008) Optical image encryption based on the multiple-parameter fractional Fourier transform. Opt Lett 33(6):581–583

    Article  Google Scholar 

  29. Wen J, Li D, Zhu F (2015) Stable recovery of sparse signals via L p -minimization. Appl Comput Harmon A 38(1):161–176

    Article  MATH  Google Scholar 

  30. Wen J, Zhou Z, Wang J, Tang X-H, Qun M (2016) A sharp condition for exact support recovery of sparse signals with orthogonal matching pursuit. IEEE T Appl Supercon

  31. Wen J, Zhu X, Li D (2013) Improved bounds on restricted isometry constant for orthogonal matching pursuit. Electron Lett 49(23):1487–1489

    Article  Google Scholar 

  32. Zhang L, Liao X-F, Wang X (2005) An image encryption approach based on chaotic maps. Chaos Solition Fract 24(3):759–765

    Article  MathSciNet  MATH  Google Scholar 

  33. Zhang S, Gao T (2015) An image encryption scheme based on DNA coding and permutation of hyper-image. Multimed Tools Appl 2015:1–14

    Google Scholar 

  34. Zhang Y -S, Xiao D (2013) Double optical image encryption using discrete Chirikov standard map and chaos-based fractional random transform. Opt Laser Eng 51(4):472–480

    Article  Google Scholar 

  35. Zhang Y-S, Zhang L-Y, Zhou J, Liu L, Chen F, He X (2016) A review of compressive sensing in information security field. IEEE Access 4:2507–2519

    Article  Google Scholar 

  36. Zhang Y-S, Zhou J, Chen F, Zhang L-Y, Wong K-W, He X (2016) Embedding cryptographic features in compressive sensing. Neurocomputing 205:472–480

    Article  Google Scholar 

  37. Zhang Y, Zhang L-Y (2015) Exploiting random convolution and random subsampling for image encryption and compression. Electron Lett 51(20):1572–1574

    Article  Google Scholar 

  38. Zhou Y-C, Bao L, Chen C-L (2014) A new 1D chaotic system for image encryption. Signal Process 97:172–182

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported in part by the National Key Research and Development Program of China under Grant 2016 YFB0800601, in part by the National Nature Science Foundation of China under Grant 61472331, in part by the Talents of Science and Technology promote plan, Chongqing Science & Technology Commission.

Author information

Authors and Affiliations

  1. Chongqing Key Laboratory of Nonlinear Circuits and Intelligent Information Processing, College of Electronic and Information Engineering, Southwest University, Chongqing, 400715, China

    Fang Han, Xiaofeng Liao, Bo Yang & Yushu Zhang

Authors
  1. Fang Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaofeng Liao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bo Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yushu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaofeng Liao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Han, F., Liao, X., Yang, B. et al. A hybrid scheme for self-adaptive double color-image encryption. Multimed Tools Appl 77, 14285–14304 (2018). https://doi.org/10.1007/s11042-017-5029-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-017-5029-7

Keywords

Search

Navigation