Color and depth image registration algorithm based on multi-vector-fields constraints

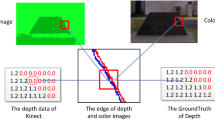
Abstract

Image registration, which aim to establish a reliable feature relationship between images, is a critical problem in the field of image processing. In order to enhance the accuracy of color and depth image registration, this paper proposes an novel image registration algorithm based on multi-vector-fields constraints. We first initialize the edge information features of color and depth images, and establish putative correspondences based on edge information. Consider the correlation between the images, establish the functional relationships of the multi-vector-fields constraints based on the relationships. In the reproducing nuclear Hilbert space (RKHS), this constraint is added to the probability model, and the model parameters are optimized using the EM algorithm. Finally, the probability of corresponding edge points of the image is obtained. In order to further improve registration accuracy, this paper will change the input from one pair to two pairs and let the feature transformation relationship between images be iteratively evaluated using the parameter model. Taking publicly available RGB-D images as experimental subjects, results show that for single object image registration, the algorithm image registration accuracy in this paper is improved by about 5% compared with SC, ICP, and CPD algorithms. In addition, artificial noise was used to test the proposed algorithm’s anti-noise ability, results show that the proposed algorithm has superior anti-noise ability relative to SC, ICP and CPD algorithms.

Appendix

1.1 A.1 Theoretical explanation of convergence

I have consulted a lot of relevant data, trying to prove that the algorithm is convergent theoretically. After many attempts, I realized that the core of the problem is to prove whether the objective function is a convex function.The main functions of the support computation model are:

$$ Q\left( f \right) = - \frac{1}{{2{\sigma^{2}}}} \sum \limits_{n = 1}^{N} {p_{n}}{\left\| {{y_{n}} - M({x_{n}})} \right\|^{2}} + \langle E^{1}C^{1},E^{3}C^{3} \rangle + \langle E^{2}C^{2},E^{4}C^{4} \rangle $$

(13)

Where f denotes the mapping relationship between four images, Q (f) denotes the parametric model about f, p_n denotes the posterior probability of the mixed model of the n th pair of registration points, and ∥y_n − M(x_n)∥² denotes the difference between the n th pair of initial input and the n th pair of target points after transformation,σ represents the standard deviation of Gauss probability model and belongs to the parameter. 〈f_k, f_k+ 2〉 is the inner product of functions in RHKS space. (that is the formula 10). If we can prove that the$- \frac {1}{{2{\sigma ^{2}}}} \sum \limits _{n = 1}^{N} {p_{n}}{\left \| {{y_{n}} - M({x_{n}})} \right \|^{2}}$ is convex, then we can solve the problem of convergence proof along the way of EM convergence proof.At the same time, because 〈f_k, f_k+ 2〉, under the conditions of this paper, can be converted to Gaussian radial basis function values, and negative exponential radial basis function in the independent variable greater than zero, the value of the function tends to zero.

Therefore, the key point is to prove that p_n∥y_n − M(x_n)∥² is a concave function (When multiplied by $- \frac {1}{{2{\sigma ^{2}}}}$, it becomes a convex function).Here is our proof:

First, for the polynomial ${\sum }_{n = 1}^{\infty }p_{n}\left \Vert Y_{n}-M(x_{n})\right \Vert ^{2}$, it can be regarded as an infinite series, where 0 <= p_n <= 1, 0 <= ∥Y_n − M(x_n)∥² <= distmax, (distmax represents the maximum distance between two points in the picture). Further, the inequality can be obtained:0 <= p_n ∥Y_n − M(x_n)∥²N₀ <= distmaxN₀ < L < 1,N₀ is a positive integer greater than zero, L is a constant satisfying the inequality. Obviously, N₀ exists.According to the root discriminant method, we know that series ${\sum }_{n = 1}^{\infty }p_{n}\left \Vert Y_{n}-M(x_{n})\right \Vert ^{2}$ must converge. Then, according to the Lazystatistician rule, we get the equation:

$$ {\sum}_{n = 1}^{N} p_{n}\left\Vert Y_{n}-M(x_{n})\right\Vert^{2}=E(\left\Vert Y_{n}-M(x_{n})\right\Vert^{2}); $$

(14)

where E represents expectation.

In functional analysis, for discrete variables, the two norm of a matrix is equal to the sum of the transformation of functions, that is: $\left \Vert Y_{n}-M(x_{n})\right \Vert ^{2}\Rightarrow \sum \limits _{n = 1}^{N}D(x_{n})^{2}$,where D(x₍n)) is a function equivalent expression of ∥Y_n − M(x_n)∥².

After that ,according to Hilbert kernel space property, any function in space can be represented by a base, $D(x_{n})={\sum }_{i = 1}^{N}D_{i}\sqrt {\lambda _{i}}\psi _{i},D_{i}$,where D(x_n) is the transformation of the i th component, λ_i is the corresponding constant of the i th transformation, and ψ_i is the kernel function. And the kernel function in this paper is ψ_i = exp(−β ∥x − x_i∥²), (β > 0),it’s a concave function,and because concave function adds or concave function, so the D(x_n) is a concave function, plus the minus sign of $- \frac {1}{{2{\sigma ^{2}}}}$, $- \frac {1}{{2{\sigma ^{2}}}} \sum \limits _{n = 1}^{N} {p_{n}}{\left \| {{y_{n}} - M({x_{n}})} \right \|^{2}}$ has the function property of convex function.

According to Jensen inequality, E(D(x_n)) >= D(E(x_n)),if and only if x₁ = x₂ = x₃ = ... = x_n obtains an equal sign. Therefore,

$-\sum \limits _{n = 1}^{N} {p_{n}}{\left \| {{y_{n}} - M({x_{n}})} \right \|^{2}}>=\sum \limits _{n = 1}^{N}p_{n}Y_{n}+\sum \limits _{n = 1}^{N}p_{n}M(x_{n})$.In the M-step of EM algorithm, the parameter maximization ensures that the lower bound $\sum \limits _{n = 1}^{N}p_{n}Y_{n}+\sum \limits _{n = 1}^{N}p_{n}M(x_{n})$ is greater than or equal to that before the iteration, so we can gradually approximate the convergence value of the objective function by raising the lower bound $\sum \limits _{n = 1}^{N}p_{n}Y_{n}+\sum \limits _{n = 1}^{N}p_{n}M(x_{n})$ iteratively.

Therefore, the objective function is convergent in theory.

1.2 A.2 Notation table

Table 3 is a supplement to the symbols of the formula, including the collection of main symbols.

Table 3 A notation table of main symbols