Abstract
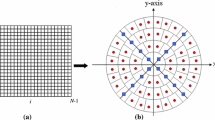
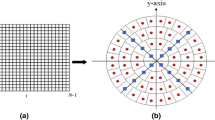
In this work, we suggest a new set of quaternion discrete radial Krawtchouk moments (QDRKMs) for color image reconstruction and classification. These new discrete moments are represented over a disk by using discrete orthogonal radial Krawtchouk moments. The use of Quaternion discrete moments for color image eliminates the discretization errors produced when the Quaternion continuous moments are used. Furthermore, this approach is suggested for highly accurate calculation of QDRKMs in polar coordinates where the kernel is exactly calculated by over circular color pixels. The translation, scaling, and rotation (TSR) invariances for QDRKMs are proved. Theoretical analysis and numerical experiments investigation were shown in terms of the performance description of TSR invariances, classification and robustness to different noises of the QDRKMs compared with continuous quaternion Legendre–Fourier moments using COIL 100 database.










Similar content being viewed by others
References
Amakdouf H, El Mallahi M, Zouhri A, Qjidaa H (2018) Classification and recognition of 3D image of charlier moments using a multilayer perceptron architecture. Procedia Computer Science 127(2018):226–235
Cao L, Zhi R, Jin Y (2018) Translation and scale invariants of krawtchouk moments. Inf Process Lett 130(C):30–35
Chen B, Shu H, Zhang H, Chen G, Luo L (2010) Color image analysis by quaternion zernike moments. In: Proceedings - international conference on pattern recognition
Chen BJ, Shu HZ, Zhang H, Chen G, Toumoulin C, Dillenseger JL, Luo LM (2012) Quaternion Zernike moments and their invariants for color image analysis and object recognition. Signal Process 92:308–318. https://doi.org/10.1016/j.sigpro.2011.07.018
Chen B, Shu H, Coatrieux G, Chen G, Sun X, Coatrieux JL (2014) Color image analysis by quaternion-type moments. J Math Imaging Vis
Chen B, Qi X, Sun X, Shi YQ (2017) Quaternion pseudo-Zernike moments combining both of RGB information and depth information for color image splicing detection. J Vis Commun Image Represent 49:283–290. https://doi.org/10.1016/j.jvcir.2017.08.011
El Mallahi M, Mesbah A, El Fadili H, Zenkouar K, and Qjidaa H. (2014) Compact computation of krawtchouk moments for 3D object representation. WSEAS transactions on circuits and systems E-ISSN: 2224-266X,13.
El Mallahi M, Mesbah A, El Fadili H, Zenkouar K, et H. Qjidaa. (2015) Translation and scale invariants of three-dimensional Krawtchouk moments, IEEE 2015 intelligent systems and computer vision, ISCV .
El Mallahi M, Mesbah A, Qjidaa H. (2016). “An algorithm for fast computation of 3D Krawtchouk moments for volumetric image reconstruction”, Proceedings of the Mediterranean Conference on Information & Communication Technologies 2015 pp 267-276
El Mallahi M, Mesbah A, El Fadili H, Zenkouar K, et Qjidaa H (2016) “Volumetric image reconstruction by 3D hahn moments.” 2015 ieee/acs 12th international conference of computer systems and applications (AICCSA).
El Mallahi M, Mesbah A, Qjidaa H (2016) “Fast algorithm for 3D local feature extraction using Hahn and Charlier moments” advances in ubiquitous networking 2, Lecture notes in electrical engineering, vol 397. Springer, Singapore
El Mallahi M, Zouhri A, EL-mekkaoui J, Qjidaa H (2017) Three dimensional radial Krawtchouk moment invariants for volumetric image recognition. Pattern Recognit Image Anal 27(4):810–824
El Mallahi, M. et al. (2017) ‘Three dimensional radial tchebichef moment invariants for volumetric image recognition’, Pattern Recognition and Image Analysis
El Mallahi M, Zouhri A, Mekkaoui J and Qjidaa H (2017) “Radial Meixner moments for rotational invariant pattern recognition”, IEEE 2017 intelligent systems and computer vision, ISCV .
El Mallahi, M. et al. (2017) Radial charlier moment invariants for 2D object/image recognition, in international conference on multimedia computing and systems -proceedings
El Mallahi M, Zouhri A, Amakdouf H, Qjidaa H (2018) Rotation scaling and translation invariants of 3D radial shifted Legendre moments. Springer, International Journal of Automation and Computing, Springer, April 2018 15(2):169–180
M. El Mallahi, A. Mesbah, et H. Qjidaa. (2018).“3D radial invariant of dual hahn moments.” Springer, Neural Computing and Applications. , Vol. 30, Issue 7, pp 2283–22.
El Mallahi M, Zouhri A, Mesbah A, El Affar I, Qjidaa H (2018) Radial invariant of 2D and 3D Racah moments. Springer, Multimedia Tools and Applications An International Journal 77(6):6583–6604
Mesbah A, El Mallahi M, Qjidaa H (2016) “Fast and efficient computation of three-dimensional Hahn moments” SPIE. Journal of electronic imaging 25(6):061621
Mesbah A, Zouhri A, El Mallahi M, Qjidaa H. (2017).“Robust reconstruction and generalized dual hahn moments invariants extraction for 3d images” spriger, 3D Research Center, Kwangwoon University and Springer-Verlag Berlin Heidelberg, vol. 8, num. 7, Issues 29
Mukundan, R. (2012) ‘A comparative analysis of radial-Tchebichef moments and Zernike moments’, in. doi: https://doi.org/10.5244/c.23.16.
Wang XY, Li WY, Yang HY, Wang P, Li YW (2015) Quaternion polar complex exponential transform for invariant color image description. Appl Math Comput 256:951–967. https://doi.org/10.1016/j.amc.2015.01.075
Xiang-Yang W, Wei-Yi L, Hong-Ying Y, Pan-Pan N, Yong-Wei L (2015) Invariant quaternion radial harmonic Fourier moments for color image retrieval. Opt Laser Technol 66:78–88. https://doi.org/10.1016/j.optlastec.2014.07.020
Xiao B, Ma JF, Cui JT (2012) Radial Tchebichef moment invariants for image recognition. J Vis Commun Image Represent 23:381–386
Xiao B, Wang GY, and Li WS (2014) Radial shifted legendre moments for image analysis and invariant image recognition Image Vis. Comput.
Xiao B, Zhang Y, Li L, Weisheng L, Wang G (2016) Explicit Krawtchouk moment invariants for invariant image recognition. J Electron Imaging 25(2):023002
Acknowledgements
I would like to express my deep gratitude to Dr. Amal Zouhri, for her advice and assistance in keeping my progress on schedule. I would also like to thank Professor Mostafa EL MALLAHI and Professor Hassan Qjidaa, my research supervisors, for their patient guidance, enthusiastic encouragement and useful critiques of this research work. Finally, I wish to thank my parents for their support and encouragement throughout my study.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Amakdouf, H., Zouhri, A., EL Mallahi, M. et al. Color image analysis of quaternion discrete radial Krawtchouk moments. Multimed Tools Appl 79, 26571–26586 (2020). https://doi.org/10.1007/s11042-020-09120-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11042-020-09120-0