Skip to main content
Springer Nature Link
Log in

Robust cryptosystem using a new hyperchaotic oscillator with stricking dynamic properties

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

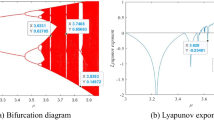
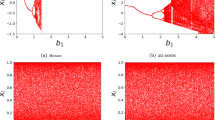
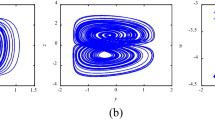
This paper presents a digital image cryptosystem utilizing a novel dynamic system with very interesting features. The oscillator is designed by introducing a feedback control law to the third line of the Lorenz oscillator with exponential nonlinearity. This exponential nonlinearity is replaced with hyperbolic sine nonlinearity to induce more complexity in the oscillator. Using some well-known computation analysis tools like Lyapunov spectrum, bifurcation analysis, and phase portraits representations, the dynamic analysis indicates that the oscillator can show chaos or hyperchaos for the same parameter space. In addition, the oscillator is equilibrium free, consequently its attractors are classified as hidden. Finally, the sequences of the oscillator are utilized to design a robust encryption scheme. Our method relies on a discrete orthogonal moment, confusion and diffusion stages. The input image is represented in the transform domain using Hahn orthogonal moments. Chaotic sequences are used to confuse and diffuse the obtaind image. Various security techniques have been used with success to show that our encryption process is powerful to resist malicious attacks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. ABD El-Latif AA, Li L, Wang N, Han Q, Niu X (2013) A new approach to chaotic image encryption based on quantum chaotic system, exploiting color spaces. Signal Process 93(11):2986–3000

    Article  Google Scholar 

  2. Abbas NA (2016) Image encryption based on independent component analysis and arnold’s cat map. Egyptian Informatics Journal 17(1):139–146

    Article  Google Scholar 

  3. Abd El-Latif AA, Abd-El-Atty B, Mazurczyk W, Fung C, Venegas-Andraca SE (2020) Secure data encryption based on quantum walks for 5g internet of things scenario. IEEE Trans Netw Serv Manag 17(1):118–131

    Article  Google Scholar 

  4. Ahmad J, Khan MA, Ahmed F, Khan JS (2018) A novel image encryption scheme based on orthogonal matrix, skew tent map, and xor operation. Neural Comput Appl 30(12):3847–3857

    Article  Google Scholar 

  5. Ahmed HEDH, Kalash HM, Allah OF (2007) Encryption efficiency analysis and security evaluation of rc6 block cipher for digital images. In: 2007 International conference on electrical engineering. IEEE, pp 1–7

  6. Alvarez G, Li S (2003) Cryptographic requirements for chaotic secure communications, arXiv:nlin/0311039

  7. Auyporn W, Vongpradhip S (2015) A robust image encryption method based on bit plane decomposition and multiple chaotic maps. Int J Signal Process Syst 3(1):8–13

    Google Scholar 

  8. Bao B, Hu F, Chen M, Xu Q, Yu Y (2015) Self-excited and hidden attractors found simultaneously in a modified Chua’s circuit. International Journal of Bifurcation and Chaos 25(05):1550075

    Article  MATH  Google Scholar 

  9. Belazi A, Hermassi H, Rhouma R, Belghith S (2014) Algebraic analysis of a rgb image encryption algorithm based on dna encoding and chaotic map. Nonlinear Dyn 76(4):1989–2004

    Article  MATH  Google Scholar 

  10. Brucoli M, Carnimeo L, Grassi G (1996) A method for the synchronization of hyperchaotic circuits. International Journal of Bifurcation and Chaos 6 (09):1673–1681

    Article  MATH  Google Scholar 

  11. El Fishawy NF, Zaid OMA (2007) Quality of encryption measurement of bitmap images with rc6, mrc6, and Rijndael block cipher algorithms. IJ Network Security 5(3):241–251

    Google Scholar 

  12. El-Ashry I (2010) Digital image encryption, MS. c Thesis, Electronics and Electrical Communications Engineering Department, Faculty of Electronic Engineering, Menofia University

  13. Elkamchouchi H, Makar M (2005) Measuring encryption quality for bitmap images encrypted with Rijndael and Kamkar block ciphers. In: Proceedings of the twenty-second national radio science conference, 2005. NRSC 2005. IEEE, pp 277–284

  14. Farah MB, Guesmi R, Kachouri A, Samet M (2020) A novel chaos based optical image encryption using fractional fourier transform and dna sequence operation. Opt Laser Technol 121:105777

    Article  MATH  Google Scholar 

  15. Gao T, Chen Z (2008) A new image encryption algorithm based on hyper-chaos. Phys Lett A 372(4):394–400

    Article  MATH  Google Scholar 

  16. JZhou J, Shu H, Zhu H, Toumoulin C, Luo L (2005) Image analysis by discrete orthogonal hahn moments. In: International conference image analysis and recognition. Springer, pp 524–531

  17. Jithin K, Sankar S (2020) Colour image encryption algorithm combining, arnold map, dna sequence operation, and a mandelbrot set. J Inf Secur Appl 50:102428

    Google Scholar 

  18. Kapitaniak T (1994) Synchronization of chaos using continuous control. Phys Rev E 50(2):1642

    Article  Google Scholar 

  19. Kengne J, Tsafack N, Kengne LK (2018) Dynamical analysis of a novel single opamp-based autonomous lc oscillator: antimonotonicity, chaos, and multiple attractors. Int J Dyn Control 6(4):1543– 1557

    Article  MathSciNet  Google Scholar 

  20. Khan JS, Ahmad J (2019) Chaos based efficient selective image encryption. Multidim Syst Sign Process 30(2):943–961

    Article  MathSciNet  MATH  Google Scholar 

  21. Leutcho G, Kengne J, Kengne LK (2018) Dynamical analysis of a novel autonomous 4-d hyperjerk circuit with hyperbolic sine nonlinearity: Chaos, antimonotonicity and a plethora of coexisting attractors. Chaos, Solitons & Fractals 107:67–87

    Article  MathSciNet  MATH  Google Scholar 

  22. Li Y, Chen G, Tang WKS (2005) Controlling a unified chaotic system to hyperchaotic. IEEE Trans Circuits Syst II: Express Briefs 52(4):204–207

    Article  Google Scholar 

  23. Li Y, Tang WK, Chen G (2005) Hyperchaos evolved from the generalized lorenz equation. Int J Circuit Theor Appl 33(4):235–251

    Article  MATH  Google Scholar 

  24. Lian S (2008) Multimedia content encryption: techniques and applications. CRC Press, Boca Raton

    Book  MATH  Google Scholar 

  25. Liang J, Shi Z (2004) The information entropy, rough entropy and knowledge granulation in rough set theory. International journal of uncertainty, fuzziness and knowledge-based systems 12(01):37–46

    Article  MathSciNet  MATH  Google Scholar 

  26. Liu Y, Jiang Z, Xu X, Zhang F, Xu J (2020) Optical image encryption algorithm based on hyper-chaos and public-key cryptography. Opt Laser Technol 127:106171

    Article  Google Scholar 

  27. Liu H, Kadir A (2015) Asymmetric color image encryption scheme using 2d discrete-time map. Signal Process 113:104–112

    Article  Google Scholar 

  28. Lorenz EN (1969) The predictability of a flow which possesses many scales of motion. Tellus 21(3):289–307

    Article  Google Scholar 

  29. Luo Y, Zhou R, Liu J, Cao Y, Ding X (2018) A parallel image encryption algorithm based on the piecewise linear chaotic map and hyper-chaotic map. Nonlinear Dynamics 93(3):1165–1181

    Article  Google Scholar 

  30. Matthews R (1989) On the derivation of a “chaotic” encryption algorithm. Cryptologia 13(1):29–42

    Article  MathSciNet  Google Scholar 

  31. Murali K, Lindberg E, Leung H (2002) Design principles of hyperchaotic circuits. In: AIP Conference proceedings, vol 622. American Institute of Physics, pp 15–26

  32. Negou AN, Kengne J (2018) Dynamic analysis of a unique jerk system with a smoothly adjustable symmetry and nonlinearity: Reversals of period doubling, offset boosting and coexisting bifurcations. AEU-Int J Electron C 90:1–19

    Article  Google Scholar 

  33. Njitacke ZT, Isaac SD, Tsafack N, Kengne J (2020) Window of multistability and its control in a simple 3d hopfield neural network: application to biomedical image encryption. Neural Comput and Applic: 1–20

  34. Nkapkop JDD, Effa JY, Borda M, Bitjoka L, AMohamadou A (2017) Chaotic encryption scheme based on a fast permutation and diffusion structure. Int Arab J Inf Technol 14(6):812–819

    Google Scholar 

  35. Nkapkop JDD, Effa JY, Borda M, Terebes R (2015) A novel fast and secure chaos-based algorithm for image encryption. In: International conference for information technology and communications. Springer, pp 87–101

  36. Rossler O (1979) An equation for hyperchaos. Phys Lett A 71 (2-3):155–157

    Article  MathSciNet  MATH  Google Scholar 

  37. Signing VF, Kengne J (2018) Coexistence of hidden attractors, 2-torus and 3-torus in a new simple 4-d chaotic system with hyperbolic cosine nonlinearity. Int J Dyn Control 6(4):1421–1428

    Article  MathSciNet  Google Scholar 

  38. Sivakumar T, Li P (2019) A secure image encryption method using scan pattern and random key stream derived from laser chaos. Opt Laser Technol 111:196–204

    Article  Google Scholar 

  39. Tsafack N, Kengne J (2018) A novel autonomous 5-d hyperjerk rc circuit with hyperbolic sine function. The Scientific World Journal

  40. Tsafack N, Kengne J (2019) Complex dynamics of the chua’s circuit system with adjustable symmetry and nonlinearity: Multistability and simple circuit realization. World 4(2):24–34

    Google Scholar 

  41. Tsafack N, Kengne J, BAbd-El-Atty B, Iliyasu AM, Hirota K, Abd EL-Latif AA (2020) Design and implementation of a simple dynamical 4-d chaotic circuit with applications in image encryption. Inform Sci 515:191–217

    Article  MATH  Google Scholar 

  42. Tsafack N, Nkapkop JDD, Jacques K, Yves EJ, Iliyasu AM, Abd El-Latif AA (2020) A multidimensional hyperjerk oscillator: Dynamics analysis, analogue and embedded systems implementation, and its application as a cryptosystem. Sensors 20(1):83

    Google Scholar 

  43. Tsafack N, Sankar S, Abd-El-Atty B, Kengne J, Jithin K, Belazi A, Mehmood I, Bashir AK, Song OY, Abd El-Latif AA (2020) A new chaotic map with dynamic analysis and encryption application in internet of health things. IEEE Access 8:137731–137744

    Article  Google Scholar 

  44. Wang X, Zhao H, Wang Y (2019) A new image encryption algorithm with nonlinear-diffusion based on multiple coupled map lattices. Opt Laser Technol 115:42–57

    Article  Google Scholar 

  45. Wei W, Yang Q (2011) Dynamical analysis of a new autonomous 3-d chaotic system only with stable equilibria. Nonlinear Anal Real World Appl 12 (1):106–118

    Article  MathSciNet  MATH  Google Scholar 

  46. Wei Z, Zhang W (2014) Hidden hyperchaotic attractors in a modified lorenz–stenflo system with only one stable equilibrium. International Journal of Bifurcation and Chaos 24(10):1450127

    Article  MathSciNet  MATH  Google Scholar 

  47. Wu J, Luo X, Zhou N (2013) Four-image encryption method based on spectrum truncation, chaos and the modfrft. Opt Laser Technol 45:571–577

    Article  Google Scholar 

  48. Xu L, Gou X, Li Z, Li L (2017) A novel chaotic image encryption algorithm using block scrambling and dynamic index based diffusion. Opt Lasers Eng 91:41–52

    Article  Google Scholar 

  49. Zhu C, Wang G, Sun K (2018) Cryptanalysis and improvement on an image encryption algorithm design using a novel chaos based s-box. Symmetry 10(9):399

    Article  Google Scholar 

  50. Zhu S, Zhu C (2018) Image encryption algorithm with an avalanche effect based on a six-dimensional discrete chaotic system. Multimed Tools Appl 77 (21):29119–29142

    Article  Google Scholar 

Download references

Acknowledgements

TSAFACK Nestor is grateful to Prof. KENGNE Jacques for his inestimable broad knowledge, common sense, and ability to analyze intricate problems crucial to the success of this research work.

Author information

Authors and Affiliations

  1. Department of Physics, University of Ngaoundéré, P.O. Box 454, Ngaoundere, Cameroon

    Franklin Djimasra & Joseph Yves Effa

  2. Department of Electrical Engineering and Industrial Computing, University Institute of Technology, P.O. Box 8698, Douala, Cameroon

    Jean De Dieu Nkapkop

  3. Research Unit of Laboratory of Condensed Matter, Electronics and Signal Processing (URMACETS) Department of Physics, Faculty of Sciences, University of Dschang, P.O. Box 67, Dschang, Cameroon

    Nestor Tsafack

  4. Research Unit of Laboratory of Automation and Applied Computer (LAIA), Electrical Engineering Department of IUT-FV, University of Dschang, P.O. Box 134, Bandjoun, Cameroon

    Jacques Kengne

  5. Department of Electronics, University of MSB, Jijel, Algeria

    Abdelkrim Boukabou

  6. Department of Electrical Engineering, Energetics and Automatics, University of Ngaoundéré, Ngaoundéré, Cameroon

    Laurent Bitjoka

Authors
  1. Franklin Djimasra
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jean De Dieu Nkapkop
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Nestor Tsafack
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jacques Kengne
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Joseph Yves Effa
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Abdelkrim Boukabou
    View author publications

    You can also search for this author inPubMed Google Scholar

  7. Laurent Bitjoka
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Nestor Tsafack.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Djimasra, F., Nkapkop, J.D.D., Tsafack, N. et al. Robust cryptosystem using a new hyperchaotic oscillator with stricking dynamic properties. Multimed Tools Appl 80, 25121–25137 (2021). https://doi.org/10.1007/s11042-021-10734-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-021-10734-1

Keywords