Skip to main content
SpringerLink
Log in

Robust \(H_{\infty }\) deconvolution filtering of 2-D digital systems of orthogonal local descriptor

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

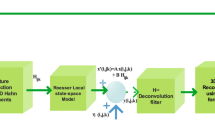
In this work, we propose a new set of \(H_{\infty }\) deconvolution filtering of 2-D color image using feature extraction of local descriptor and Fornasini-Machesini II (FM-II) model. The principal goal is to design 2-D deconvolution filter to reconstruct the noisy color image with the minimal information extracted from local Krawtchouk moment, Moreover, the filtering error system is asymptotically stable and satisfy the \(H_{\infty }\) performance index. the sufficient condition is given to ensure the \(H_{\infty }\) performance of the filtering error system through the Lyapunov theory, and the local Krawtckouk moment to give the feature extraction according to the order defined in advance instead of the global color image. Moreover, the 2-D deconvolution filter is designed to achieve the \(H_{\infty }\) performance index which the filter parameters are determined with certain optimization resolution. Finally, simulation example is provided to demonstrate the usefulness of the proposed design methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Amakdouf H, Zouhri A, EL Mallahi M et al (2020) Color image analysis of quaternion discrete radial Krawtchouk moments. Multimed Tools Appl 79:26571–26586. https://doi.org/10.1007/s11042-020-09120-0

    Article  Google Scholar 

  2. Amakdouf H, Zouhri A, El Mallahi M et al (2020) Artificial intelligent classification of biomedical color image using quaternion discrete radial Tchebichef moments. Multimed Tools Appl. https://doi.org/10.1007/s11042-020-09781-x

  3. Benzaouia A, El Younsi L, El Hajjaji A (2019) Stability and stabilization analysis for T–S interconnected fuzzy systems using LMIs. Circ Syst Signal Process 38:4504–4525. https://doi.org/10.1007/s00034-019-01082-5

    Article  Google Scholar 

  4. Boukili B, Hmamed A, Benzaouia A, EL Hajjaji A (2014) \(H_{\infty }\) filtering of two-dimensional T-S fuzzy system. Circ Syst Signal Process. https://doi.org/10.1007/s00034-013-9720-2

  5. Boukili B, Hmamed A, Tadeo F (2016) Reduced-order \(H_{\infty }\) filtering with intermittent measurements for a class of 2D systems. J Control Autom Electr Syst. https://doi.org/10.1007/s40313-016-0271-1

  6. Boukili B, Hmamed A, Tadeo F (2016) Robust \(H_{\infty }\) filtering for 2-D discrete Roesser systems. J Control Autom Electr Syst. https://doi.org/10.1007/s40313-016-0251-5

  7. Chen SF, Fong IK (2006) Robust \(H_{\infty }\) filtering for 2-D state-delayed systems with NFT uncertainties. IEEE Trans Signal Process 54(1):274–285

    Article  Google Scholar 

  8. Chen BS, Peng SC (1991) Optimal deconvolution filter design based on orthogonal principle. Signal Process 25:361–372

    Article  Google Scholar 

  9. Chucu L, Mosca E (1994) MMSE deconvolution via polynomial methods and its dual LQG regulation. Automatica 30:1197–1201

    Article  MathSciNet  Google Scholar 

  10. Cui JR, Hu GD (2010) State estimation of 2-D stochastic systems represented by FM-II model. Acta Autom Sin 36(5):755–761. https://doi.org/10.1016/S1874-1029(09)60034-3

    Article  MathSciNet  Google Scholar 

  11. Dami L, Benhayoun M, Benzaouia A (2020) Admissibility and stabilization of singular continuous 2D systems described by Roesser model. Multidimen Syst Sign Process 31:673–687. https://doi.org/10.1007/s11045-019-00681-4

    Article  MathSciNet  Google Scholar 

  12. Ding DW, Du X, Li X (2015) Finite-frequency model reduction of two-dimensional digital filters. IEEE Trans Autom Control 60(6):1624–1629

    Article  MathSciNet  Google Scholar 

  13. Du C, Xie L, Soh YC (2000) \(H_{\infty }\) filtering of 2-D discrete systems. IEEE Trans Signal Process 48(6):1760–1768

    Article  Google Scholar 

  14. El-Amrani A, Boukili B, Hmamed A, El Hajjaji A, Boumhidi I (2018) Robust \(H_{\infty }\) filtering for 2D continuous systems with finite frequency specifications. Int J Syst Sci. https://doi.org/10.1080/00207721.2017.1391960

  15. El Mallahi M, Zouhri A, El-Mekkaoui J et al (2017) Three dimensional radial Tchebichef moment invariants for volumetric image recognition. Pattern Recognit. Image Anal 27:810–824. https://doi.org/10.1134/S1054661817040113

    Google Scholar 

  16. El Mallahi M, Zouhri A, Amakdouf H, Qjidaa H (2018) Rotation scaling and translation invariants of 3D radial shifted legendre moments. Springer, Int J Autom Comput 15(2):169–180. Springer

    Article  Google Scholar 

  17. El Mallahi M, Mesbah A, Qjidaa H (2018) 3D radial invariant of dual Hahn moments. Neural Comput Appl 30(7):2283–22. Springer

    Article  Google Scholar 

  18. El Mallahi M, Zouhri A, Mesbah A et al (2018) Radial invariant of 2D and 3D Racah moments. Multimed Tools Appl 77:6583–6604. https://doi.org/10.1007/s11042-017-4573-5

    Article  Google Scholar 

  19. El Mallahi M, Zouhri A, Mesbah A, El Affar I, Qjidaa H (2018) Radial invariant of 2D and 3D Racah moments. Multimed Tools Appl Int J 77 (6):6583–6604. Springer

    Article  Google Scholar 

  20. Gao H, Lam J, Wang C, Xu S (2005) \(H_{\infty }\) model reduction for uncertain two-dimensional discrete systems. Optim Control Appl Methods 26:199–227

    Article  MathSciNet  Google Scholar 

  21. Kaczorek T (2009) LMI approach to stability of 2D positive systems. Multidim Syst Sign Process 20:39–54. https://doi.org/10.1007/s11045-008-0050-7

    Article  MathSciNet  Google Scholar 

  22. Kririm S, Hmamed A, Tadeo F (2015) Robust \(H_{\infty }\) filtering for uncertain 2D singular Roesser models. Circ Syst Signal Process 34 (7):2213–2235. https://doi.org/10.1007/s00034-015-9967-x

    Article  MathSciNet  Google Scholar 

  23. Lacerda MJ, Oliveira RCLF, Peres PLD (2011) Robust H2 and \(H_{\infty }\) Filter Design for uncertain linear systems via LMIs and polynomial matrices. Signal Process 91:1115–1122

    Article  Google Scholar 

  24. Mesbah A, Zouhri A, El Mallahi M, Qjidaa H (2017) Robust Reconstruction and Generalized Dual Hahn Moments Invariants Extraction for 3D Images. Springer, 3D Research Center, Kwangwoon University and Springer, Berlin. 18(7), Issues 29

    Book  Google Scholar 

  25. Nathan R (1966) Digital video handling. Jet Propulsion Lab., Pasadena, Tech. Rep. 32-877

  26. Rajan S, Joo KS, Bose T (1996) Analysis of 2-D state-space periodi-cally shift-variant discrete systems. Circuits Syst Signal Process 15(3):395–413

    Article  Google Scholar 

  27. Souza CE, Xie L, Coutinho DF (2010) Robust filtering for 2-D discrete-time linear systems with convex-bounded parameter uncertainty. Automatica 46:673–681

    Article  MathSciNet  Google Scholar 

  28. Wei G, Wang Z, Shu H, Fang G (2007) \(H_{\infty }\) deconvolution filter for stochastic systems with interval uncertainties. Circ Syst Signal Process 26(4):495–512. https://doi.org/10.1007/s00034-007-4004-x

    Article  MathSciNet  Google Scholar 

  29. Wu L, Shi P, Gao H, Wang C (2008) \(H_{\infty }\) filtering for 2D Markovian jump systems. Automatica 44(7):1849–1858

    Article  MathSciNet  Google Scholar 

  30. Xiao B, Ma JF, Cui JT (2012) Radial Tchebichef moment invariants for image recognition. J Vis Commun Image Represent 23(2):381–386. https://doi.org/10.1016/j.jvcir.2011.11.008

    Article  Google Scholar 

  31. Xiao B, Zhang YH, Li LP, Li WS, Wang G (2016) Explicit Krawtchouk moment invariants for invariant image recognition. J Electron Imaging 25 (2):Article number 023002. https://doi.org/10.1117/1.JEI.25.2

    Article  Google Scholar 

  32. Xie L, Wang S, Du C, Zhang C (2000) Hdeconvolution of periodic channels. Signal Process 80:2365–2378

    Article  Google Scholar 

  33. Xie L, Du C, Zhang C, Soh YC (2002) \(H_{\infty }\) deconvolution filtering of 2-D digital systems. IEEE Trans Signal Process 50(9):2319–2332

    Article  MathSciNet  Google Scholar 

  34. Xu S, Lam J, Zou Y, Lin Z, Paszke W (2005) Robust \(H_{\infty }\) filtering for uncertain 2-D continuous systems. IEEE Trans Signal Process 53 (5):1731–1738

    Article  MathSciNet  Google Scholar 

  35. Zhang B, Lam J, Xu S (2009) Deconvolution filtering for stochastic systems via homogeneous polynomial Lyapunov function. Signal Process 89:605–614

    Article  Google Scholar 

  36. Zouhri A, Amakdouf H, El Mallahi M et al (2020) Invariant Gaussian–Hermite moments based neural networks for 3D object classification. Pattern Recognit Image Anal 30:87–96. https://doi.org/10.1134/S1054661820010186

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. High Normal School, Department of Mathematics and Computer Sciences, Laboratory of Computer Sciences and Interdisciplinary Physics, Sidi Mohamed Ben Abdellah University, Fez, Morocco

    Mostafa El Mallahi

  2. Faculty of Sciences Dhar El Mahraz, Department of physics, Computer Science, Signals, Automation and Cognitivism Laboratory, Sidi Mohamed Ben Abdellah University, Fez, Morocco

    Bensalem Boukili, Amal Zouhri, Abdelaziz Hmamed & Hassan Qjidaa

Authors
  1. Mostafa El Mallahi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bensalem Boukili
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Amal Zouhri
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Abdelaziz Hmamed
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hassan Qjidaa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mostafa El Mallahi.

Ethics declarations

Conflict of Interests

The authors declare that they have no conflict of interest.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

El Mallahi, M., Boukili, B., Zouhri, A. et al. Robust \(H_{\infty }\) deconvolution filtering of 2-D digital systems of orthogonal local descriptor. Multimed Tools Appl 80, 25965–25983 (2021). https://doi.org/10.1007/s11042-021-10845-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-021-10845-9

Keywords

Search

Navigation